Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 78

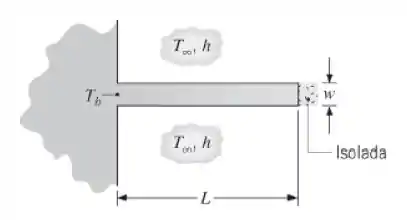
Uma aleta plana com seção transversal uniforme é feita com um material de condutividade térmica igual a 50 W m K , tem espessura w = 6 mm e comprimento de L = 48 mm, e é muito grande na direção normal à página. O coeficiente de transferência de calor por convecção é de 500 W m 2 K com uma temperatura do ar ambiente T ∞   =   30 ° C . A base da aleta é mantida a T b   =   100 ° C , enquanto a sua extremidade encontra-se isolada.

  1. Usando um método de diferenças finitas com um incremento espacial de 4 mm, estime a distribuição de temperaturas no interior da aleta. A hipótese de transferência de calor unidimensional é razoável para essa aleta?
  2. Estime a taxa de transferência de calor na aleta, por unidade de comprimento normal à página. Compare o seu resultado com o obtido utilizando a solução analítica para sistemas unidimensionais, Equação 3.81.
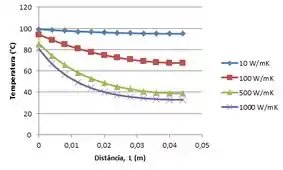
  3. Usando a malha de diferenças finitas da parte (a), calcule e represente graficamente a distribuição de temperaturas na aleta para valores de h   =   10 ,   100 ,   500   e   1000 W m 2 K . Determine e represente graficamente a taxa de transferência de calor na aleta em função de h.

Passo 1

Vamos pra mais umaaaa !!!

Preparados ?!

Na letra (a) nós vamos trabalhar com um incremento espacial de 4 mm, e assim estimar a distribuição de temperaturas no interior da aleta

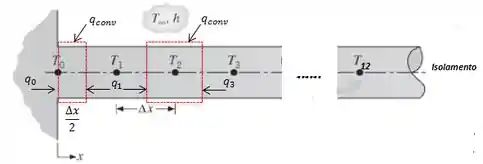
Nós já sabemos que:

T b   = T 0 =   100 ° C

T ∞ = 30 ° C

Bom galerinha, o Pontos 1 até 11 nós temos convecção e calor por condução que vem de dois pontos vizinhos:

2 + h P k A c ∆ x 2 T n = T n - 1 + T n + 1 + h P k A c ∆ x 2 T ∞

Se:

P = 2 l

A c = w l

Então:

2 l h k w l ∆ x 2 = 2 h k w ∆ x 2 = 2 500 W m 2 K 50 W m K 6 × 10 - 3   m 4 × 10 - 3   m 2 = 0,0533

Para o Ponto 1:

2,05333 T 1 = 100 ° C + T 2 + 0,0533 × 30 ° C

2,05333 T 1 = 101,6 + T 2

Para os Pontos 2 até 11 nós temos algo bem parecido:

2,05333 T 2 = T 1 + T 3 + 1,6

2,05333 T 3 = T 2 + T 4 + 1,6

2,05333 T 4 = T 3 + T 5 + 1,6

2,05333 T 5 = T 4 + T 6 + 1,6

2,05333 T 6 = T 5 + T 7 + 1,6

2,05333 T 7 = T 6 + T 8 + 1,6

2,05333 T 8 = T 7 + T 9 + 1,6

2,05333 T 9 = T 8 + T 10 + 1,6

2,05333 T 10 = T 9 + T 11 + 1,6

2,05333 T 11 = T 10 + T 12 + 1,6

Para os Pontos 12 nós temos calor vindo só do Ponto 11, e nossa equação ficará assim:

1 + h P k A c ∆ x 2 2 T n = T n - 1 + 2 h k w   ∆ x 2 2   T ∞

Substituindo:

1,0267 T 12 = T 11 + 0,8

Aqui nós podemos usar até o solver do Excel para nos ajudar:

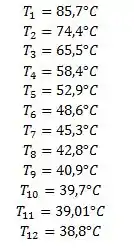
Beleza !! Achamos a distribuição de temperatura e agora nós vamos ver se a hipótese de transferência de calor unidimensional é razoável para essa aleta, ok?

A transferência de calor unidimensional é justificada quando o número de Biot é:

B i < 0,1

Se:

B i = h w 2 k = 500 W m 2 K 6 × 10 - 3   m 2 50 W m K = 0,03

Ou seja, neste caso:

B i < 0,1

E nossa hipótese é super válida !!

Passo 2

Na letra (b) nós temos que a taxa de transferência de calor na aleta, certo?

Analisando a figura nós vemos que existe um calor q 0 entrando, que é o calor que entra na aleta, também temos q 1 e a transferência de calor por convecção, q c o n v :

q 0 + q 1 + q c o n v = 0

Se substituirmos cada termo:

q 1 = k w T 1 - T 0 ∆ x

q c o n v = h ∆ x T ∞ - T 0

Substituindo na fórmula e achando q 0 :

q 0 = k w T 0 - T 1 ∆ x + h ∆ x T 0 - T ∞

q 0 = 50 W m K 6 × 10 - 3   m 100 ° C - 85,7 ° C 4 × 10 - 3   m + 500 W m 2 K 6 × 10 - 3   m 100 ° C - 30 ° C

q 0 = 1205 W m

Quando nós usamos a equação 3.81 nós vemos que o calor nestas aleta também pode ser calculado como:

q 0 = h P k A c 1 2 θ b tanh ⁡ m L

Sabendo que:

θ b = T b - T ∞ = 100 ° C - 30 ° C = 70 ° C

m = h P k A c = 2 l h k l w = 2 500 W m 2 K 50 W m K 6 × 10 - 3   m = 57,74   m - 1

h P k A c = 2 h l 2 k w = 2 0,048   m 2 500 W m 2 K 50 W m K 6 × 10 - 3   m = 0,6912 W 2 K 2

Na fórmula:

q 0 = 0,6912 W 2 K 2 1 2 70 ° C tanh ⁡ 57,74   m - 1 × 0,048   m = 1203 W K

Bem próximo, não foi?

Passo 3

Na letra (c) quando nós variamos o coeficiente de h   =   10 ,   100 ,   500   e   1000 W m 2 K , obtemos diferente valores de temperatura ao longo da aleta, certo?

Faremos da mesma forma que nos Passo 1:

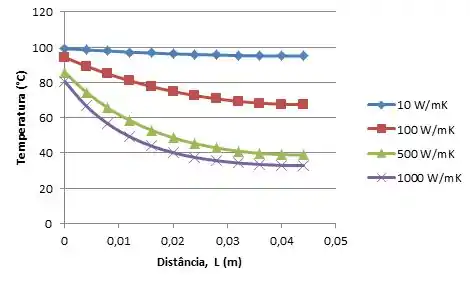
E para achar a taxa de transferência de calor na aleta em função de h é só fazermos novamente o Passo 2:

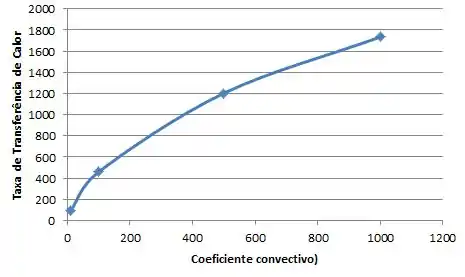
E finalizamos galerinha !!

Resposta

  2. q 0 = 1205 W m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A superfície superior de uma placa, incluindo os seus sulcos, é mantida a uma temperatura uniforme T 1=200 ° C . A superfície inferior se encontra a T 2=20 ° C . A condutividade térmica da placa é de
Uma fábula antiga descreve como um navio de madeira foi destruído por soldados que refletiram luz do sol nos seus escudos de bronze polido sobre o casco, fazendo o navio ficar em chamas. Para testar a
Seja o domínio bidimensional mostrado. Todas as superfícies estão isoladas a menos das superfícies isotérmicas em x = 0 e L. Use uma análise unidimensional para estimar o fator de forma S.Estime o fat
O fator de forma para a condução através do canto formado por duas paredes adjacentes, com D L 5 , sendo D e L a profundidade e a espessura da parede, respectivamente, é mostrado na Tabela 4.1. O elem
A diagonal de uma longa barra triangular se encontra isolada, enquanto as superfícies laterais, de comprimentos equivalentes, são mantidas a temperaturas uniformes Ta e Tb.Estabeleça uma rede nodal co