Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 104
O submarino russo da classe Tufão tem 170 m de comprimento e diâmetro máximo de 23 m. Seu propulsor pode fornecer até 80.000 hp à água do mar. Modele o submarino como um elipsoide 8:1 e calcule sua velocidade máxima, em nós.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos um submarino de comprimento e diâmetro máximo , com um propulsor que fornece uma potência de à água do mar.
O enunciado nos pede então pra calcular a velocidade máxima , em nós, pra manter essa potência. Pra isso, vamos considerar a relação da potência com a força de arrasto , dada pela equação abaixo:
Sendo: o coeficiente de arrasto para um elipsoide; a massa específica da água; e a área frontal do submarino como um elipsoide.
No próximo passo eu vou te mostrar como calcular a partir dessa equação, então vem comigo pra gente resolver esse problema juntos!
Passo 2
Pra resolver o problema, devemos calcular o coeficiente de arrasto .
O enunciado nos sugeriu que considerássemos o submarino como um elispoide de razão comprimento:diâmetro 8:1. Vamos então na Tabela 7.3 na página 495:
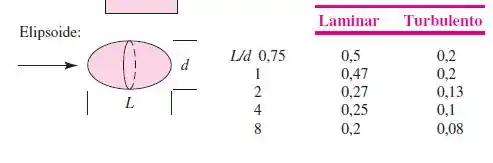
Como as dimensões do submarino são enormes, sabemos que o escoamento é com certeza turbulento e, portanto, podemos assumir a partir da figura acima.
Substituindo essa e as outras informações fornecidas no enunciado, teremos:
Pronto, matamos a questão juntos!
Resposta
A velocidade máxima necessária para manter a potência requerida é