Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 12

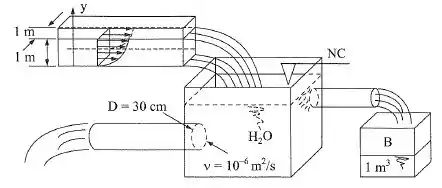
O tanque da figura abaixo permanece em nível constante. O escoamento na calha tem uma seção transversal quadrada e é bidimensional, obedecendo à equação v = 3 y 2 . Sabendo que o tanque B tem 1   m 3 e é totalmente preenchido em 5   s e g u n d o s e que o conduto circular tem 30   c m de diâmetro, determinar:

  1. A velocidade média na calha quadrada;
  2. A vazão no conduto circular de 30   c m de diâmetro;
  3. A velocidade máxima na seção do conduto circular de 30   c m de diâmetro.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Item “a”:

Para resolvermos o problema proposto, e determinarmos a velocidade média na calha quadrada, utilizaremos a seguinte equação:

v m = 1 A ∫ v d A

Com o perfil de velocidade fornecido na questão, substituiremos a integral e encontraremos a velocidade média:

v m = 1 1 ∫ 0 1 3 y 2 b d y

v m = 3 ∫ 0 1 y 2 d y

v m = 3 ( 1 ) 3 3 = 1   m / s

Passo 2

Item “b”:

Temos que:

Q B = V B ∆ t

Substituindo os valores, temos que:

Q B = 1 5

Q B = 0,2   m 3 / s

A vazão da calha é dada por:

Q c a l h a = v m A c a l h a

Logo:

Q c a l h a = 1 1

Q c a l h a = 1   m 3 / s

Pela equação da continuidade, temos que:

Q c a l h a = Q B + Q t u b o

Logo:

Q t u b o = 1 - 0,2

Q t u b o = 0,8   m 3 / s

Passo 3

Item “c”:

Com a vazão do tubo conhecida, podemos encontrar a sua velocidade média:

v m t u b o = Q t u b o A t u b o

v m t u b o = 0,8 π 0,3 2 4

v m t u b o = 11,32   m / s

Podemos calcular o número de Reynolds para descobrir se o escoamento é turbulento ou laminar. Temos que:

R e = v D v

R e = 11,32 0,3 10 - 6

R e = 3,4 ⋅ 10 6

O que indica um escoamento turbulento. Sabemos que para tal escoamento a velocidade média é dada por:

v m = 49 60 v m á x

Portanto:

v m á x = 60 49 11,32

v m á x = 13,86   m / s

Resposta

a )   v m = 1   m / s

b )   Q t u b o = 0,8   m 3 / s

c )   v m á x = 13,86   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está fazendo cerveja. O primeiro passo é encher o garrafão de vidro com o mosto líquido. O diâmetro interno do garrafão é 37,5c m , e você deseja enchêlo até o nível de 0,6m . Se o seu mosto é re
Água escoa em regime permanente através de um tubo de comprimento L e raio R=75m m . Calcule a velocidade de entrada uniforme, U , se a distribuição de velocidade através da saída é dada por u = u m á
Você está tentando bombear água para fora de seu porão durante uma tempestade. A bomba pode extrair 0,6L / s . O nível de água no porão está agora reduzindo a uma taxa de 0,4m m / m i n . Qual é a vaz
Em um escoamento a montante em regime permanente, a massa específica é 1k g / m 3 , a velocidade é 1000m / s , e a área é 0,1m 2 . A jusante, a velocidade é 1500m / s , e a área é 0,25m 2 . Qual é a m
Em sua cozinha, a pia tem 0,6m por 45,7c m e tem 30,5c m de profundidade. Você a está enchendo com água com uma vazão de 252 × 10 - 6m 3 / s . Quanto tempo (em minutos) você leva para encher metade da