Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 141
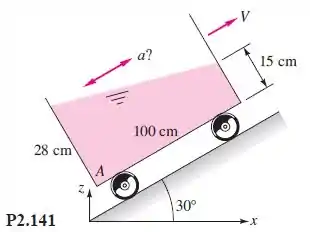
O mesmo tanque do Problema P2.139 agora está se movendo com aceleração constante subindo um plano inclinado de , como mostra a Figura P2.141. Considerando o movimento de corpo rígido, calcule (a) o valor da aceleração , (b) se a aceleração é para cima ou para baixo e (c) a pressão manométrica no ponto se o fluido for mercúrio a .
Passo 1
Fala galera!!
Nessa questão nós queremos (a) o valor da aceleração , (b) se a aceleração é para cima ou para baixo e (c) a pressão manométrica no ponto se o fluido for mercúrio para a configuração do tanque como mostrado na figura.
Passo 2
(a) Como a tangente de um angulo pode ser dado pelo cateto oposto divido pelo cateto adjacente, podemos dizer que a superfície está inclinada em relação ao tanque com um ângulo de:
Dessa forma, a superfície livre é inclinada no ângulo
Logo, este ângulo deve satisfazer a equação:
Mas a inclinação de restringe a aceleração de modo que , .
Portanto:
, . portanto
Os componentes cartesianos são e .
Passo 3
(b) Pelos cálculos feitos no item anterior, podemos perceber que a aceleração é para baixo.
Passo 4
(c) A distância normal da superfície até o ponto é . Portanto, temos que:
Resposta
(a)
(b) Aceleração para baixo
(c)