Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 6

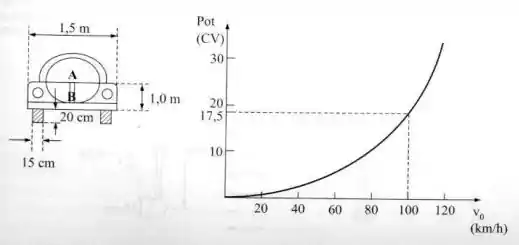
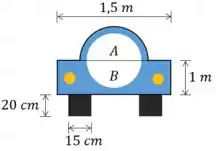
No teste de um veículo, num túnel aerodinâmico, foi levantada a curva de potência gasta para vencer a força de arrasto do ar em função de sua velocidade. Sendo a vista frontal do veículo indicada na figura, determinar o seu coeficiente de arrasto. Dados: ρ a r = 1,2   k g / m 3 ; Área A = 0,72   m 3 ; Área B considerada retangular.

Passo 1

Dados da questão:

  • ρ a r = 1,2   k g / m 3
  • A A = 0,72   m 2

A questão pede:

  • O coeficiente de arrasto: C a = ?

Passo 2

Vamos iniciar calculando a área frontal do carro:

A f r o n t a l = A A + A B + 2 A p n e u

A f r o n t a l = 0,72   m 2 + 1 m ⋅ 1,5 m + 2 ⋅ ( 20   c m ⋅ 15   c m )

A f r o n t a l = 0,72   m 2 + 1,5   m 2 + 0,06   m 2

A f r o n t a l = 2,28   m 2

Passo 3

Agora precisamos saber quanto de potência é consumida. Como o coeficiente de arrasto é constante, podemos escolher qualquer ponto do gráfico. Vamos pegar o ponto destacado pelas linhas pontilhadas

N = 17,5   c v = 12900   W

v = 100 k m h = 27,8 m s  

Passo 4

A potência consumida pelo arrasto pode ser dada por:

N = P a ⋅ v

Substituindo a fórmula do arrasto temos: N = C a ⋅ ρ a r ⋅ v 2 ⋅ A f r o n t a l 2 ⋅ v

Isolando o coeficiente de arrasto:

C a = 2 N ρ a r ⋅ v 3 ⋅ A f r o n t a l

Aplicando os valores:

C a = 2 ⋅ 12900   W 1,2   k g / m 3 ⋅ 27,8 m s 3 ⋅ 2,28   m 2

O resultado é:

C a = 0,44

Resposta

C a = 0,44

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma partícula esférica com raio a carregada negativamente, tendo uma carga, Q s , suspensa em um fluido dielétrico puro (não contendo íons). Quando submetido a um campo elétrico uniforme, E
Uma esfera de plástico oca com 0,5 cm de diâmetro contendo equipamento para teste de poluição está sendo dragada através do Rio Hudson em Nova York por um mergulhador que conduz um dispositivo subaquá
Considere a ciclista no Problema 9.9. Ela agora tem que subir uma colina com inclinação de 5%. Qual é a velocidade máxima que ela pode atingir? Qual é a velocidade máxima, se há também um vento contrá
Umcarroesportivode134,23kW,comáreafrontalde1,72m2,ecoeficientedearrastode0,31,requer12,677kWparatrafegara 100km/h.Paraqualvelocidadeoarrastoaerodinâmicosuperarápelaprimeiravezaresistênciaderolamento?(
Você é um engenheiro de projetos e foi encarregado de projetar um sistema de frenagem de emergência por paraquedas, para uso em um avião militar de massa igual a 9500 kg. O avião aterrissa a 350 km/h