Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 95

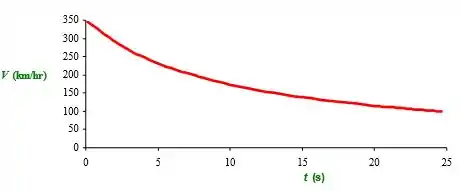
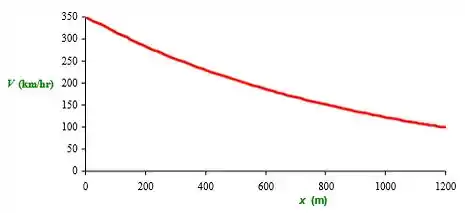
Você é um engenheiro de projetos e foi encarregado de projetar um sistema de frenagem de emergência por paraquedas, para uso em um avião militar de massa igual a 9500 kg. O avião aterrissa a 350 km/h e o sistema de paraquedas sozinho deve reduzir a velocidade do avião para 100 km/h em menos de 1200 m. Determine o diâmetro mínimo requerido para um único paraquedas e para três paraquedas não interferentes. Trace o gráfico da velocidade do avião em função da distância e também em função do tempo. Qual é a máxima “força g” sofrida?

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que, por definição:

F A = C A 1 2 ρ V ² A

Aplicando a segunda lei de Newton para a aeronave:

M d V d t = - C A 1 2 ρ A V i 2

Integrando os dois lados:

V t = V i 1 + C A ρ A 2 M V i t → e q   1

Integrando de novo em relação a variável t :

x t = 2 M C A ρ A ln ⁡ 1 + C A ρ A 2 M V i t → e q   2

Combinando as equações 1 e 2 e eliminando o t :

x = 2 M C A ρ A ln ⁡ V i V → e q   3

Para acharmos a área mínima do paraquedas, temos que isolar a área e substituir x = x f e V = V f :

A = 2 M 3 C A ρ x f ln ⁡ V i V f

A máxima força g é dada por:

d V d t g = - C A ρ A V 2 2 M g

Agora, com a ajuda do Excel, podemos determinar os valores pedidos para os casos de 1 e de 3 paraquedas:

A 1 = 11,4 m 2

D 1 = 3,8 m

A 3 = 3,8 m 2

D 3 = 2,2 m

g m á x = - 1,01

Passo 2

Agora, basta fazer os gráficos no Excel:

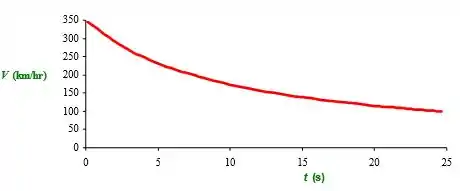
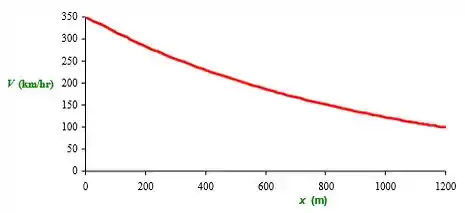
Resposta

A 1 = 11,4 m 2

D 1 = 3,8 m

A 3 = 3,8 m 2

D 3 = 2,2 m

g m á x = - 1,01

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The Army’s new ATPS personnel parachute is said to beable to bring a 400-lbf load, trooper plus pack, to ground at16 ft/s in “mile-high” Denver, Colorado. If we assume thatTable 7.3 is valid, what is
If a missile takes off vertically from sea level and leavesthe atmosphere, it has zero drag when it starts and zerodrag when it finishes. It follows that the drag must be amaximum somewhere in between
The ultralight plane Gossamer Condor in 1977 was the firstto complete the Kremer Prize fi gure-eight course under human power. Its wingspan was 29 m, with Cav 5 2.3 m and atotal mass of 95 kg. The dra
The Beechcraft T-34C aircraft has a gross weight of5500 lbf and a wing area of 60 ft2 and fl ies at 322 mi/h at10,000-ft standard altitude. It is driven by a propeller thatdelivers 300 hp to the air.
The world’s largest airplane, the Airbus A380, has a maximum weight of 1,200,000 lbf, wing area of 9100 ft2, wingspan of 262 ft, and CDo 5 0.026. When cruising atmaximum weight at 35,000 ft, the four