Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 58
Trace as linhas de corrente do escoamento combinado de um sumidouro na origem e fontes de intensidade em e . Dica: Irá aparecer um cilindro de raio .
Passo 1
E aí, tudo bem? Bora matar essa questão!
Essa é bem simples, só precisamos organizar nosso escoamento, da equação temos:
Considerando a dica que a questão nos deu, vamos fazer o desenho para essa questão:
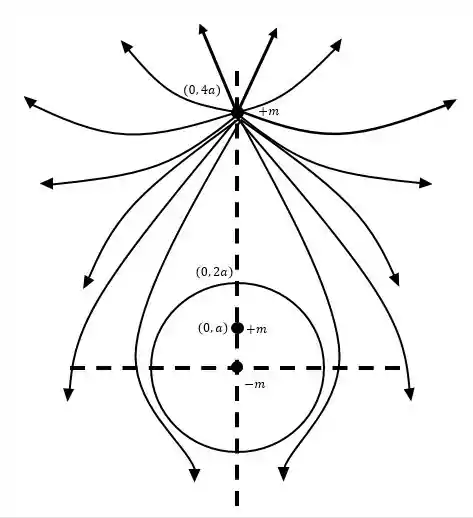
As questões e temos outros exemplos de questões com potenciais, temos elas aqui no site, se for necessário dá uma olhadinha lá!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Desenho vide passo a passo!
Exercícios de Livros Relacionados
Explique por que a aproximação de escoamento incompressível e a aproximação de temperatura constante usualmente caminham lado a lado.
Analise e discuta um caso limite do Problema 9 - 89 no qual não há cilindro interno ( R i = ω i = 0 ). Encontre uma expressão de u θ em função de r . Que tipo de escoamento é este? Descreva como esse
Considere novamente o tubo anular representado na Figura P 9 - 91 . Suponha que a pressão seja constante em todos os pontos (não há gradiente de pressão empurrando o escoamento). Porém, suponha que a
Repita o Problema 9 - 92 invertendo as paredes estacionária e móvel. Particularmente, faça a parede interna estacionária e a parede do tubo externo se movendo a uma velocidade constante V para a direi
Analise e discuta dois casos limites do Problema 9 - 87 .(a) O espaçamento é muito pequeno. Mostre que o perfil de velocidade se aproxima de uma função linear da parede do cilindro externo até a pared