Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 7
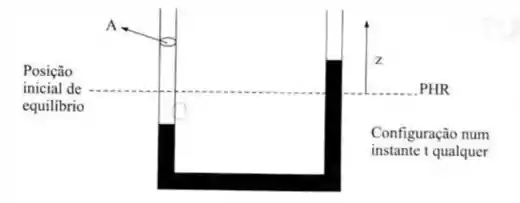
No tubo em U da figura, de seção de área A, oscila, em torna da posição de equilíbrio, uma coluna de comprimento total L de um líquido admitido ideal. Determinar o período T da oscilação.
Passo 1
Pela equação 10.18:
Considerando que não há perdas e nem fontes de externas de potência
Para um líquido incompressível ideal:
Pondo a gravidade para fora da integral:
Como a velocidade é normal à saída:
Integrando:
Organizando:
Passo 2
Observando o manômetro, percebemos que o ponto (1) e (2) são abertos para a atmosfera:
Por ser uma oscilação, a diferença entre as alturas e o ponto de referência é sempre igual, mas oposta:
Pela mesma lógica, as velocidades tem o mesmo módulo, então, quando elevadas ao quadrado:
Então:
Passo 3
Reorganizando
Para o volume de controle não há variação de energia potencial, pois quando um lado sobe, o outro desce. Então a expressão:
Logo:
Como a velocidade não varia com o volume:
Integrando:
Passo 4
A velocidade só é função do tempo dentro do percurso . Nesse momento o volume é dado por
Derivando:
A vazão é dada por:
Mas a velocidade é função de . Pela regra da cadeia:
E:
Aplicando:
Passo 5
Integrando:
Subtraindo as constantes:
Quando a altura for máxima, a velocidade é igual a zero:
Aplicando>
Então a equação da velocidade é:
Passo 6
Também sabemos que:
Então:
Aplicando:
Chegamos em:
Integrando os dois lados:
Utilizando uma tabela de integrais:
Unindo as constantes:
Quando o tempo for zero a coluna estará em equilíbrio com
Passo 7
Se quando o tempo é zero a coluna está em equilíbrio, quando a coluna alcançar a altura máxima terá se passado 1 quarto do período. Então
Aplicando: