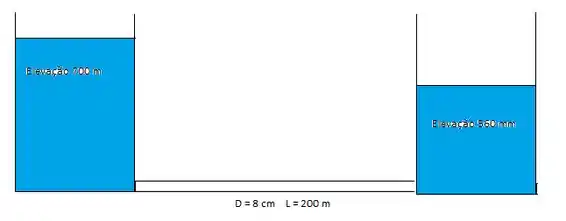
Um tubo liso de 8 cm de diâmetro liso e 200 m de comprimento conecta dois reservatórios contendo água a 20°C, em um deles a elevação da superfície livre é de 700 m e no outro é de 560 m. Se perdas localizadas são desprezadas, a vazão esperada através do tubo é:

2. 0,048 m³/h
3. 2,87 m³/h
4. 134 m³/h
5. 172 m³/h
6. 385 m³/h

Vamos agora aplicar nossa equação de energia para os dois pontos mostrados abaixo!

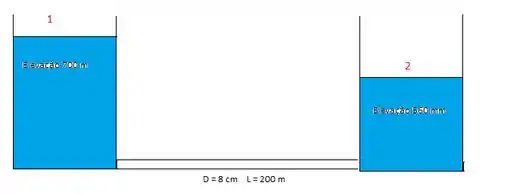
Note que temos os dois tanques abertos para atmosfera e, portanto, suas pressões também serão iguais nos pontos 1 e 2. As velocidades de superfície podem ser aproximadas a zero, com isso temos que:

Note que há entradas nos dois tanques rentes a eles, seus valores de . Mas note que isso faz parte da continha que teríamos que fazer para . Mas , ou seja, a sua contribuição é muito maior uma vez que ele estará multiplicado pelo comprimento do tubo que é 200 m. Então como

Note que precisamos de f, mas esse cara depende de Reynold que dependerá da velocidade. Então isso será um cálculo iterativo! Vamos chutar inicialmente

Opa, com esse novo valor de V, eu posso calcular Reynold!!

Mas pera, eu tive que chutar o valor de f, né? Então eu vou cair no cálculo iterativo, pois agora com esse novo valor de Re, eu vou na curva de tubo liso no diagrama de Moody e vou obter outro valor de f. Esse novo valor, substituir na equação de V, recalcular Reynold e fazer todo o processo novamente até convergência.

O Algoritmo é:

1. Chutar f
2. Calcular V
3. Calcular Re
4. Obter novo f para tubos lisos
5. Voltar ao passo (2) até convergência das velocidades.

Ao final do processo de convergência você obterá o valor de