Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 10

A two-dimensional, incompressible flow has the velocity

components u 5 4y and v 5 2x. (a) Find the acceleration

components. (b) Is the vector acceleration radial? (c) Sketch

a few streamlines in the first quadrant and determine if any

are straight lines.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

a) Calcule o componente de aceleração sobre o eixo x .

a x = u ∂ u ∂ x + v ∂ u ∂ y

Substitua 4 y por u , e 2 x por v .

a x     = ( 4 y ) ∂ ∂ x ( 4 y ) + ( 2 x ) ∂ ∂ y ( 4 y )       = ( 4 y ) × 0 + ( 2 x ) × 4       = 8 x  

Calcule o componente de aceleração sobre o eixo y .

a y = u ∂ v ∂ x + v ∂ v ∂ y

Substitua 4 y por u , e 2 x por v .

a y     = ( 4 y ) ∂ ∂ x ( 2 x ) + ( 2 x ) ∂ ∂ y ( 2 x )       = ( 4 y ) × 2 + ( 2 x ) × 0       = 8 y  

Assim, os componentes de aceleração são 8 x , 8 y .

Passo 2

b) Escreva a aceleração em forma vetorial.

a = a x i + a y j

Substitua 8 x por a x , e 8 y por a x .

a     = 8 x i + 8 y j       = 8 ( x i + y j )       = 8 r  

Assim, a aceleração vetorial é radial.

Passo 3

Escreva a equação para encontrar as simplificações.

d x u = d y v

Substitua 4 y por u , e 2 x por v .

  d x 4 y = d y 2 x     2 x d x = 4 y d y     x 2 = 2 y 2 +   c o n s t a n t e . . . ( 1 )    

Plote estes, para vários valores da constante C , no primeiro quadrante

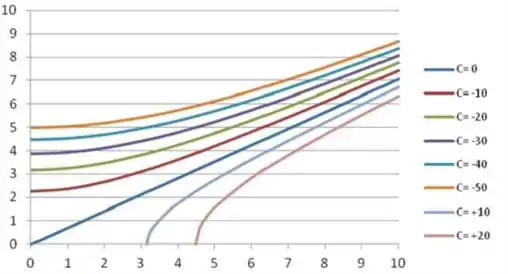
Passo 4

Ao considerar os gráficos, o fluxo acelera para a direita, com apenas uma linha reta

C = 0

Substitua 0 para C na equação (1)

  x 2 = 2 y 2 + 0     x = 2 y  

Assim, a função de linha reta é x = 2 y .

Resposta

a) a x = 8 x e a y = 8 y

b) A aceleração vetorial é radial

c) x = 2 y

Exercícios de Livros Relacionados

5.17 Deduza a forma diferencial da conservação da massa em coordenadas retangulares por expansão em série de taylor em torno do ponto O dos produtos da massa específica pelas componentes da velocidade
5.23 Avalie ∇ ⋅ ρ V → em coordenadas cilíndricas. Use a definição de ∇ em coordenadas cilíndricas. Substitua o vetor velocidade e aplique o operador gradiente, usando a informação da nota 1 de rodapé.
Um escoamento idealizado incompressível tem a distribuição tridimensional de velocidade proposta V = 4 x y 2 i + f y j - z y 2 k Encontre a forma apropriada da função f ( y ) que satisfaz a relação da
Suponha que o escoamento no bocal convergente da Figura P 4.2 tenha a forma V = V 0 [ 1 + ( 2 x ) / L] i . Calcule (a) a aceleração do fluido em x =L e (b) o tempo necessário para uma partícula de flu
Um campo de velocidade bidimensional é dado por u = - K y x 2 + y 2v = K x x 2 + y 2 em que K é constante. Esse campo satisfaz a continuidade incompressível? Transforme essas velocidades em componente