Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 22

Utilizando um volume de controle diferencial em x nas condições de escoamento em um tubo mostradas na Figura 8.8, deduza a Equação 8.45a.

Passo 1

E aí turminhaa!!

Animadíssimos para seguir?!

Vamos relembrar a Figura 8.8:

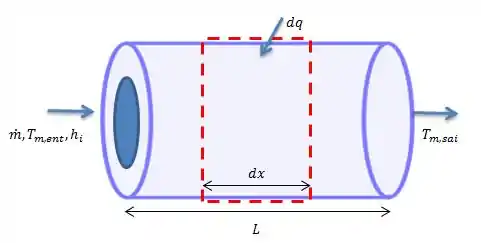
Como nós temos de calor convectivo entrando no tubo podemos usar a relação:

d q = m ˙ c p d T m

Ela também pode ser escrita em termos do coeficiente geral de transferência de calor:

d q = U . d A . T ∞ - T m

Podemos ainda reescrever a variação da área:

d A = P . d x

Portanto:

d q = U P . T ∞ - T m . d x

Relacionando as duas equações para d q :

m ˙ c p d T m = U P . T ∞ - T m . d x

d T m T ∞ - T m = U P m ˙ c p . d x

Passo 2

Vamos fazer uma adaptação aqui, ok? E vamos chamar:

d T m T ∞ - T m = - d ∆ T ∆ T

d ∆ T ∆ T = - P m ˙ c p . U d x

Bora integrar?

∫ ∆ T e n t ∆ T s a i d ∆ T ∆ T = - P m ˙ c p . ∫ 0 L U d x

Vamos fazer mail uma adaptação para facilitar achar o resultado que queremos!

Vamos multiplicar o denominador e o numerador por L:

ln ⁡ ∆ T s a i ∆ T e n t = - P L m ˙ c p . 1 L ∫ 0 L U d x

A expressão 1 L ∫ 0 L U d x nós conhecemos:

U - = 1 L ∫ 0 L U d x

Substituindo:

ln ⁡ ∆ T s a i ∆ T e n t = - P L m ˙ c p . U -

Para retirar o ln aplicamos o exponencial:

∆ T s a i ∆ T e n t = e - P L m ˙ c p . U -

Como assumimos:

∆ T s a i = T ∞ - T m ,   s a i

∆ T e n t = T ∞ - T m ,   e n t

Então:

T ∞ - T m ,   s a i T ∞ - T m ,   e n t = e - P L m ˙ c p . U -

E chegamos ao gran finale !!

Resposta

T ∞ - T m ,   s a i T ∞ - T m ,   e n t = e - P L m ˙ c p . U -

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja o escoamento laminar de um fluido com Pr = 4, com uma vazão, que passa por um processo de entrada combinada, com uma temperatura superficial constante, em um tubo com comprimento L
Água de resfriamento escoa através dos tubos, com paredes delgadas e diâmetro de 25,4m m , de um condensador de vapor de água a uma velocidade de 1m / s , enquanto uma temperatura superficial de 350K
O núcleo de um reator nuclear de alta temperatura, resfriado a gás, tem tubos de resfriamento com 20m m de diâmetro e 780m m de comprimento. Hélio entra no sistema a 600K e sai a 1000K , quando sua va
Considere o tubo revestido do Problema 4.29, mas agora leve em conta a presença de uma diferença entre a temperatura média do fluido, que muda ao longo do comprimento do tubo, e a temperatura do tubo.
N a K( 45 % / 55 % ) , que é uma liga de sódio e potássio, é usada para resfriar reatores nucleares de nêutrons rápidos. O N a K escoa a uma vazão de m ˙ =1k g / s através de um tubo com diâmetro D =