Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Circuito RC

Ver Todos os Exercícios

Teoria

Fala aí! Bora conversar sobre Circuito RC?

O que é um Circuito RC?

Um circuito RC é um circuito que é composto por uma fonte (força eletromotriz), resistor e capacitor. Ele tem essa carinha aqui:

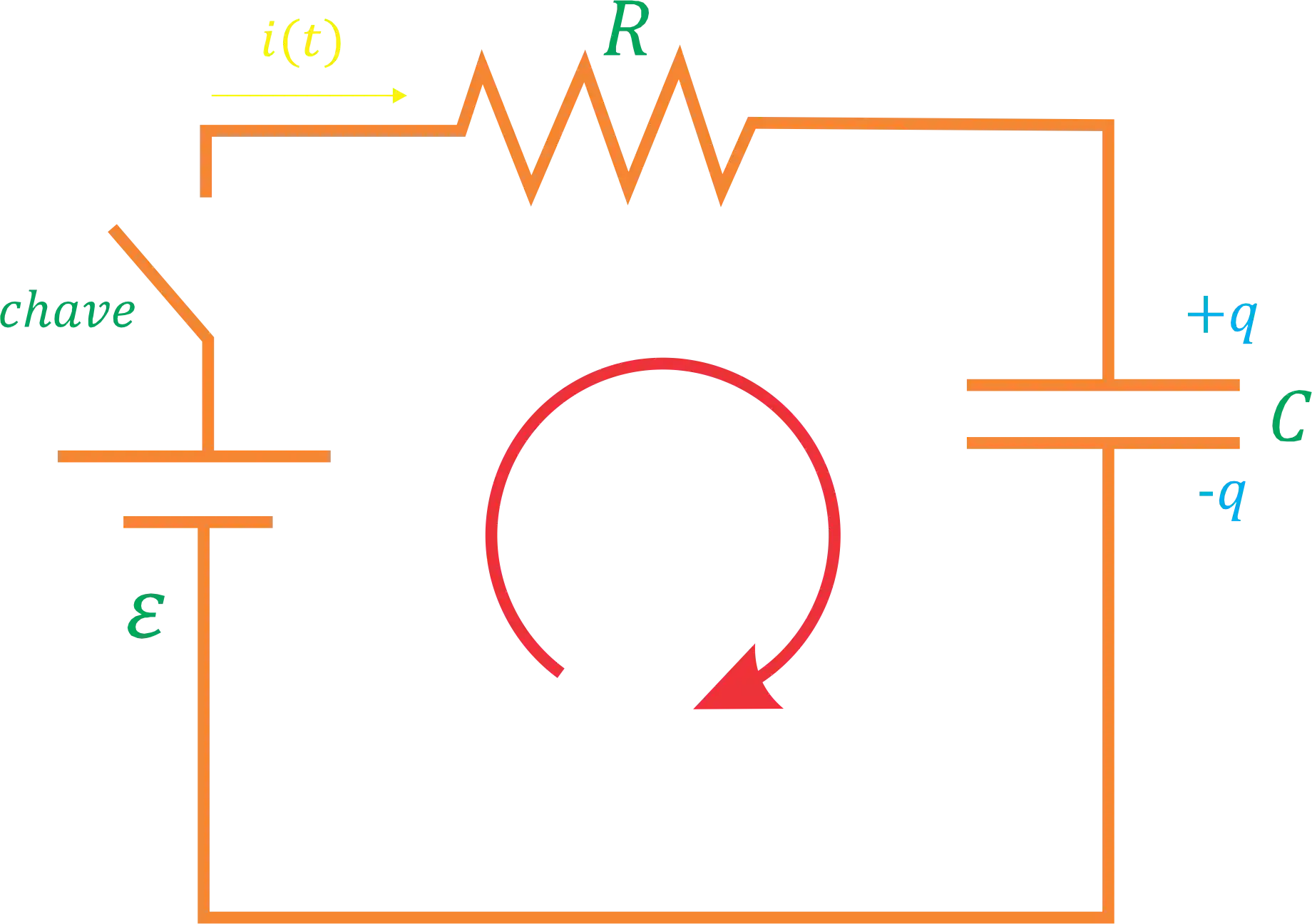
Representação de um circuito RC
Representação de um circuito RC

O capacitor é responsável pelo acúmulo de cargas para liberá-la no momento certo! Aqui a gente vai falar bastante sobre capacitor e capacitância, então se você ainda não tiver crack nesse assunto, dá uma conferida nessa página e depois volta correndo pra cá! Ok? 🏃🏃🏃

📢 Clique para ver mais:

Circuito RC: Fórmulas

Eu já vou te falar aqui duas fórmulas que são essenciais em um circuito RC! A primeira é a diferença de potencial do capacitor, quando ele está sendo carregado, é dada por:

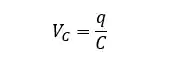
ddp do capacitor
ddp do capacitor

Onde:

  • é a diferença de potencial no capacitor;
  • é a carga do capacitor;
  • é a capacitância.

A corrente que passa no capacitor é dada por:

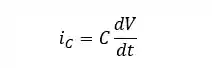
Corrente elétrica no capacitor
Corrente elétrica no capacitor

Onde:

  • é a corrente elétrica no capacitor;
  • é a capacitância;
  • é a taxa de variação da tensão do circuito com o tempo

Em um circuito RC, nós teremos alguns momentos em que o capacitor estará sendo carregado, ou seja, haverá carga sendo armazenada nele, e teremos outros momentos em que o capacitor estará sendo descarregado, ou seja, a carga que foi armazenada nele anteriormente estará sendo usada.

Vamos analisar cada uma dessas duas situações separadamente! Mas antes, que tal dar uma conferida nesse vídeo super completo sobre Circuito RC que o Responde Aí preparou pra você!

Carregamento do Capacitor

Vamos imaginar que no momento o capacitor começa a ser carregado. Podemos aplicar a Lei das malhas no circuito RC e teremos a seguinte expressão:

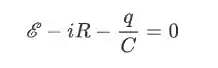
Lei das malhas aplicada a um circuito RC em carregamento
Lei das malhas aplicada a um circuito RC em carregamento

Se aplicarmos a definição de corrente, , a essa lei das malhas ficaremos com a seguinte expressão:

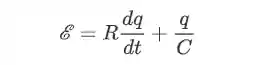
Definição de corrente aplicada a lei das malhas para um circuito RC
Definição de corrente aplicada a lei das malhas para um circuito RC

Essa é uma equação diferencial e sua solução é a que segue:

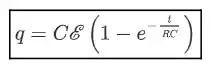
Solução da equação diferencial - expressão da carga em função do tempo
Solução da equação diferencial - expressão da carga em função do tempo

Assim, temos a expressão matemática que descreve como a carga no capacitor varia com o tempo.

Note que podemos tirar algumas conclusões disso, como:

  • Quando ; , que é exatamente o momento que o capacitor está começando a ser carregado, então nesse instante ainda não há carga armazenada nele;
  • Quando ; , que é a carga máxima do capacitor

Agora, podemos derivar em relação ao tempo a expressão que encontramos para a carga e acharmos a expressão da corrente no capacitor com o tempo:

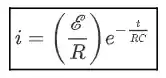
Expressão da corrente elétrica em função do tempo
Expressão da corrente elétrica em função do tempo

Podemos fazer um gráfico da corrente versus tempo e teremos esse perfil:

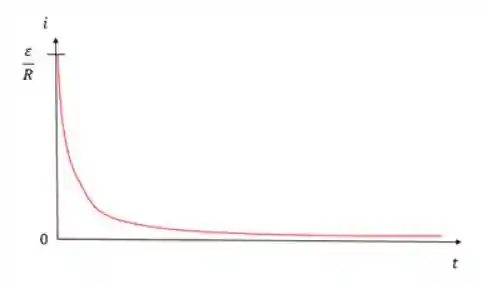
Gráfico da corrente
Gráfico da corrente

Note que a corrente começa com um valor máximo e conforme o capacitor vai sendo carregado a corrente vai diminuindo até começar a tender para zero.

Agora, podemos encontrar a expressão para a diferença de potencial em um capacitor, simplesmente pegando a expressão que achamos para a carga do capacitor e dividindo pela capacitância:

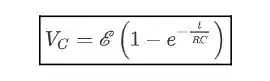
Expressão da diferença de potencial em função do tempo para um capacitor em carregamento
Expressão da diferença de potencial em função do tempo para um capacitor em carregamento

Podemos novamente fazer um gráfico da diferença de potencial versus tempo e encontrar o seguinte perfil:

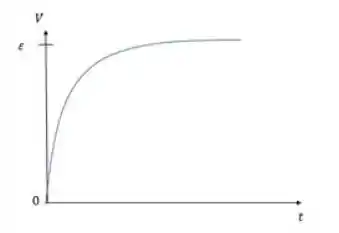
Gráfico da diferença de potencial
Gráfico da diferença de potencial

A diferença de potencial começa em zero e vai aumentando conforme o capacitor vai sendo carregado.

Descarga do Capacitor

A descarga do capacitor se dá em um circuito que a fonte (força eletromotriz) foi retirada e então o capacitor passa a agir como a fonte do circuito. Ou seja, em uma descarga do capacitor nós temos um circuito formado apenas pelo capacitor e pelo resistor.

Se aplicarmos a lei das malhas para esse circuito teremos a seguinte expressão:

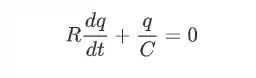
Lei das malhas aplicada à descarga do capacitor
Lei das malhas aplicada à descarga do capacitor

Novamente estamos diante de uma equação diferencial que tem a seguinte solução:

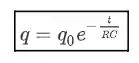
Solução da equação diferencial
Solução da equação diferencial

E assim, encontramos a expressão da carga em função do tempo na descarga de um capacitor. Analisando a fórmula vemos que quanto tende a a carga é , que é a carga máxima do capacitor, e conforme vai aumentando a carga vai diminuindo até tender a quando tende ao infinito. Novamente podemos derivar essa expressão em relação ao tempo e encontrar a expressão para a corrente elétrica:

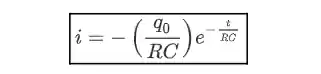
Expressão da corrente elétrica em função do tempo na descarga de um capacitor
Expressão da corrente elétrica em função do tempo na descarga de um capacitor

Fazendo um gráfico temos:

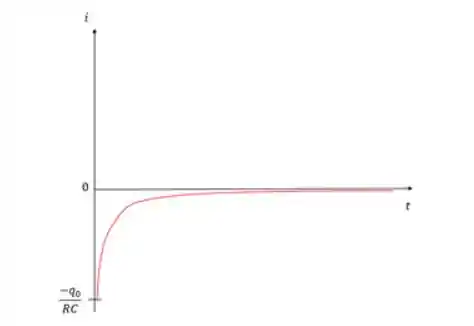
Gráfico da corrente elétrica
Gráfico da corrente elétrica

Note que na descarga o comportamento da corrente é o inverso do que no carregamento, aqui ela começa em um valor mínimo e vai aumentando com o tempo até tender a quando tendo ao infinito. Novamente podemos pegar a expressão da carga e dividir pela capacitância para encontrar a expressão da diferença de potencial:

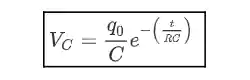
Expressão da diferença de potencial para a descarga de um capacitor
Expressão da diferença de potencial para a descarga de um capacitor

E o gráfico fica com esse perfil:

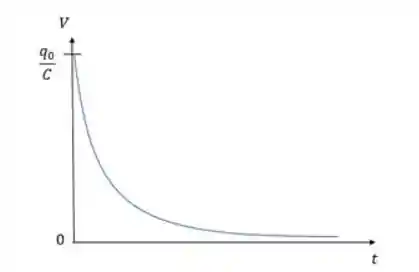
Gráfico da diferença de potencial
Gráfico da diferença de potencial

Circuito RC em Série ou em Paralelo

A última coisa que temos para falar em um circuito RC é a associação de capacitores em série ou em paralelo.

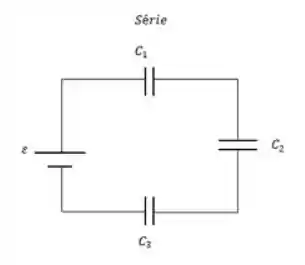
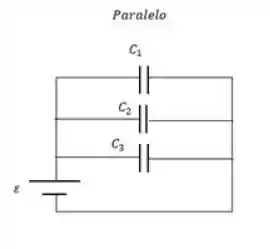
Capacitores em série
Capacitores em série

Capacitores em série
Capacitores em série

Nessas associações nós vamos ter que achar a capacitância equivalente para podermos fazer os cálculos. Para capacitores em série a capacitância equivalente é dada por:

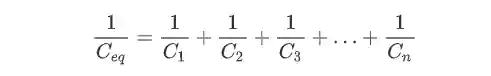
Capacitância equivalente para associação de capacitores em série
Capacitância equivalente para associação de capacitores em série

E para capacitores em paralelo a capacitância equivalente é dada por:

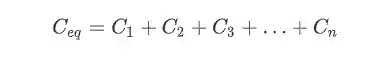
Capacitância equivalente para capacitores em paralelo
Capacitância equivalente para capacitores em paralelo

UFAAAAA!! Acabamos! Agora vamos praticar com exercícios?

Carregamento do Capacitor

Descarga do Capacitor

Circuito RC em Série ou em Paralelo

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2006, pp 189-11.

O interruptor está na posição da figura por um longo tempo. No instante t =   0 ele é trocado para a posição b . Determine a carga do capacitor e a corrente no resistor nos tempos:

a ) No instante em que a chave é fechada.

b ) t = 50 μ s

c )   t = 200 μ s

Passo 1

a )

Para determinar a carga no capacitor quando a chave é fechada, precisamos lembrar da seguinte relação:

Q = V . C

Onde V é a diferença de potencial e C é a capacitância, substituindo, temos:

Q = 9 .   4 × 10 - 6

Q = 3,6 × 10 - 5   C

A corrente no resistor é dada por:

V = 9 = R i = 25 . i

i = 0,36   A

Passo 2

Para determinar a carga no capacitor em diferentes tempos, precisamos lembrar da equação para a carga de um capacitor descarregando:

Q ( t ) = Q 0 . e - t τ

Onde Q 0 é a carga inicial e τ = R . C e é a denominada constante de tempo capacitiva, como já temos a carga inicial, vamos então calcular τ :

τ = R . C = 25 .   4 × 10 - 6 = 10 - 4   s

Substituindo na equação, temos:

Q t = 3,6 × 10 - 5 . e - t 10 - 4

Já a corrente no descarregamento de um capacitor é dada por:

i t = - Q 0 τ e - t τ = - 3,6 × 10 - 5 10 - 4 e - t 10 - 4

O sinal negativo da corrente na fórmula só indica que o seu sentido é contrário àquele do carregamento.

Passo 3

b )

Para t = 50 μ s , temos:

Q t = 3,6 × 10 - 5 . e - t 10 - 4

Q 50 μ s = 3,6 × 10 - 5 . e - 5 0 × 10 - 6 10 - 4

Q 50 μ s = 2,18 × 10 - 5   C

i 50 μ s = - 3,6 × 10 - 5 10 - 4 e - 50 × 10 - 6 10 - 4 = - 0,22   A

Em módulo:   i 50 μ s = 0,22   A

Passo 4

c )

Para t = 200 μ s , temos:

Q t = 3,6 × 10 - 5 . e - t 10 - 4

Q 200 μ s = 3,6 × 10 - 5 . e - 200 × 10 - 6 10 - 4

Q 200 μ s = 4,87 × 10 - 6   C

i 20 0 μ s = - 3,6 × 10 - 5 10 - 4 e - 200 × 10 - 6 10 - 4 = - 0,049   A

Em módulo:   i 20 0 μ s = 0,049   A

Resposta

a ) Q = 3,6 × 10 - 5   C ; i = 0,36   A  

b ) Q 50 μ s = 2,18 × 10 - 5   C ;   i 50 μ s = 0,22   A

c ) Q 200 μ s = 4,87 × 10 - 6   C ;   i 200 μ s = 0,049   A

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 193-47.

Um resistor de 15,0   k Ω e um capacitor estão ligados em série, e então uma diferença de potencial de 12,0   V é repentinamente aplicada entre as extremidades deles.

A diferença de potencial entre as extremidades do capacitor aumenta para 5,0   V em 1,30   μs .

  1. Calcule a constante de tempo do circuito;
  2. Determine a capacitância do capacitor;

Passo 1

O circuito tem mais ou menos essa cara aqui:

Trata-se de um circuito RC, nele a carga do capacitor, a corrente e d.d.p. do capacitor variam de acordo com as equações:

q = C ξ ( 1 - e - t / R C )

i = ξ R   e - t / R C

V C = ξ ( 1 - e - t / R C )

O circuito RC possui uma grandeza chamada constante de tempo, dada por:

τ = R C

Passo 2

  1. Calcule a constante de tempo do circuito;

    2. O problema diz que a diferença de potencial entre as extremidades do capacitor aumenta para 5,0   V em 1,30   μ s .

    Então vamos usar esse dado na equação:

    V C = ξ ( 1 - e - t / τ )

    Onde:

    V C = 5   V ;

    ξ = 12   V ;

    t = 1,30   μs ;

    Vamos ver no que vai dar:

    5 = 12 ( 1 - e - 1,3 / τ )

    5 12 = 1 - e - 1,3 / τ

    e - 1,3 τ = 1 - 5 12

    e - 1,3 τ = 7 12

    - 1,3 τ = ln ⁡ 7 12

    - 1,3 τ = - 0,53

    τ = 1,3 0,53

    τ = 2,4   μs

    Passo 3

  2. Determine a capacitância do capacitor;

Conforme eu disse no Passo 1:

τ = R C

Logo:

C = τ R

Agora ficou fácil, né?

τ = 2,4   μs = 2,4 × 10 - 6   s ;

R = 15   k Ω = 1,5 × 10 4   Ω ;

Vambora!

C = 2,4 × 10 - 6 1,5 × 10 4

C = 160   p F

Resposta

  1. τ = 2,4   μs ;
  2. C = 160   p F ;

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2006, pp 195-65.

No circuito abaixo, ε = 1,2   kV , C = 6,5   μF , R 1 = R 2 = R 3 = 0,73   M Ω .

Com o capacitor C completamente descarregado, a chave S é fechada bruscamente no instante t = 0 .

Determine, para o instante t = 0 :

  1. A corrente i 1 no resistor 1;
  2. A corrente i 2 no resistor 2;
  3. A corrente i 3 no resistor 3;

    4. Determine, para t → ∞ (ou seja, após várias constantes de tempo):

  4. i 1 ;
  5. i 2 ;
  6. i 3 ;

    7. Determine a diferença de potencial V 2 no resistor 2:

  7. Em t = 0 ;
  8. Em t → ∞   ;
  9. Faça um esboço do gráfico de V 2 em função do tempo t no intervalo entre esses dois instantes extremos;

Passo 1

  1. Determine, para o instante t = 0 a corrente i 1 no resistor 1;

    2. O que a gente tem que atentar aqui é que a voltagem em um capacitor é dada pela seguinte expressão:

    V = q C

    Em t = 0 o capacitor está descarregado, ou seja, q = 0 e pela fórmula, a diferença de potencial no capacitor também será nula. Assim, nesse momento é como se o capacitor não existisse:

    Passo 2

    Agora, nós temos a seguinte situação no circuito:

    Note que podemos dividir o circuito em duas malhas:

  • Malha 1: Resistores R 1 e R 2
  • Malha 2: Resistores R 1 e R 3

Vamos aplicar a Lei das Malhas para cada uma das malhas:

Malha 1:

ε - i 1 R 1 - i 2 R 2 = 0

Malha 2:

ε - i 1 R 1 - i 3 R 3 = 0

Temos duas equações, mas três variáveis ( i 1 , i 2 e i 3 ), então para resolver precisamos de mais uma equaçãozinha.

Vamos utilizar a Regra dos Nós, que nos diz que:

i 1 = i 2 + i 3

Então:

i 3 = i 1 - i 2

Se substituirmos a expressão para i 3 na Lei das malhas para a Malha 2 teremos um sisteminha de duas equações:

ε - i 1 R 1 - i 2 R 2 = 0

ε - i 1 R 1 - i 1 - i 2 R 3 = 0

Passo 2

Bora resolver esse sisteminha!!

ε - i 1 R 1 - i 2 R 2 = 0

ε - i 1 R 1 - i 1 - i 2 R 3 = 0

Onde:

ε = 1,2   kV = 1,2 × 10 3   V ;

R 1 = R 2 = R 3 = 0,73   M Ω = 7,3 × 10 5   Ω ;

Logo:

1,2 × 10 3 - 7,3 × 10 5   i 1 - 7,3 × 10 5   i 2 = 0

1,2 × 10 3 - 14,6 × 10 5   i 1 + 7,3 × 10 5   i 2 = 0  

Somando as duas equações:

2,4 × 10 3 - 21,9 × 10 5   i 1 = 0

i 1 = 2,4 × 10 3 21,9 × 10 5

i 1 = 1,1 × 10 - 3  A = 1,1  mA

Passo 3

  • Determine, para o instante t = 0 a corrente i 2 no resistor 2;

    • Para descobrir o valor de i 2 é só utilizar uma das equações do nosso sisteminha:

    Vamos usar essa

    ε - i 1 R 1 - i 2 R 2 = 0

    Onde:

    i 1 = 1,1   × 10 - 3   A ;

    Que encontramos anteriormente

    A nossa única incógnita é i 2 :

    1,2 × 10 3 - 7,3 × 10 5   .     1,1 × 10 - 3 - 7,3 × 10 5   i 2 = 0

    Logo:

    i 2 = 5,5   × 10 - 4  A = 0,55  mA  

    Passo 4

  • Determine, para o instante t = 0 a corrente i 3 no resistor 3;

    • Como já temos o valor de i 1 e i 2 , para achar i 3 vamos retornar para a Regra dos Nós:

    i 3 = i 1 - i 2

    Onde:

    i 1 = 1,1   m A ;

    i 2 = 0,55   m A ;

    Logo:

    i 3 = 0,5 5   m A

    Passo 5

  • Determine, para o instante t → ∞ a corrente i 1 no resistor 1;

    • Quando t → ∞ , o capacitor fica completamente carregado, portanto, a corrente deixa de correr no ramo onde ele está.

    Ou seja, i 3 = 0  

    Além disso, a corrente i 1 não se divide, pois só há um caminho para percorrer, então:

    i 1 = i 2

    Passo 6

    Vamos aplicar a Lei das malhas para essa nossa situação:

    ε - i 1 R 1 - i 2 R 2 = 0

    Como i 1 = i 2 e R 1 = R 2 , temos:

    ε - i 1 R 1 - i 1 R 1 = 0

    ε - 2   i 1 R 1 = 0

    ε = 2   i 1 R 1

    Então, i 1 será dada por:

    i 1 = ε 2 R 1 = 1,2.10 3 2 . 0,73.10 6 = 8,2   × 10 - 4   A = 0,82   m A

    Passo 7

  • Determine, para o instante t → ∞ a corrente i 2 no resistor 2;

    • Já vimos que i 1 = i 2 , então:

    i 2 = i 1 = 0,82   m A

    Passo 8

  • Determine, para o instante t → ∞ a corrente i 3 no resistor 3;

    • Já analisamos que nesse caso, nenhuma corrente passa pelo ramo do capacitor, então:

    i 3 = 0   A

    Passo 9

  • Determine a diferença de potencial V 2 no resistor 2 em t = 0 ;

    • Quando t = 0 a corrente que passa pelo resistor 2 é i 2 = 0,55   m A = 0,55 × 10 - 3 A . Logo:

    V 2 = R 2 i 2

    Onde R 2 = 0,73   M Ω = 0,73 × 10 6   Ω . Logo:

    V 2 = 0,73 × 10 6 × 0,55 × 10 - 3

    V 2 = 4,015 × 10 2   V = 401,5   V

    Passo 10

  • Determine a diferença de potencial V 2 no resistor 2 em t → ∞ ;

    • Quando t → ∞ , a corrente que passa pelo resistor 2 é i 2 = 0,82   m A = 0,82 × 10 - 3 A . Logo:

    V 2 = R 2 i 2

    V 2 = 0,73 × 10 6 × 0,82 × 10 - 3

    V 2 = 5,986   × 10 2 =   598,6   V

    Passo 11

  • Faça um esboço do gráfico de V 2 em função do tempo t no intervalo entre esses dois instantes extremos;

    • Vamos considerar agora a Malha 1 (que já identificamos no passo 2) e vamos definir uma Malha 3, formada pelo capacitor e pelos resistores 2 e 3.

    As equações das malhas serão:

    Malha 1:

    ε - i 1 R 1 - i 2 R 2 = 0

    Malha 3:

    - q C - i 3 R 3 + i 2 R 2 = 0

    Considerando que i 1 = i 2 + i 3 e que R 1 = R 2 = R 3 = R e substituindo isso na equação da Malha 1, teremos:

    ε - ( i 2 + i 3 ) R - i 2 R = ε - 2 i 2 R - i 3 R = 0

    i 2 = ( ε - i 3 R ) / 2 R

    Substituindo esse resultado na equação da Malha 3, temos:

    - q C - i 3 R + ε - i 3 R 2 R × R = 0

    - q C - i 3 R + ε 2 - i 3 R 2 = 0

    Sendo:

    i 3 = d q d t

    Temos:

    - q C - R d q d t + ε 2 - d q d t R 2 = 0

    3 R 2 d q d t + q C = ε 2

    Essa equação é semelhante àquela que vimos na teoria, com algumas pequenas diferenças. No nosso caso,

    τ = 3 R C 2

    E o potencial é:

      ε 2

    Logo, a solução dessa equação é:

    i 3 t = ε 3 R e - 2 t 3 R C

    Como vimos, a corrente i 2 será dada por:

    i 2 = ε - i 3 R 2 R

    Substituindo em i 2 a expressão que achamos para i 3 , temos:

    i 2 = ε - ε 3 R e - 2 t 3 R C R 2 R = ε 2 R - ε 6 R e - 2 t 3 R C

    Daí, temos:

    V 2 t = i 2 R = ε 2 R - ε 6 R e - 2 t 3 R C R =   ε 6 3 - e - 2 t 3 R C

    Então o gráfico da diferença de potencial tem mais ou menos essa cara:

    Resposta

    1. i 1 = 1,1   mA ;
    2. i 2 = 0,55   m A ;
    3. i 3 = 0,55   m A ;
    4. i 1 = 0,82   m A ;
    5. i 2 = 0,82   m A ;
    6. i 3 = 0   A ;
    7. V 2 = 401,5   V ;
    8. V 2 = 598,6   V ;

    Exercício Resolvido #4

    UNICAMP-P2-2012.2-Física III-Diurno-Questão n°3

    O circuito da figura contém dois resistores R 1 e R 2 e dois capacitores C 1 e C 2 e o conjunto é ligado a uma bateria de f e m ε . Antes de a chave S ser ligada, os capacitores estão descarregados.

    a ) determine a constante de tempo desse circuito;

    b ) determine a corrente que atravessa a bateria em função do tempo após o fechamento da chave S ;

    c ) determine a d d p entre os ponto b e c em função do tempo;

    d ) com S fechada por um longo tempo, quais são as cargas nos capacitores C 1 e C 2 .

    Passo 1

    a ) determine a constante de tempo desse circuito;

    Antes de começar o problema aqui, a primeira coisa que devemos fazer é simplificar esse circuito.

    Temos duas resistências em paralelo, de modo que a resistência equivalente será:

    1 R e q = 1 R 1 + 1 R 2

    R e q = R 1 R 2 R 1 + R 2

    Da mesma forma, temos dois capacitores em paralelo, de forma que a capacitância equivalente será:

    C e q = C 1 + C 2

    Assim, o circuito, que antes tinha uma cara escrota, agora ainda tem uma cara ainda escrota, mas um pouco melhor...

    Passo 2

    Isso agora nada mais é do que um circuito R C em série.

    Quando o capacitor está inicialmente descarregado, a equação que determina o seu carregamento, é dada por:

    q t = C ε 1 - e - t R C

    Onde o produto R C é chamado de constante de tempo capacitiva.

    Logo:

    τ C = R e q C e q

    τ C = R 1 R 2 R 1 + R 2   C 1 + C 2

    τ C = R 1 R 2 C 1 + C 2 R 1 + R 2

    Passo 3

    b ) determine a corrente que atravessa a bateria em função do tempo após o fechamento da chave S ;

    No passo anterior falamos um pouco de como a carga varia em função do tempo durante o carregamento, certo?

    Então, se queremos descobrir a corrente, a única coisa que temos que fazer aqui é derivar a expressão:

    q t = C ε 1 - e - t R C

    Logo:

    i t = d q t d t

    i t = ε R e q e - t R e q C e q

    Substituindo aqui a expressões de R e q e C e q :

    i t = ε R 1 + R 2 R 1 R 2   e - R 1 + R 2 R 1 R 2 C 1 + C 2   t

    Passo 4

    c ) determine a d d p entre os ponto b e c em função do tempo;

    Como as resistências R 1 e R 2 estão em paralelo:

    V b c = V 1 = V 2

    R 1 i 1 = R 2 i 2

    i 1 = R 2 R 1   i 2

    Entretanto, a soma das duas correntes deve ser sempre igual a i t , logo:

    i 1 + i 2 = i t

    R 2 R 1   i 2 + i 2 = i t

    i 2 R 1 + R 2 R 1 = i t

    i 2 = i t R 1 R 1 + R 2

    Agora ficou mais tranquilo pro nosso lado:

    V b c = V 2 = R 2 i 2

    V b c = i t R 1 R 2 R 1 + R 2  

    Substituindo a expressão de i t :

    i t = ε R 1 + R 2 R 1 R 2   e - R 1 + R 2 R 1 R 2 C 1 + C 2   t

    V b c = R 1 R 2 R 1 + R 2   ε R 1 + R 2 R 1 R 2   e - R 1 + R 2 R 1 R 2 C 1 + C 2   t

    V b c = ε   e - R 1 + R 2 R 1 R 2 C 1 + C 2   t

    Passo 5

    d ) com S fechada por um longo tempo, quais são as cargas nos capacitores C 1 e C 2 .

    Quando t → ∞ , o capacitor atinge a sua carga máxima e a corrente para de circular por ele.

    Como vimos antes, a carga do capacitor varia em função do tempo de acordo com a função:

    q t = C e q ε 1 - e - t R e q C e q

    Quando o capacitor atinge a sua carga máxima, diferença de potencial entre os seus terminais é igual a ε .

    Logo, depois de um tempo muito longo, os dois capacitores C 1 e C 2 estarão completamente carregados e a diferença de potencial entre os terminais de cada um deve ser igual a ε .

    ε = Q 1 C 1 → Q 1 = C 1 ε

    ε = Q 2 C 2 → Q 2 = C 2 ε

    Resposta

    a )

    τ C = R 1 R 2 C 1 + C 2 R 1 + R 2

    b )

    i t = ε R 1 + R 2 R 1 R 2   e - R 1 + R 2 R 1 R 2 C 1 + C 2   t

    c )

    V b c = ε   e - R 1 + R 2 R 1 R 2 C 1 + C 2   t

    d )

    Q 1 = C 1 ε

    Q 2 = C 2 ε

    Exercício Resolvido #5

    Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 26.72 adaptaddo, pp. 198

    O circuito indicado na figura abaixo mostra um capacitor que está inicialmente descarregado. A chave está fechada no instante t = 0 . Sobre essa situação,

    1. Qual é a corrente que passa através de cada resistor imediatamente após a chave ser fechada?
    2. Qual é a corrente que passa através de cada resistor imediatamente no instante de tempo t = ∞ ?
    3. Qual é a carga final do sobre o capacitor?

    Passo 1

    a) Qual é a corrente que passa através de cada resistor imediatamente após a chave ser fechada?

    Mostramos na teoria para você que se o capacitor está descarregado em t = 0 , então ele não tem carga nenhuma

    q t = 0 = 0

    Bom, se não tem carga alguma no capacitor, isso significa que a diferença de potencial V c t = 0 = V e f entre as placas também é zero, porque:

    V c = q C         →             V c t = 0 = V e f = q t = 0 C = 0

    No entanto, porém, todavia, como a corrente é diferente de zero através do capacitor, i t = 0 ≠ 0 , passa uma corrente também através do resistor R d e = 3,0   Ω , que está em série com o capacitor. Para t = 0 , então, como V c = V e f = 0 , podemos simplicar o circuito da figura acima para o seguinte:

    Passo 2

    Analisando esse novo circuito que redesenhamos, podemos ver que há uma associação de resistores, sendo que R b c e R d e estão em paralelo e o resultado dessa associação está em série com o resistor R a b .

    Primeiro vamos calcular a resistência equivalente, R e q 1 , para associação em paralelo de R b c e R d e :

    1 R e q 1 = 1 R b c + 1 R d e

    R e q 1 =   R b c R d e R b c + R d e

    Agora, vamos calcular a nossa resistência equivalente total, R e q , da associação em paralelo de R a b e R e q 1 :

    R e q = R a b + R e q 1

    Então a resistência equivalente nesse caso será:

    R e q = R a b + R b c R d e R b c + R d e

    Onde:

    R a b =   8   Ω

    R b c =   6   Ω

    R d e =   3   Ω

    Então:

    R e q = 3 × 6 3 + 6 + 8 = 10   Ω

    A corrente i t do circuito é dada por:

    i t = ε R e q  

    Então, a corrente i t = 0 é, então:

    i t = 0 = ε R e q = 42 10 = 4,2   A

    Passo 3

    b) Qual é a corrente que passa através de cada resistor imediatamente no instante de tempo t = ∞ ?

    Para o tempo t = ∞ fica ainda mais simples o circuito!! Duvida?? Então segue...

    Para um tempo muito grande, ou seja, t → ∞ , o capacitor fica totalmente carregado e nenhuma corrente flui mais através dele: i c t → ∞ = 0 . Então, também não passa nenhuma corrente pelo resistor R d e que está em série com esse capacitor! Isso significa que podemos “jogar fora” (=”analisar o circuito como se o componente não existissem”) esse resistor e o capacitor na nossa análise e simplificar o circuito para:

    Agoa só temos uma associação em série dos resistores R a b e R b c . Então a resistência equivalente será:

    R e q = R a b + R b c

    Como:

    R a b =   8   Ω

    R b c =   6   Ω

    Então:

    R e q = 14   Ω  

    Logo, a corrente será:

    i t = ∞ = I = ε R e q = 42 14 = 3,0   A .

    Passo 4

    c) Qual é a carga final do sobre o capacitor?

    Para um capacitor, temos a seguinte expressão:

    V c = q C

    A carga no capacitor é máxima quando   t = ∞ , então a carga máxima será dada por:

    q t = ∞ = Q = C V c

    Como nesse instante não passa corrente no trecho onde está o capacitor, ele está à mesma diferença de potencial que está o resistor R b c .

    Podemos escrever a diferença de potencial nesse ressitor como:

    V b c = R b c I

    E como V c = V b c , podemos substituir essa expressão na expressão para a carga do capacitor:

    q t = ∞ = Q = C V b c = C R b c I

    Como:

    R b c = 6   Ω

    C =   4 × 10 - 6   F

    I = i t = ∞ = 3,0   A  

    Lembrando que temos que utilizar a corrente quando t = ∞ porqeu é nesse momento que a carga no capacitor é máxima.

    Logo:

    Q = 4 × 10 - 6 × 6 × 3 = 7,2   ×   10 - 5   C .

    Se você entender bem este Exercício de fixação e outros parecidos que a gente resolve com você aqui, vai conseguir matar um monte de problemas desse tipo, vai por mim... ;-)

    Resposta

    1. i t = 0 = 4,2   A ;
    2. i t = ∞ = I = 3,0   A ;
    3. q t = ∞ = Q = 7,2   × 10 - 5 C .

    Exercício Resolvido #6

    Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 26.47, pp. 196.

    No circuito indicado na figura abaixo, os capacitores estão inicialmente descarregados, a bateria não possui resistência interna e o amperímetro é ideal. Ache a leitura do amperímetro:

    1. Logo após a chave S ser fechada;

    2. Após a chave estar fechada há muito tempo.

    Passo 1

    Você deve estar olhando para essa figura e se perguntando: “Pô, perae, você acabou de me mostrar uma teoria de um circuito RC simplizinho de uma malha, que eu consegui entender, e agora me vem com esse exercício com um monte de malhas, com um monte de resistores e capacitores distribuídos na maior loucura...deve tá de brincadeira comigo, né?”

    CALMA, muita calma nessa hora...kkk Vou te mostrar que esse problema se reduz a um problema de associação de resistores em série e em paralelo...Duvida? Continua sem desanimar, que você vai ver...

    Antes, quero discutir algumas coisas rápidas aqui com você. Olha só, você viu que se o capacitor está descarregado em t = 0 , então ele não tem carga nenhuma: q t = 0 = 0 . Bom, se não tem carga alguma no capacitor, isso significa que a diferença de potencial V c ( t = 0 ) entre as suas placas é

    V c t = 0 = q t = 0 C = 0 .

    Por outro lado, para um tempo muito grande, ou seja, t → ∞ , o capacitor fica totalmente carregado e nenhuma corrente flui mais através dele: i t → ∞ = 0 . Quase lá, quase... Essas duas características que comentei são FUNDAMENTAIS para você mater esse exercício...Dá uma olhada nelas de novo antes de seguir pro próximo passo!!

    Passo 2

    a) Agora, vamos colocar essas informações dos capacitores para t = 0 lá no circuito da figura. Então, olha só, o potencial entre os pontos a e b da figura é V a b = 0 . Isso significa que nenhuma corrente passa no resistor que está em paralelo a esse capacitor entre os pontos a e b , que é R a b = 25,0   Ω , mas passa corrente pelo capacitor C a b = 15,0   μ F . Por isso, podemos “eliminar esse resistor” do circuito para t = 0 .

    Podemos dizer o mesmo do resistor entre os pontos f e g , R f g = 25,0   Ω , que está em paralelo a outro capacitor. Bom, eliminamos, SEM NENHUMA CONTA, os resistores R a b e R f g ! \0/ \0/

    CUIDADO: o resistor R d e = 50,0   Ω não pode ser eliminado, pois está em série com o capacitor C c d = 20,0   μ F e por esse capacitor passa uma corrente. FICA DE OLHO...

    Como V a b = V c d = V f g = 0 , nosso circuito da figura pode ser simplificado para:

    Então, o resistor R d e está em paralelo com o resistor R g h e o resistor equivalente dessa associação, que é

    R 1 = R d e R g h R d e + R g h

    ( R 1 = 50 3   Ω ) está em série com os resistores R b c = 75,0   Ω e R e s = 15,0   Ω . A resistência total equivalente fica como

    R e q = R 1 + 75 + 15 = 320 3   Ω .

    A corrente i t = 0 é

    i t = 0 = 100 R e q = 300 320 ≈ 0.94   A .

    Passo 3

    b) E agora para t → ∞ ? Bom, para esse caso, não passa nenhuma corrente pelos capacitores, então não passa corrente pelo trecho do circuito entre os pontos   c e e da figura. Isso significa que podemos “eliminar esse trecho do circuito” para analisar a corrente i ( t = ∞ ) e também desconsiderar em nossa análise os outros capacitores também.

    Sobra o quê, então? Resta o seguinte circuito bem mais simples:

    Advinha o que vamos usar agora para saber qual a resistência equivalente? Associação de resistores em série, que nesse caso:

      R e q = 25 + 75 + 25 + 25 + 15 = 165   Ω  

    Feliz ou não??

    Agora, para fechar, a corrente para t = ∞ é

    i t = ∞ = 100 165 ≈ 0,61   A .

    Fica atento, porque esse tipo análise de circuitos R C para os instantes t = 0 e t = ∞ cai com bastante frequência nas provas…Fica de olho ;-) e pratica…

    Resposta

    1. i t = 0 ≈ 0,94   A ;

    2. i t = ∞ ≈ 0,61   A .

    Exercícios de Livros Relacionados

    O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
    O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
    Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
    No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
    A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67