Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Corrente Elétrica

Ver Todos os Exercícios

Teoria

Fala aí, nós somos o Responde Aí, a maior plataforma de exatas do Brasil, criada para ajudar você a ter um ensino didático e a mandar super bem na sua prova da faculdade.

Hoje nosso papo é sobre a corrente elétrica. Partiu?

O que é corrente elétrica?

A corrente elétrica é definida como o movimento de cargas elétricas, mais especificamente o movimento dos elétrons, no interior de materiais condutores. Ela é a grandeza física que nos permite saber a quantidade de carga que atravessa em condutor a cada segundo.

Fórmula da Corrente Elétrica

Pensando no que falamos anteriormente, que a corrente elétrica é a grandeza física que nos permite saber a quantidade de carga que passa a cada segundo, podemos definir, matematicamente, a corrente elétrica através da seguinte fórmula:

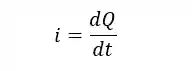
Fórmula da Corrente Elétrica
Fórmula da Corrente Elétrica

Onde:

  • é a corrente elétrica;
  • é a carga elétrica, expressa em ;
  • é o tempo, expresso em , e;
  • é a taxa de variação da carga com relação ao tempo, que é exatamente a definição de corrente elétrica.

Observação importante: A corrente elétrica tem unidade de carga por tempo, ou seja . A essa unidade damos o nome de è. Então, no Sistema Internacional de medidas (SI), a corrente é medida em é.

Uma boa dica é você escarar a corrente como se ela fosse uma espécie de velocidade.

É bom a gente lembrar também a fórmula da variação de carga, que é dada por:

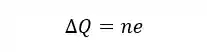
Fórmula da Variação de Carga
Fórmula da Variação de Carga

Onde:

  • é a variação de carga;
  • é o número de portadores de carga, ou seja, o número de elétrons que passaram, e;
  • é a a carga elementar, ou seja, a carga de um único elétron. Seu módulo vale aproximadamente

Podemos ainda construir um gráfico de corrente versus tempo e a área desse gráfico nos fornecerá a variação de carga:

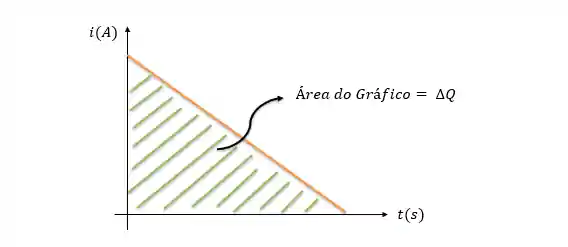
Gráfico de corrente
Gráfico de corrente

Sentido da Corrente Elétrica

Mais uma coisa que você precisa saber sobre a corrente elétrica é que ela possuiu um sentido. Se você olhar um circuito de cima, você pode ver a corrente no sentido horário ou no sentido anti-horário.

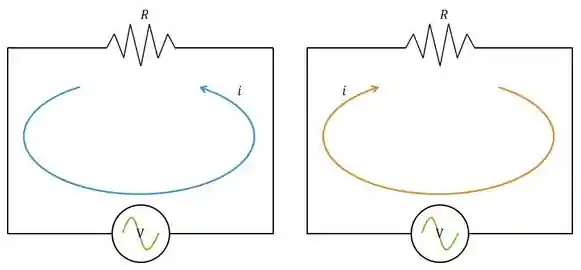
Possíveis sentidos da corrente elétrica: anti-horário e horário, respectivamente.
Possíveis sentidos da corrente elétrica: anti-horário e horário, respectivamente.

Uma informação hiper mega importante sobre esse sentido da corrente: Ele é arbitrado como sendo o sentido em que as cargas positivas se moveriam, que por sinal é contrário ao sentido de movimento das cargas negativas (elétrons). Sendo assim, se você tem que os elétrons se movem em sentido horário, a corrente estará no sentido anti-horário. Sacou? É sempre o contrário.

Um alerta aqui pra você: Embora nós representemos uma corrente elétrica com uma seta indicando o seu sentido, ela é uma grandeza escalar. Então, nem pense em colocar a corrente elétrica como um vetor, estamos entendidos?

Corrente Elétrica e Circuitos Elétricos

Provavelmente, você vai se deparar nos exercícios com situações em que uma única corrente elétrica ao chegar em determinado ponto do circuito encontra dois ou mais caminhos para seguir (chamamos esse ponto de nó) e assim ela se divide em outras correntes, como mostra essa figura aqui:

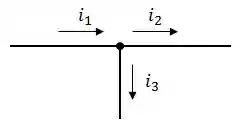
Exemplo de circuito com divisão de correntes elétricas.
Exemplo de circuito com divisão de correntes elétricas.

Para esses casos, existe uma Lei, chamada de Lei dos nós de Kirchhoff que diz que a soma das correntes que entram é igual a soma das corrente que saem. Sendo assim, para a figura mostrada a cima teremos:

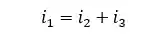
Lei dos nós de Kirchhoff
Lei dos nós de Kirchhoff

E a gente finaliza por aqui o conteúdo sobre corrente elétrica. Curtiu?

A partir daqui você pode avançar nos seus estudos e ir conferir o nosso próximo tópico: Densidade de Corrente Unifome. Ou você pode querer fixar ainda mais o conceito de corrente elétrica, e pode fazer isso através do vídeo que eu vou deixar aqui em baixo 👇🏾, feito por nós do Responde Aí, para você aprender de forma rápida e eficaz.

Vídeo

Exercícios Resolvidos

Exercício Resolvido #1

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-1

Durante os 4,0   m i n em que uma corrente de 5,0   A atravessa um fio, a Quantos coulombs e b quantos elétrons passam por uma seção reta do fio?

Passo 1

a Quantos coulombs passam por uma seção reta do fio?

Por definição, a corrente é dada por:

i = d q d t

Como a corrente é constante, podemos dizer que:

i = Δ q Δ t

Assim, a quantidade de coulombs será:

Δ q = i Δ t

O que precisamos ter em mente aqui é que o tempo deve estar em segundos, logo:

Δ t = 4 × 60 = 240   s

Finalmente:

Δ q = 5 × 240

Δ q = 1200   C

Passo 2

b Quantos elétrons passam por uma seção reta do fio?

A carga total dos elétrons que passam pela seção reta do fio deve ser igual a 1200   C , logo:

Δ q = n e

Como já vimos, n é o número de elétrons e e é a carga elementar, que vale aproximadamente e = 1,6 × 10 - 19 C .

n = Δ q e

n = 1200 1,6 × 10 - 19

n = 7,5 × 10 21  

Resposta

a

Δ q = 1200   C

b

n = 7,5 × 10 21  

Exercício Resolvido #2

Universidade Estadual de Londrina

Pela secção reta de um condutor de eletricidade passam 12,0   C a cada minuto. Nesse condutor, a intensidade da corrente elétrica, em ampères, é igual a:

a) 0,08 b) 0,20 c) 5,00 d) 7,20 e) 120

Passo 1

Vimos que i = ∆ q ∆ t .

O enunciado fala que em 60   s passam 12   C , então

i = 12 60 = 0,2   A

A alternativa correta portanto é a letra B :)

Resposta

b) 0,20

Exercício Resolvido #3

Universidade Estadual do Maranhão

Uma corrente elétrica com intensidade de 8,0   A percorre um condutor metálico. A carga elementar é e = 1,6 × 10 - 19   C . Determine o tipo e o número de partículas carregadas que atravessam uma secção transversal desse condutor, por segundo, e marque a opção correta:

a) Elétrons; 4 × 10 19 partículasb) Elétrons; 5 × 10 19 partículasc) Prótons; 4 × 10 19 partículasd) Prótons; 4 × 10 19 partículase) Prótons num sentido e elétrons no outro; 5 × 10 19 partículas

Passo 1

Antes de tudo, como o condutor é metálico, já sabemos que as partículas que formam a corrente são os elétrons.

Pra calcular o número de partículas, primeiro vamos usar i = ∆ q ∆ t para encontrarmos ∆ q e aplicarmos em ∆ q = n e , e por fim encontrarmos n .

Passo 2

Sabendo que em 1 segundo temos 8   A :

8 = ∆ q 1

∆ q = 8   C

Agora é só encontrar o n :

8 = n × 1,6 × 10 - 19

n = 5 × 10 19

A alternativa correta é a letra b :D

Resposta

b) Elétrons; 5 × 10 19 partículas

Exercício Resolvido #4

Elaboração própria.

Com base no circuito abaixo, onde R 1 ≠ R 2 ≠ R 3 , considere as afirmações a seguir

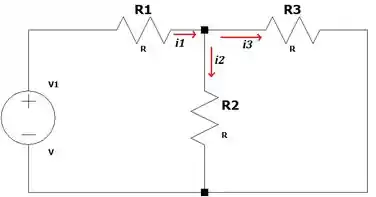
I) i 2 > i 1

II) i 3 = i 1 - i 2

III) Se i 1 = 0 , i 2 = i 3

Quais afirmações estão corretas?

a) Apenas I

b) Apenas II

c) Apenas III

d) I e II

e) II e III

Passo 1

Vamos analisar cada uma das afirmativas:

  1. i 2 > i 1

    2. Bom, sabemos que a corrente i 1 será dividida nas corrente i 2 e i 3 , portanto:

    i 1 = i 2 + i 3

    Logo, é matematicamente impossível que a corrente i 2 seja maior que a corrente i 1 , logo essa é falsa.

    Passo 2

  2. i 3 = i 1 - i 2

    3. Como dito no Passo 1, a corrente será:

    i 1 = i 2 + i 3

    Logo, isolando i 3 teremos:

    i 3 = i 1 - i 2

    E essa alternativa está correta.

    Passo 3

  3. Se i 1 = 0 , i 2 = i 3

Nesse caso, para a corrente i 1 ser zero é necessário que não haja corrente circulando no circuito, o que faria com que:

i 1 = 0 ,   i 2 = 0 ,   i 3 = 0

E assim, as correntes i 2 e i 3 são iguais, portanto, esta também está correta.

Portanto, a alternativa correta é a letra e .

Resposta

e) II e III

Exercício Resolvido #5

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-2

Uma esfera condutora isolada tem 10   c m de raio. Um fio leva até ela uma corrente de 1,0000020   A . Outro fio retira dela uma corrente de 1,0000000   A .

Quanto tempo é necessário para que o potencial da esfera aumente de 1000   V ?

Dados:

ϵ 0 = 8,85 × 10 - 12   C 2 / N m 2

Passo 1

Como a corrente que chega na esfera é maior que a corrente que sai da esfera, haverá uma taxa de aumento de carga na esfera dada por:

Δ i = 1,0000020 - 1,0000000

Δ i = 0,000002 C s

Como essa taxa é constante, podemos dizer que:

Δ q Δ t = 0,000   002 C s

Δ q = 0,000002 Δ t

Passo 2

Como a esfera é condutora, as cargas elétricas estão todas na sua superfície. Assim, o potencial elétrico da esfera é dado por:

V = q 4 π ϵ 0 r  

Logo, a variação de potencial elétrico será:

Δ V = Δ q 4 π ϵ 0 r

Substituindo a expressão que encontramos no Passo 1:

Δ V = 0,000002 Δ t 4 π ϵ 0 r

Reorganizando esses dados, teremos:

Δ t = 4 π ϵ 0 . Δ V . r 0,000002

Onde:

ϵ 0 = 8,85 × 10 - 12   C 2 / N m 2

Δ V = 1000   V

r = 10   c m = 0,1   m

Finalmente:

Δ t = 4 π × 8,85 × 10 - 12 × 1000 × 0,1 0,000002

Δ t = 5,56 × 10 - 3 s

Δ t = 5,56   m s

Resposta

Δ t = 5,56   m s

Exercício Resolvido #6

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 164-55. Modificada

Um feixe de partículas alfa q = + 2 e com uma energia cinética de 20   M e V corresponde a uma corrente de 0,25   μ A .

a Se o feixe incide perpendicularmente em uma superfície plana, quantas partículas alfa atingem a superfície em 3,0 s ?

b Qual é a diferença de potencial necessária para acelerar as partículas alfa, a partir do repouso, para que adquiram uma energia de 20   M e V ?

Passo 1

Nossa meta aqui será encontrar a variação da carga das partículas alfa e relaciona-la com o número de partículas.

Pro elétron essa relação era:

∆ q = n e

E aqui o que muda será que:

∆ q = 2 n e

Onde n é o número de partículas que queremos encontrar.

Não é relevante o sinal das partículas aqui, mas sim sua quantidade em módulo.

Passo 2

a Se o feixe incide perpendicularmente em uma superfície plana, quantas partículas alfa atingem a superfície em 3,0 s ?

Como temos uma corrente constante, podemos dizer que:

i = Δ q Δ t

E daqui poderemos tirar a variação da carga.

∆ q = i ∆ t

Convertendo a corrente para o sistema internacional temos:

i = 0,25   μ A = 2,5 × 10 - 7   A

Agora é só substituir e achar ∆ q :

∆ q = 2,5 × 10 - 7 × 3

∆ q = 7,5 × 10 - 7   C

Calculando a quantidade de carga que passou conforme o tempo, poderemos comparar com a carga de uma partícula e daí descobriremos quantas partículas alfa temos:

Δ q = 2 n e

Lembrando que a constante e possui o seguinte valor:

e = 1,6 × 10 - 19   C

Isolando a quantidade de partículas alfa n temos:

n = ∆ q 2 e

Substituindo os valores:

n = 7,5 × 10 - 7 2 × 1,6 × 10 - 19

n = 2,3 × 10 12

A carga total que incide na superfície plana será:

Δ q = n q

Passo 3

b Qual é a diferença de potencial necessária para acelerar as partículas alfa, a partir do repouso, para que adquiram uma energia de 20   M e V ?

O sistema inicialmente está em repouso e não é inserido nenhum impulso nele, portanto a energia mecânica se conserva e aí aplicamos o teorema da conservação de energia:

∆ U + ∆ E C = 0

A energia potencial da carga é dada por:

∆ U = q ∆ V

Assim:

q ∆ V = - ∆ E C

∆ V = - ∆ E C q

Por fim, substituindo os valores temos:

Δ V = - 20   M e V 2 e

Δ V = - 10   M V

E é isso! Mais um pra conta.

Resposta

a

2,3 × 10 12

b

Δ V = - 10   M V

Exercício Resolvido #7

Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 25, pp.172

Durante um raio de uma nuvem até o solo, podem ocorrer correntes de até 25.000   A , que duram cerca de 40   μ s . Quanta carga é transferida da nuvem para a terra durante um raio?

Passo 1

A definição de corrente é dada por:

i = d q d t ,

mas vamos considerar a corrente constante nesse caso. Temos, então:

i = Δ q Δ t .

Passo 2

A quantidade de carga transferida será:

Δ q = i Δ t .

Substituindo os valores i = 25.000   A e Δ t = 40   μ s , temos:

Δ q = 25.000 × 40 × 10 - 6 ,

Δ q = 1   C .

Resposta

Δ q = 1   C .

Exercício Resolvido #8

Elaboração própria

No circuito da figura abaixo, sabemos os valores das correntes I 1 = 5   A , I 2 = 1   A e I 5 = 3   A .

Quais os valores das correntes I 3 e I 4 ?

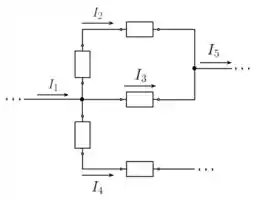
Passo 1

Aqui, vamos usar a Lei dos nós de Kirchhoff para calcular as correntes I 3 e I 4 , que diz que a soma das correntes que chegam é igual à soma das correntes que saem.

Bem, e por onde começar? Vamos olhar para cada um dos nós do circuito e aplicar a lei. Temos, para o primeiro nó:

I 1 = I 2 + I 3 + I 4

e para o segundo:

I 2 + I 3 = I 5 .

Passo 2

Agora precisamos substituir os valores I 1 = 5   A , I 2 = 1   A e I 5 = 3   A :

5 = 1 + I 3 + I 4 → I 3 + I 4 = 4   A ,

para o primeiro nó e

1 + I 3 = 3 → I 3 = 2   A ,

para o segundo.

Logo,

I 4 = 4 - I 3 = 2   A .

Resposta

I 3 = 2   A e I 4 = 2   A .

Exercícios de Livros Relacionados

Enquanto você está reformando sua garagem, você precisa emendar temporariamente um fio de cobre de 80 m de comprimento e 1,00 mm de diâmetro com um fio de alumínio de 49 m de comprimento, que tem o me
A Figura 20.13 mostra um cone feito de material com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e forma metalizadas. Supondo
Mostre que a resistência elétrica de uma placa quadrada de espessura fixa, para correntes paralelas a uma de suas arestas, independe do tamanho da placa.
Seguindo o procedimento análogo ao do 20.6P, calcule a constante de tempo de um capacitor esférico preenchido por um dielétrico.
A Figura 20.12 mostra um capacitor cilíndrico preenchido por um material dielétrico de resistividade elétrica ρ e constante dielétrica κ . Uma bateria aplica uma voltagem V ao capacitor.a) Calcule a c