Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Campo Elétrico Gerado por uma Linha de Cargas

Ver Todos os Exercícios

Teoria

Campo Elétrico Gerado por Linha de Cargas

Hora da ação! Vamos imaginar um fio de comprimento 2 a , positivamente carregado. Você sabe dizer qual o valor do campo elétrico gerado por ele no ponto P ?

Não sabe? Relaxa, vou te ensinar agora!

Se quisermos achar o campo elétrico resultante num ponto arbitrário no eixo x , basta nós somarmos todos os campos de todas as partículas infinitesimais de carga d q que compõem a barra:

d E → = k d q r 2 r ^

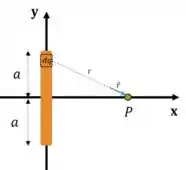
Mas antes da gente pensar em fazer integrais aqui, vamos decompor o nosso vetor d E → , mas é necessário decompor em dois eixos?

A simetria da figura vai ajudar a gente a responder isso, se liga que isso facilita bastante as contas!

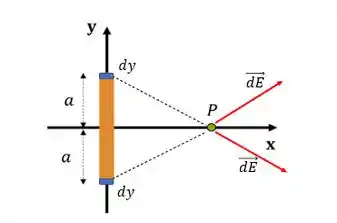
Se a gente só desenhar o campo elétrico decomposto nas duas direções no ponto P vamos perceber o seguinte:

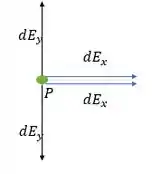
No eixo y os campos apontam em direções opostas e se anulam então a gente só vai ter campo elétrico no eixo x .

E → = E x i ^

Voltando pra decomposição temos:

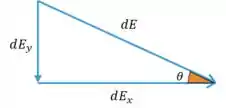
“Ué, não ia decompor o r ^ ?” Sim, mas dá no mesmo decompor o d E → pois afinal de contas ele aponta na direção de r ^ . Então:

d E x = d E cos ⁡ θ

Ok, agora basta conectar esses seno e cosseno com a geometria do problema, certo? Observando a figura:

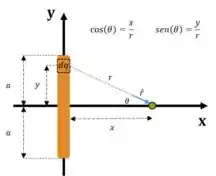
E nos utilizando do fato de que, por Pitágoras:

r = x 2 + y 2

Podemos substituir:

cos ⁡ θ = x x 2 + y 2

E temos que:

d E = k d q x 2 + y 2

Portanto:

d E x = k d q x 2 + y 2 x x 2 + y 2

Se a gente tivesse componente na vertical também teríamos que decompor em y mas aí era só pegar a equação e trocar x   por y .

d E y = k d q x 2 + y 2 y x 2 + y 2

Putz mas e agora, como que vamos integrar pra d q , se o que varia na verdade é o comprimento y ?

A gente usa a densidade linear de carga pra relacionar esses caras!

λ = d q d y

Isolando d q :

d q = λ d y

Podemos agora substituir e integrar:

d E x = k λ d y x 2 + y 2 x x 2 + y 2

E a gente tem que integrar ao longo de todo o fio, ou seja, de - a até a .

E x = ∫ - a a k λ d y x 2 + y 2 x x 2 + y 2

Como k é constante fica pra fora e rearrumando a raiz embaixo temos enfim:

E x = k λ x ∫ - a a d y x 2 + y 2 3 2

Calma aí, antes de infartar com essa integral posso te tranquilizar dizendo que geralmente os formulários de prova dão o resultado dela, o que é cobrado é o caminho de chegar nela. Então se você chegou até aqui é um vencedor haha! O resultado dela fica algo mais ou menos assim:

E x = k λ y x 2 + y 2   | - a a

E x = k λ a x 2 + a 2 - λ - a x 2 + a 2 = 2 k λ a x 2 + a 2

Enfim ficaria:

E → = E x i ^

E →   = 2 k λ a x 2 + a 2 i ^

Campo Elétrico Gerado por um Anel Carregado

A gente já viu como que funciona o campo elétrico de uma linha de cargas, mas e no caso de um anel carregado, como encontrar esse campo num ponto P se o anel é totalmente carregado por cargas positivas?

A equação do campo elétrico continua sendo verdade:

d E → = k d q r 2 r ^

Vamos desenhar a geometria da figura e analisar algumas coisas.

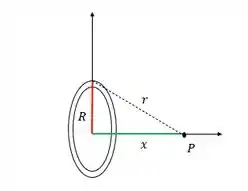
Daqui da figura a gente consegue ver que o valor de r por Pitágoras é:

r = R 2 + x 2

E agora é a hora de decompor os campos nas duas direções, mas de novo, é bom olhar a simetria do problema e analisar se vamos precisar mesmo.

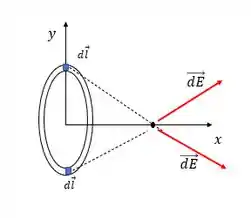
Repara o seguinte, como as cargas são todas positivas a simetria é do mesmo jeito que rolou com a linha de cargas. Ao pegarmos dois infinitesimais d l → a gente vê que de novo nesse caso teremos que:

E → = E x i ^

Então faremos só a decomposição pra x e pra isso a gente pode usar a mesma figura da linha de cargas já que as posições são parecidas.

d E x = d E × x r

d E x = k d q r 2 × x r  

d E x = k d q r 3 x

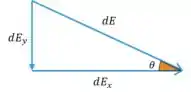
E com o valor de r teremos:

d E x = k d q x R 2 + x 2 3

E os

E x = ∫ A n e l k d q x R 2 + x 2 3

E aqui a gente pode retirar as constantes e deixar na integral apenas a carga, e aqui faremos com a integral o somatório de todas as cargas d q ao longo do anel.

E x = k x R 2 + x 2 3 ∫ A n e l d q

Integrando todos os pedaços infinitesimais de cargas no anel, teremos a carga total no anel:

∫ A n e l d q = Q

Portanto a expressão do campo vai ficar:

E x = k x Q ( x 2 + R 2 ) 3 2

E se fosse pedida a densidade linear de carga λ , basta fazer:

d q = λ d l

Integrando os dois lados, sendo que o comprimento total vai ser o comprimento do anel temos:

Q = λ × 2 π R

Você também pode escrever a constante k da seguinte forma:

k = 1 4 π ε 0

O que daria:

E x = 1 4 π ε 0   . Q x ( x 2 + R 2 ) 3 2

Pra finalizar podem aparecer casos em que x ≫ R então o campo elétrico ficaria:

E → = k Q x x 3

E o contrário também rola quando R ≫ x .

E → = k Q x R 3

É isso, partiu exercícios?

Campo Elétrico Gerado por um Anel Carregado

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 45-24.

Na figura abaixo, uma barra fina de vidro forma uma semicircunferência de raio r = 5,00   c m .

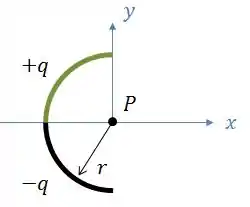
Uma carga + q = 4,5   p C está distribuída uniformemente na metade superior da barra, e uma carga - q = - 4,5   p C está distribuída uniformemente na metade inferior.

Determine:

  1. O módulo do campo elétrico E → no ponto P , situado no centro do semicírculo.
  2. A orientação (em relação do semi-eixo x positivo) do campo elétrico E → no ponto P , situado no centro do semicírculo.

Passo 1

Nesse tipo de problemas, a malandragem é explorar, logo de cara, a simetria do problema.

Vou começar fazendo o seguinte: vou pegar dois pontos simétricos e ver qual seria o campo elétrico resultante no ponto P , decompondo o campo elétrico E → em componentes E x →   e E y → .

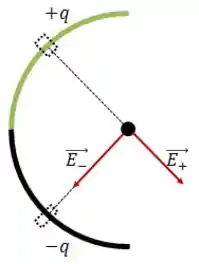
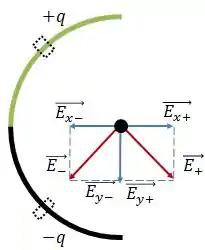
Tá vendo que as componentes em x vão se anular e as componentes em y vão se somar?

Então, o campo elétrico resultante vai ser algo do tipo:

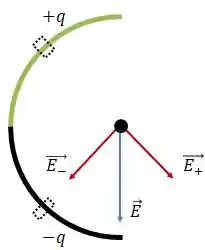
Show de bola! Essa interpretação facilita a nossa vida porque não precisamos mais nos preocupar com uma componente horizontal desse campo elétrico.

A figura mostra também que os dois arcos produzem o mesmo campo elétrico na vertical. Assim, só precisamos calcular um deles.

Passo 2

A contribuição d E devido a um elemento de carga d q da haste superior é dada por:

d E = 1 4 π ε 0 d q r 2

Sabendo que a carga é distribuída uniformemente ao longo da haste, podemos dizer que:

d E = 1 4 π ε 0 λ   d s r 2

Onde λ é a densidade linear de carga. Sabendo também que se trata de um arco, podemos dizer que d s = r   d θ , onde θ vai variar de 0 a π / 2 . Portanto:

d E = 1 4 π ε 0 λ r   d θ r 2

Entretanto, como estamos interessados somente na componente vertical, vamos precisar decompor esse campo d E , assim como fizemos antes:

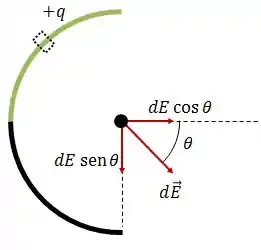
Portanto:

d E y = 1 4 π ε 0 λ sen ⁡ θ   d θ r

Agora sim, agora estamos falando a minha língua!

Pra calcular o campo elétrico resultante da haste superior, basta integrar isso aqui:

∫ d E y = 1 4 π ε 0 λ   r ∫ 0 π / 2 sen ⁡ θ   d θ  

E y = 1 4 π ε 0 λ   r   - cos ⁡ θ 0 π / 2

E y = 1 4 π ε 0 λ   r

Sabendo que λ é a densidade linear de carga, podemos dizer que:

λ = q π r / 2 = 2 q π r

Substituindo de volta:

E y = 1 4 π ε 0 2 q π r 2  

E y = q 2 π 2 ε 0 r 2

Eita! Eu sei, foi tenso... mas só falta um detalhe pra terminar, juro!

Passo 3

Acontece que calculamos somente o campo elétrico da parte positiva da haste. Mas como sabemos que o campo vertical produzido pela parte negativa vai ser igual, baste dizer que:

E = 2 E y

Logo:

E = q π 2 ε 0 r 2

Agora sim, acabou!

Ah! Caso você tenha usado k ao invés de 1 / 4 π ε 0 , o resultado que você vai encontrar vai ser

E = 4 k q π r 2

Relaxa, as duas respostas estão certas.

Agora só temos que substituir os valores!

Passo 4

E = 4 k q π r 2

Onde:

k ≅ 9 × 10 9   N m 2 C - 2 ;

q = 4,5   p C = 4,5 × 10 - 12   C ;

r = 5,00   c m = 5 × 10 - 2 m ;

π ≅ 3,14 ;

Logo:

E = 4 × 9 × 10 9 × 4,5 × 10 - 12 3,14 × 5 × 10 - 2 2

E = 20,63   N / C

Resposta

  1. E = 20,63   N / C

  2. O campo é vertical, apontando para baixo (sentido - y ).

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 47-33.

Na figura abaixo, uma barra não condutora “semi-infinita” (ou seja, infinita apenas em um sentido) possui uma densidade linear de cargas uniforme λ .

Mostre que o campo elétrico E P → no ponto P faz um ângulo de 45 ° com a barra e que esse resultado não depende da distância R .

(Sugestão: Calcule separadamente as componentes de E P → nas direções paralela e perpendicular à barra.)

Passo 1

Ok, vamos seguir a sugestão do problema!

Obs: Nesse tipo de problema, calcular as componentes separadamente é sempre o melhor caminho, então guarda isso contigo!

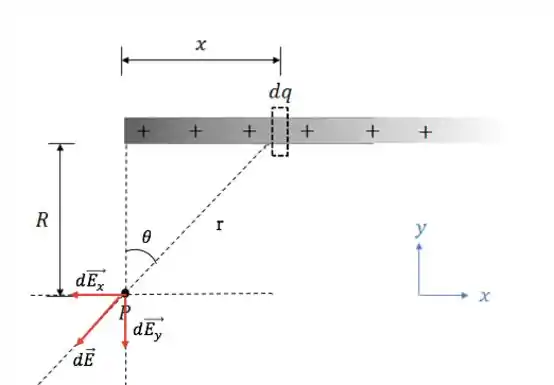
Pra fazer isso, vamos pegar um pedaço infinitesimal da barra com carga d q e calcular as componentes do campo elétrico gerado por ela ( d E x e d E y ) no ponto P .

Olhando a figura, podemos dizer que

d E x = - d E sen ⁡ θ = - d q 4 π ε 0 r 2 sen ⁡ θ

d E y = - d E cos ⁡ θ = - d q 4 π ε 0 r 2 cos ⁡ θ

Sabemos ainda que:

d q = λ d x

Logo:

d E x = - λ d x 4 π ε 0 r 2 sen ⁡ θ

d E y = - λ d x 4 π ε 0 r 2 cos ⁡ θ

Nessas equações, tanto x quanto r quanto θ vão variar quando formos integrar, então precisamos deixar tudo em função de uma única variável.

Passo 2

Vamos lá! Temos que relacionar θ ,   r e x . Como podemos fazer isso?

Bom, pela figura, podemos chegar que:

c o s θ = R r → r = R c o s θ

t g   θ = x R → x = R   t g θ → d x = R s e c θ 2 d θ = R c o s θ 2 d θ

Substituindo esses resultados em nossas equações de d E x e d E y :

d E x = - λ R 4 π ε 0 R c o s θ 2 c o s θ 2 sen ⁡ θ = - λ 4 π ε 0 R sen ⁡ θ d θ

d E y = - λ d x 4 π ε 0 r 2 cos ⁡ θ = - λ 4 π ε 0 R cos ⁡ θ d θ

Passo 3

Último passo, galera!!

Agora, temos que integrar. Como queremos pegar a barra toda e ela é semi-infinita, vamos integrar com θ variando de 0 a π / 2 :

d E x = - λ 4 π ε 0 R sen ⁡ θ d θ

E x = - λ 4 π ε 0 R ∫ 0 π 2 sen ⁡ θ d θ = λ 4 π ε 0 R cos ⁡ π 2 - cos ⁡ 0 = λ 4 π ε 0 R 0 - 1

E x = - λ 4 π ε 0 R

E o campo na direção y fica

d E y = - λ 4 π ε 0 R cos ⁡ θ d θ

E y = - λ 4 π ε 0 R ∫ 0 π 2 cos ⁡ θ d θ = - λ 4 π ε 0 R s e n π 2 - s e n 0 = - λ 4 π ε 0 R 1 - 0

E y = - λ 4 π ε 0 R

Percebemos, então que E x = E y , independente do valor de R . Logo, temos que o ângulo entre o campo e a barra é θ = 45 ° .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 45-23.

A figura abaixo mostra dois anéis não condutores paralelos, com os centros sobre a mesma reta perpendicular aos planos dos anéis. O anel 1 , de raio R , possui uma carga uniforme q 1 ; O anel 2 , também de raio R , possui uma carga uniforme q 2 ; Os anéis estão separados por uma distância d = 3 R . O campo elétrico no ponto P situado na reta que passa pelos centros dos anéis a uma distância R do anel 1 é zero. Determine a razão q 1 / q 2 .

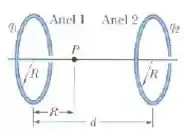
Passo 1

Primeiramente, vamos pensar em pedacinhos de carga opostos no anel e no campo elétrico que eles causam em um ponto P no eixo do anel:

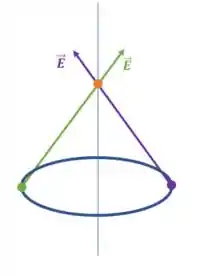
Esses pedacinhos de carga representados pelos pontos verde e roxo no anel geram dois vetores de campo elétrico. Vamos olhar esses dois vetores mais de perto:

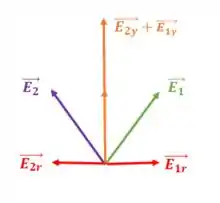
Você percebe comigo que decompondo esses vetores na direção do raio do anel ( E 1 r →   e   E 2 r → ) , eles terão o mesmo módulo e direções opostas, ou seja, se cancelam. Enquanto as componentes na direção da reta do ponto P ( E 1 y →   e   E 2 y → ) , como temos vetores na mesma direção, teremos a soma de seus módulos.

Dessa forma pela simetria do problema, que o campo elétrico resultante E R se encontra sobre o eixo que liga os centros dos dois anéis, que chamaremos de X . Assim:

E R = E X

Passo 2

O campo resultante em P deverá ser zero. Como cada um está de um lado diferente do ponto P , a diferença entre os campos deverá ser nula:

E X 1 - E X 2 = E X = 0 → E X 1 = E X 2

Passo 3

A nossa estratégia aqui vai ser a seguinte: vamos começar calculando a contribuição infinitesimal de cada pedacinho dos anéis, em cada anel, na determinação do campo elétrico total. Começando pelo primeiro anel:

d E 1 = K . d q 1 D 1 2

A distâncias D 1 é a distância de um ponto qualquer do primeiro anel ao ponto P . Como podemos ver na figura abaixo:

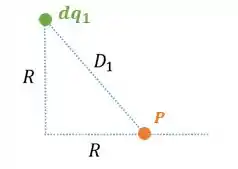
Por ser um triângulo retângulo, sabemos que a distância D 1 é igual a:

D 1 = R 2 + R 2 = 2 R

Passo 4

Pela mesma figura, podemos projetar cada o campo d E 1 no eixo de simetria X , para encontrar d E X 1 :

d E 1 X = d E 1 . c o s θ 1 = d E 1 . R D 1

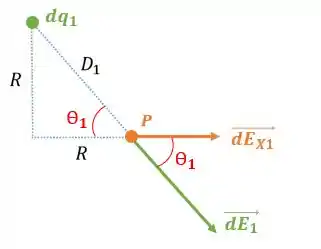
Como sabemos que D 1 = 2 R   :

d E 1 X = d E 1 . 1 2

Substituindo d E 1 =   K . d q 1 D 1 2 :

d E 1 X =   K . d q 1 D 1 2 . 1 2

d E 1 X =   K . d q 1 2 R 2 . 1 2

Para encontrar o módulo do campo E 1 X , vamos integrar:

E 1 X = ∫ K 2 2 R 2 d q 1 = K 2 2 R 2 . ∫ d q 1 = K q 1 2 2 R 2

Pronto, um campo elétrico já foi! Vamos repetir o processo para o outro anel!

Passo 5

Cada pedacinho infinitesimal de carga do anel 2 d q 2 irá gerar uma parcela do campo elétrico no ponto P igual a d E 2 :

d E 2 = K . d q 2 D 2 2

Onde D 2 é a distância entre o ponto P e essa carga infinitesimal do anel:

D 2 = R 2 + d - R 2

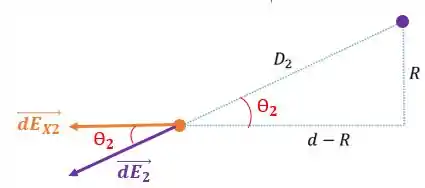
Como d = 3 R :

D 2 = R 2 + ( 3 R - R ) 2 = 5 R

Passo 6

Pela mesma figura, podemos projetar cada o campo d E 2 no eixo de simetria X .

d E 2 X = d E 2 . c o s θ 2

Percebemos que c o s θ 2 é igual a:

c o s θ 2 = d - R D 2 = 2 R 5 R = 2 5

Substituindo d E 2 e c o s θ 2 :

d E 2 X =   K . d q 2 D 2 2   . 2 5  

Como D 2 = 5 R , o módulo do campo d E 2 X :

d E 2 X = 2 K 5 5 R 2 d q 2

Boa! Agora só temos que integrar o campo infinitesimal encontrado:

E 2 X = ∫ 2 K 5 5 R 2 d q 2 = 2 K 5 5 R 2 . ∫ d q 2   = 2 K q 2 5 5 R 2

Passo 7

Pra fechar, basta igualar esses dois campos, conforme concluímos lá no Passo 2.

E 1 X = E 2 X

K q 1 2 2 R 2 = 2 K q 2 5 5 R 2

Cortando a constante K e o raio R :

q 1 q 2 = 4 . 2 5 5 = 0,506   ( a p r o x . )  

Resposta

0,506

Exercício Resolvido #4

PUCRIO-P1-2013.1-1- c

Uma barra delgada de comprimento L   [ m ] é envergada até formar um semi-círculo, conforme mostra a Figura 1.

a ) Se a barra tem uma densidade de carga uniforme λ > 0   [ C / m ] , calcule o campo elétrico na origem.

b ) Onde deveria ser colocada uma carga pontual de valor igual ao da carga total da barra para que o campo na origem fosse nulo?

c ) Considere agora que esse semicírculo se torne um semi-disco de mesmo raio com um orifício concêntrico semicircular de raio L / 10 π   [ m ] e com uma densidade superficial uniforme σ   [ C / m 2 ] , como mostrado na Figura 2. Calcule o campo elétrico na origem devido a esta nova configuração.

Passo 1

a )

Para calcular o campo elétrico na origem, devido a barra carregada, podemos usar a equação do campo gerado por uma carga infinitesimal:

d E → = k . d q r 2 r ^

Pela simetria, vemos que dois pontos simétricos em relação ao eixo y , produzem campos infinitesimais cujas componentes x irão cancelar, sobrando apenas as componentes y que estão se somando!

Então, queremos:

d E → . sen ⁡ θ = k . d q r 2 . sen ⁡ θ ( - y ^ )

No nosso caso, temos d q = λ . d l = λ . r . d θ , substituindo:

d E → . sen ⁡ θ = k . λ . r . d θ r 2 . sen ⁡ θ ( - y ^ )

Integrando:

E → y = k . λ r ∫ 0 π sen ⁡ θ d θ   ( - y ^ )

E → y = k . λ r ∫ 0 π sen ⁡ θ d θ   ( - y ^ )

E → y = k . λ r - cos ⁡ θ 0 π   ( - y ^ )

E → y = 2 k . λ r   ( - y ^ )

Onde π . r = L , logo:

E → y = 2 k . π . λ L   ( - y ^ ) [ N / C ]

Passo 2

b )

Para que o campo em P seja nulo, o campo gerado pela carga Q deve ser igual em módulo ao campo gerado pelo fio, e de sinal oposto para poder cancelá-lo. O campo gerado pela carga é dado por:

E → Q = k . Q y 2 R ^

Como a carga possui a mesma carga total da barra:

Q = λ . L

Substituindo e igualando ao valor do campo:

k . λ . L y 2 = 2 k . π . λ L

y 2 = L 2 2 . π

y = ± L 2 . π

A carga Q , por ter mesmo sinal que a barra, deve ser colocada no lado oposto, ou seja:

y = - L 2 . π  

Passo 3

c )

Para determinar o campo na origem, devido o disco carregado, podemos partir do que já calculamos no item a , para um semicírculo à uma distancia r da origem, temos que o campo gerado é:

d E → y = 2 k . σ r d r   ( - y ^ )

Integrando de r = L / 10 . π até r = L / π , temos:

E → y = ∫ L 10 π L π 2 k . σ r d r   ( - y ^ )

E → y = 2 k . σ ∫ L 10 π L π 1 r d r   ( - y ^ )

E → y = 2 k . σ ln ⁡ L π - ln ⁡ L 10 π   ( - y ^ )

E → y = 2 k . σ ln ⁡ 10   - y ^ [ N / C ]

Resposta

a ) E → y = 2 k . π . λ L   ( - y ^ ) [ N / C ]

b ) y = - L 2 . π  

c ) E → y = 2 k . σ ln ⁡ 10   - y ^ [ N / C ]

Exercício Resolvido #5

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 46-28.

A figura abaixo mostra dois anéis concêntricos de raios R e R ' = 3,00 R , que estão no mesmo plano. O ponto P está no eixo central Z , a uma distância D = 2,00 R do centro dos anéis. O anel menor possui carga uniforme distribuída Q . Em termos de Q , qual deve ser a carga uniformemente distrubuída no anel maior para que o campo elétrico no ponto P seja nulo?

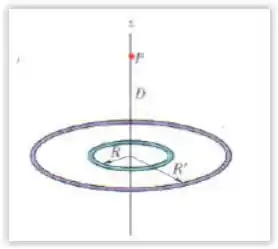
Passo 1

Notar a simetria do problema: o campo elétrico resultante E R está na direção Z , então, precisamos descobrir apenas qual é a componente desse campo nesta direção.

E R = E Z

Passo 2

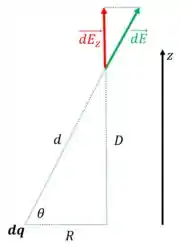
Calcular o campo elétrico que um pedaço do anel, com carga infinitesimal d q , exerce no ponto P :

d E = K . d q d 2

Onde d é a distância entre um ponto do anel e o ponto P como podemos ver na figura abaixo:

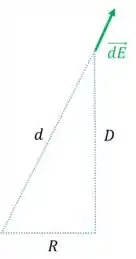
Passo 3

Calcular, pela geometria do problema, o valor de d 2 em função de R e de D :

d 2 = D 2 + R 2

Passo 4

Substituir na equação do segundo passo:

d E = K . d q D 2 + R 2

Passo 5

Olhar novamente o triângulo representado acima. Calcular a projeção do campo elétrico no eixo de simetria pela geometria do problema.

d E z = d E . sin ⁡ θ = d E . D d = d E . D D 2 + R 2 =   K . d q D 2 + R 2 . D D 2 + R 2

d E z = K . D . d q D 2 + R 2 3 2

Passo 6

Integrar o valor do campo elétrico projetado ao longo do anel:

E z = K . D . ∫ d q D 2 + R 2 3 2 = K . D D 2 + R 2 3 2 . ∫ d q = K . D . Q D 2 + R 2 3 2

Passo 7

Vamos chamar o campo elétrico gerado pelo anel de raio R ' de E ' . A projeção dele no eixo de simetria Z será chamada de E Z ' . Notar que o cálculo é muito parecido ao realizado no passo anterior.

Temos apenas que substituir a carga Q pela carga Q ' deste anel e substituir o raio R pelo outro raio R ' . Assim:

E z ' = K . D . Q ' D 2 + R ' 2 3 2

Passo 8

A questão informa que o campo elétrico no ponto P é nulo. Logo:

E z + E z ' = 0

Assim, temos que substituir as equações dos dois passos anteriores na igualdade acima e isolar Q ' para obter a resposta do problema:

K . D . Q ' D 2 + R ' 2 3 2 + K . D . Q D 2 + R 2 3 2 = 0 →

Q ' D 2 + R ' 2 3 2 + Q D 2 + R 2 3 2 = 0 →

Q ' D 2 + R ' 2 3 2 = - Q D 2 + R 2 3 2 →

Q ' = - Q . D 2 + R ' 2 3 2 D 2 + R 2 3 2

Q ' = - Q . ( 2 R ) 2 + 3 R 2 ( 2 R ) 2 + R 2 3 2

Resposta

Q ' = - Q . 13 5 3 2 = - 4,19 . Q

Exercício Resolvido #6

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 47-35.

A que distância do eixo de um disco de plástico uniformemente carregado de 0,600 m de raio o módulo do campo elétrico é igual à metade do módulo do campo no centro do disco?

Passo 1

Observar que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenas rosquinhas de largura d r e raio r como a indicada em verde na figura acima.

A área infinitesimal dessas rosquinhas vale a derivada da área do círculo de raio r em relação a r :

A = π r 2 → d A d r = 2 π r → d A = 2 π r d r

Passo 2

Calcular a carga infinitesimal da região verde, multiplicando a pequena área d A pela densidade superficial de campo, que é constante pois o disco está uniformemente carregado.

d q = σ d A = 2 π r σ d r

Passo 3

Note que a resultante do campo elétrico se encontra no eixo Z , devido à simetria do problema. Isso por que dois pontos do anel radialmente opostos dão campos de mesma intensidades e que somados dão um campo na direção z ^ como na figura abaixo

Então:

E R E S = E Z

Passo 4

Determinar quem é o campo infinitesimal gerado por cada pedacinho verde da figura e substituir d q na equação encontrada.

d E = K d q P M ¯ 2 = K 2 π r σ d r P M ¯ 2 = K 2 π r σ d r z 2 + r 2 2

d E = K 2 π r σ d r z 2 + r 2

Passo 5

Precisamos descobrir E Z , para isso devemos projetar o campo infinitesimal do passo anterior no eixo O z .

d E z = d E cos ⁡ α = d E z P M ¯ = d E z z 2 + r 2 = K 2 π r σ d r z 2 + r 2 z z 2 + r 2

d E z = K . 2 π r σ z d r z 2 + r 2 3 2

Passo 6

Resolvendo a integral:

E z = ∫ r = 0 r = R d E z = ∫ 0 R K 2 π r σ z d r z 2 + r 2 3 / 2

E z = 2 π σ z K ∫ 0 R r . d r z 2 + r 2 3 / 2

Agora o lance é resolver essa integral. GERALMENTE essa integral vem num formulário da sua prova, mas se não vier vamos ensinar aqui você a fazer! Pra isso pega aí aquela sua caneta/lapiseira/lápis especial e me acompanha, belê?

Passo 7

Primeiro de tudo, essa integral não sai direto! Pra isso temos que fazer uma substituição.

Olhando pra ela

∫ 0 R r d r z 2 + r 2 3 / 2

Vamos ter que simplificar esse denominador. Como em cima tem um r d r , a integral tá pedindo pra gente fazer a seguinte substituição

u = z 2 + r 2

De forma que

d u = 2 r d r → r d r = d u 2

E os limites de integração ficam

r = 0 → u = z 2 + 0 2 = z 2

r = R → u = z 2 + R 2

Então a nossa integral vai ficar

∫ 0 R r . d r z 2 + r 2 3 / 2 = ∫ z 2 R 2 + z 2 d u / 2 u 3 / 2 = 1 2 ∫ z 2 R 2 + z 2 u - 3 / 2 d u

Essa integral vai ser

∫ u - 3 / 2 d u = - 2 u - 1 / 2

Assim a nossa integral fica

1 2 ∫ z 2 R 2 + z 2 u - 3 / 2 d u = 1 2 - 2 u - 1 / 2 = - 1 u 1 / 2 z 2 z 2 + R 2 = 1 u 1 / 2 z 2 + R 2 z 2

1 2 ∫ z 2 R 2 + z 2 u - 3 / 2 d u = 1 z 2 - 1 z 2 + R 2

Finalmente

∫ 0 R r . d r z 2 + r 2 3 / 2 = 1 z - 1 z 2 + R 2

Voltando para o nosso campo

E z = 2 π σ z K 1 z - 1 z 2 + R 2

Supondo z > 0 , vamos ter z = z

E z = 2 π K σ 1 - z R 2 + z 2

Passo 8

Determinar o campo elétrico no centro do disco, que ocorre quando z = 0 :

E z = 0 = 2 π . K . σ . 1 - 0 R 2 + 0 = 2 π . K . σ

Queremos saber em que posição o campo vale a metade disso.

Passo 9

Logo:

2 π . K . σ 2 = π . K . σ = 2 π . K . σ . 1 - z R 2 + z 2 →

1 2 = 1 - z R 2 + z 2 →

z R 2 + z 2 = 1 2 →

z = R 3 = 0,600 3 = 0,346   m

Resposta

z = 0,346   m

Exercício Resolvido #7

UFRJ-P1-2010.2-D1

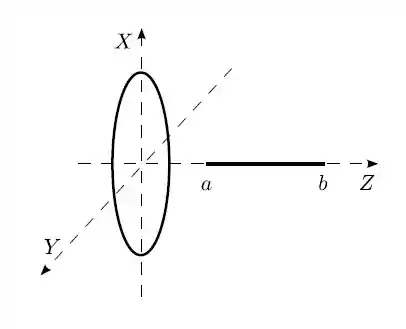
Um anel circular, muito fino, de raio R , encontra-se em repouso no plano X Y , com seu centro na origem. Tal anel possui carga total Q , uniformemente distribuída.

  1. Calcule o vetor campo elétrico (módulo, direção e sentido) devido a tal anel num ponto do eixo Z , com cota arbitrária z .
  2. Considere agora um bastão retilíneo, muito fino, em repouso, situado no eixo Z , entre z = a > 0 e z = b > a . Tal bastão também possui carga total Q , uniformemente distribuída. Calcule o vetor força elétrica sobre tal bastão devido ao anel. (Sugestão: a força sobre o bastão constitui-se da soma vetorial das forças sobre cada elemento infinitesimal do bastão carregado).

Passo 1

Pegando uma partícula infinitesimal d q podemos escrever a expressão do seu campo:

d E → = k d q r 2 r ^

Decompondo nas duas componentes:

d E → = d E x i ^ + d E y j ^ + d E z k ^

Integramos:

E → = ∫ anel   d E x x ^ + d E y y ^ + d E z z ^

Passo 2

Podemos utilizar argumentos de simetria para justificar que só existe componente em z :

∫ anel   d E x i ^ = ∫ anel   d E y j ^ = 0

Continuando:

E → = ∫ anel   d E z z ^

Encontramos a componente z por decomposição:

d E z = k d q R 2 + z 2 cos ⁡ ϕ

d E z = k d q R 2 + z 2 z R 2 + z 2

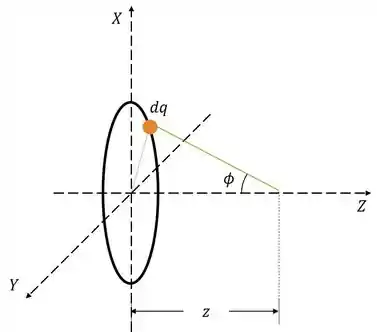
Lembrando que o triângulo é retângulo na origem dos eixos coordenados, e não onde está a carga d q .

Passo 3

Além disso, como a gente quer o campo no eixo z , que é o eixo de simetria do anel, note como o campo não depende das coordenadas x e y . O anel está no plano X Y , então podemos tirar da integral um tanto de coisas:

E → = ∫ anel   k   d q R 2 + z 2 z R 2 + z 2 z ^

E → = k R 2 + z 2 z R 2 + z 2 z ^ ∫ anel   d q

E → = k z R 2 + z 2 3 / 2 z ^ ∫ anel   d q

A integral da carga no anel dá a sua carga total:

E → = k Q z R 2 + z 2 3 / 2 z ^

Passo 4

Agora pra calcular a força é só montar a equação da força infinitesimal que o campo faz numa carga infinitesimal (Lei de Coulomb):

d F → = d q   E →

Integrando na barra toda:

F → = ∫ a b E → d q

Substituindo:

F → = ∫ a b k Q z R 2 + z 2 3 2 z ^ d q

Passo 5

Agora atenção! Trocamos o diferencial de carga pela equação da densidade da barra:

d q = λ d z

Sabemos que a distribuição de carga é uniforme, portanto isto implica numa densidade constante igual à:

λ = Q total L total = Q b - a

Que é a carga total pelo comprimento total. Logo:

d q = Q b - a d z

Integrando:

F → = ∫ a b k Q z R 2 + z 2 3 2 z ^ Q b - a z ^   d z

F → = k Q 2 b - a z ^ ∫ a b z R 2 + z 2 3 2 z ^ d z

Passo 6

Fazemos substituição simples:

v = R 2 + z 2 → d v = 2 z   d z

A indefinida fica:

I * = ∫ ( d v / 2 ) v 3 / 2

I * = 1 2 ∫ v - 3 2 d v

I * = 1 2 × - 2 × v - 1 2

I * = - 1 v

Passo 7

Logo:

F → = k Q 2 b - a z ^ - 1 R 2 + z 2 a b

F → = - k Q 2 b - a 1 R 2 + b 2 - 1 R 2 + a 2 z ^

Fica ligado de não esquecer esse sinal de menos na frente de tudo. E é só!

Resposta

a)

E → = k Q z R 2 + z 2 3 / 2 z ^

b)

F → = - k Q 2 b - a 1 R 2 + b 2 - 1 R 2 + a 2 z ^

Exercício Resolvido #8

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 46-28.

A figura abaixo mostra dois anéis concêntricos de raios R e R ' = 3,00 R , que estão no mesmo plano. O ponto P está no eixo central Z , a uma distância D = 2,00 R do centro dos anéis. O anel menor possui carga uniforme distribuída Q . Em termos de Q , qual deve ser a carga uniformemente distrubuída no anel maior para que o campo elétrico no ponto P seja nulo?

Passo 1

Notar a simetria do problema: o campo elétrico resultante E R está na direção Z , então, precisamos descobrir apenas qual é a componente desse campo nesta direção.

E R = E Z

Passo 2

Calcular o campo elétrico que um pedaço do anel, com carga infinitesimal d q , exerce no ponto P :

d E = K . d q d 2

Onde d é a distância entre um ponto do anel e o ponto P como podemos ver na figura abaixo:

Passo 3

Calcular, pela geometria do problema, o valor de d 2 em função de R e de D :

d 2 = D 2 + R 2

Passo 4

Substituir na equação do segundo passo:

d E = K . d q D 2 + R 2

Passo 5

Olhar novamente o triângulo representado acima. Calcular a projeção do campo elétrico no eixo de simetria pela geometria do problema.

d E z = d E . sin ⁡ θ = d E . D d = d E . D D 2 + R 2 =   K . d q D 2 + R 2 . D D 2 + R 2

d E z = K . D . d q D 2 + R 2 3 2

Passo 6

Integrar o valor do campo elétrico projetado ao longo do anel:

E z = K . D . ∫ d q D 2 + R 2 3 2 = K . D D 2 + R 2 3 2 . ∫ d q = K . D . Q D 2 + R 2 3 2

Passo 7

Vamos chamar o campo elétrico gerado pelo anel de raio R ' de E ' . A projeção dele no eixo de simetria Z será chamada de E Z ' . Notar que o cálculo é muito parecido ao realizado no passo anterior.

Temos apenas que substituir a carga Q pela carga Q ' deste anel e substituir o raio R pelo outro raio R ' . Assim:

E z ' = K . D . Q ' D 2 + R ' 2 3 2

Passo 8

A questão informa que o campo elétrico no ponto P é nulo. Logo:

E z + E z ' = 0

Assim, temos que substituir as equações dos dois passos anteriores na igualdade acima e isolar Q ' para obter a resposta do problema:

K . D . Q ' D 2 + R ' 2 3 2 + K . D . Q D 2 + R 2 3 2 = 0 →

Q ' D 2 + R ' 2 3 2 + Q D 2 + R 2 3 2 = 0 →

Q ' D 2 + R ' 2 3 2 = - Q D 2 + R 2 3 2 →

Q ' = - Q . D 2 + R ' 2 3 2 D 2 + R 2 3 2

Q ' = - Q . ( 2 R ) 2 + 3 R 2 ( 2 R ) 2 + R 2 3 2

Resposta

Q ' = - Q . 13 5 3 2 = - 4,19 . Q

Exercício Resolvido #9

UNICAMP-P1-2007.2-2

Uma barra isolada, de comprimento L , tem uma carga + Q distribuída uniformemente ao longo de sua extensão, conforme a figura.

a ) Determine o vetor campo elétrico no ponto P , situado a uma distância a da extremidade direita da barra;

b ) Suponha que uma outra carga isolada puntiforme + Q seja colocada num outro ponto distante 3 a da extremidade direita da barra. Determine o vetor campo elétrico no ponto P devido apenas à carga isolada;

c ) Determine, agora, o vetor campo elétrico total no ponto P ;

Passo 1

a ) Determine o vetor campo elétrico no ponto P , situado a uma distância a da extremidade direita da barra;

Beleza!

Pra resolver esse tipo de problema, vamos começar pegando, da barra, uma pedaço infinitesimal de carga d q e ver o campo elétrico produzido por ela.

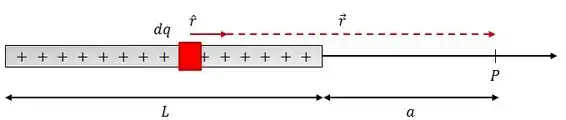
O campo elétrico gerado pelo elemento de carga d q é dado por:

d E → = d q 4 π ϵ 0 r 2   r ^

Passo 2

Antes de voltarmos pra fórmula, repara que a carga infinitesimal d q pode ser escrita em função da densidade linear de carga λ .

d q = λ d r

Agora sim!

Passo 3

d E → = λ d r 4 π ϵ 0 r 2   r ^

Agora é só integrar esse cara, onde:

a ≤ r ≤ a + L

Logo:

E → = λ 4 π ϵ 0   ∫ a a + L d r r 2   r ^

E → = λ 4 π ϵ 0   - 1 r a a + L r ^

E → = λ 4 π ϵ 0   1 a - 1 a + L r ^

E → = λ 4 π ϵ 0 L a a + L r ^

E → = λ L 4 π ϵ 0 a ( a + L ) r ^

Como λ = Q L → Q = λ L , podemos substituir de volta. Além disso, r ^ = x ^ , logo:

E → = Q 4 π ϵ 0 a ( a + L ) x ^

Ah! Ao invés de r , você poderia ter usado x logo de cara também... não tem problema. Só procura desenhar o vetor pra especificar o jeito como você está usando ele.

Passo 4

b ) Suponha que uma outra carga isolada puntiforme + Q seja colocada num outro ponto distante 3 a da extremidade direita da barra. Determine o vetor campo elétrico no ponto P devido apenas à carga isolada;

Opa! Agora ficou tranquilo, só alegria!

O campo elétrico gerado por uma carga pontual é dado por:

E → = 1 4 π ϵ 0 Q r 2 r ^

Como a carga + Q é colocada a uma distância 3 a da extremidade direita da barra, ela vai estar a uma distância 2 a do ponto P , como mostra a figura do enunciado.

Além disso, como a carga é positiva e está à direita do ponto P :

r ^ = - x ^

Portanto, substituindo na equação do campo elétrico:

E → = - 1 4 π ϵ 0 Q 2 a 2 x ^

E → = - 1 4 π ϵ 0 Q 4 a 2 x ^

E → = - Q 16 π ϵ 0 a 2 x ^

Passo 5

c ) Determine, agora, o vetor campo elétrico total no ponto P ;

Como o campo elétrico é uma grandeza vetorial, o campo elétrico total vai ser a soma vetorial dos campos que calculamos na letra a e na letra b :

E → R = E → a + E → b

E → R = Q 4 π ϵ 0 a ( a + L ) - Q 16 π ϵ 0 a 2 x ^

E → R = Q 4 π ϵ 0 a 1 a + L - 1 4 a x ^

Peraí! Só isso?!

Sim, só isso! ;)

Resposta

a )

E → = Q 4 π ϵ 0 a ( a + L ) x ^

b )

E → = - Q 16 π ϵ 0 a 2 x ^

c )

E → R = Q 4 π ϵ 0 a 1 a + L - 1 4 a x ^

Exercício Resolvido #10

UFRJ-P1-2010.2-D1

Um anel circular, muito fino, de raio R , encontra-se em repouso no plano X Y , com seu centro na origem. Tal anel possui carga total Q , uniformemente distribuída.

  1. Calcule o vetor campo elétrico (módulo, direção e sentido) devido a tal anel num ponto do eixo Z , com cota arbitrária z .
  2. Considere agora um bastão retilíneo, muito fino, em repouso, situado no eixo Z , entre z = a > 0 e z = b > a . Tal bastão também possui carga total Q , uniformemente distribuída. Calcule o vetor força elétrica sobre tal bastão devido ao anel. (Sugestão: a força sobre o bastão constitui-se da soma vetorial das forças sobre cada elemento infinitesimal do bastão carregado).

Passo 1

Pegando uma partícula infinitesimal d q podemos escrever a expressão do seu campo:

d E → = k d q r 2 r ^

Decompondo nas duas componentes:

d E → = d E x i ^ + d E y j ^ + d E z k ^

Integramos:

E → = ∫ anel   d E x x ^ + d E y y ^ + d E z z ^

Passo 2

Podemos utilizar argumentos de simetria para justificar que só existe componente em z :

∫ anel   d E x i ^ = ∫ anel   d E y j ^ = 0

Continuando:

E → = ∫ anel   d E z z ^

Encontramos a componente z por decomposição:

d E z = k d q R 2 + z 2 cos ⁡ ϕ

d E z = k d q R 2 + z 2 z R 2 + z 2

Lembrando que o triângulo é retângulo na origem dos eixos coordenados, e não onde está a carga d q .

Passo 3

Além disso, como a gente quer o campo no eixo z , que é o eixo de simetria do anel, note como o campo não depende das coordenadas x e y . O anel está no plano X Y , então podemos tirar da integral um tanto de coisas:

E → = ∫ anel   k   d q R 2 + z 2 z R 2 + z 2 z ^

E → = k R 2 + z 2 z R 2 + z 2 z ^ ∫ anel   d q

E → = k z R 2 + z 2 3 / 2 z ^ ∫ anel   d q

A integral da carga no anel dá a sua carga total:

E → = k Q z R 2 + z 2 3 / 2 z ^

Passo 4

Agora pra calcular a força é só montar a equação da força infinitesimal que o campo faz numa carga infinitesimal (Lei de Coulomb):

d F → = d q   E →

Integrando na barra toda:

F → = ∫ a b E → d q

Substituindo:

F → = ∫ a b k Q z R 2 + z 2 3 2 z ^ d q

Passo 5

Agora atenção! Trocamos o diferencial de carga pela equação da densidade da barra:

d q = λ d z

Sabemos que a distribuição de carga é uniforme, portanto isto implica numa densidade constante igual à:

λ = Q total L total = Q b - a

Que é a carga total pelo comprimento total. Logo:

d q = Q b - a d z

Integrando:

F → = ∫ a b k Q z R 2 + z 2 3 2 z ^ Q b - a z ^   d z

F → = k Q 2 b - a z ^ ∫ a b z R 2 + z 2 3 2 z ^ d z

Passo 6

Fazemos substituição simples:

v = R 2 + z 2 → d v = 2 z   d z

A indefinida fica:

I * = ∫ ( d v / 2 ) v 3 / 2

I * = 1 2 ∫ v - 3 2 d v

I * = 1 2 × - 2 × v - 1 2

I * = - 1 v

Passo 7

Logo:

F → = k Q 2 b - a z ^ - 1 R 2 + z 2 a b

F → = - k Q 2 b - a 1 R 2 + b 2 - 1 R 2 + a 2 z ^

Fica ligado de não esquecer esse sinal de menos na frente de tudo. E é só!

Resposta

a)

E → = k Q z R 2 + z 2 3 / 2 z ^

b)

F → = - k Q 2 b - a 1 R 2 + b 2 - 1 R 2 + a 2 z ^

Exercício Resolvido #11

UNICAMP-P1-2007.2-2

Uma barra isolada, de comprimento L , tem uma carga + Q distribuída uniformemente ao longo de sua extensão, conforme a figura.

a ) Determine o vetor campo elétrico no ponto P , situado a uma distância a da extremidade direita da barra;

b ) Suponha que uma outra carga isolada puntiforme + Q seja colocada num outro ponto distante 3 a da extremidade direita da barra. Determine o vetor campo elétrico no ponto P devido apenas à carga isolada;

c ) Determine, agora, o vetor campo elétrico total no ponto P ;

Passo 1

a ) Determine o vetor campo elétrico no ponto P , situado a uma distância a da extremidade direita da barra;

Beleza!

Pra resolver esse tipo de problema, vamos começar pegando, da barra, uma pedaço infinitesimal de carga d q e ver o campo elétrico produzido por ela.

O campo elétrico gerado pelo elemento de carga d q é dado por:

d E → = d q 4 π ϵ 0 r 2   r ^

Passo 2

Antes de voltarmos pra fórmula, repara que a carga infinitesimal d q pode ser escrita em função da densidade linear de carga λ .

d q = λ d r

Agora sim!

Passo 3

d E → = λ d r 4 π ϵ 0 r 2   r ^

Agora é só integrar esse cara, onde:

a ≤ r ≤ a + L

Logo:

E → = λ 4 π ϵ 0   ∫ a a + L d r r 2   r ^

E → = λ 4 π ϵ 0   - 1 r a a + L r ^

E → = λ 4 π ϵ 0   1 a - 1 a + L r ^

E → = λ 4 π ϵ 0 L a a + L r ^

E → = λ L 4 π ϵ 0 a ( a + L ) r ^

Como λ = Q L → Q = λ L , podemos substituir de volta. Além disso, r ^ = x ^ , logo:

E → = Q 4 π ϵ 0 a ( a + L ) x ^

Ah! Ao invés de r , você poderia ter usado x logo de cara também... não tem problema. Só procura desenhar o vetor pra especificar o jeito como você está usando ele.

Passo 4

b ) Suponha que uma outra carga isolada puntiforme + Q seja colocada num outro ponto distante 3 a da extremidade direita da barra. Determine o vetor campo elétrico no ponto P devido apenas à carga isolada;

Opa! Agora ficou tranquilo, só alegria!

O campo elétrico gerado por uma carga pontual é dado por:

E → = 1 4 π ϵ 0 Q r 2 r ^

Como a carga + Q é colocada a uma distância 3 a da extremidade direita da barra, ela vai estar a uma distância 2 a do ponto P , como mostra a figura do enunciado.

Além disso, como a carga é positiva e está à direita do ponto P :

r ^ = - x ^

Portanto, substituindo na equação do campo elétrico:

E → = - 1 4 π ϵ 0 Q 2 a 2 x ^

E → = - 1 4 π ϵ 0 Q 4 a 2 x ^

E → = - Q 16 π ϵ 0 a 2 x ^

Passo 5

c ) Determine, agora, o vetor campo elétrico total no ponto P ;

Como o campo elétrico é uma grandeza vetorial, o campo elétrico total vai ser a soma vetorial dos campos que calculamos na letra a e na letra b :

E → R = E → a + E → b

E → R = Q 4 π ϵ 0 a ( a + L ) - Q 16 π ϵ 0 a 2 x ^

E → R = Q 4 π ϵ 0 a 1 a + L - 1 4 a x ^

Peraí! Só isso?!

Sim, só isso! ;)

Resposta

a )

E → = Q 4 π ϵ 0 a ( a + L ) x ^

b )

E → = - Q 16 π ϵ 0 a 2 x ^

c )

E → R = Q 4 π ϵ 0 a 1 a + L - 1 4 a x ^

Exercício Resolvido #12

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 47-37.

Um engenheiro foi encarregado de projetar um dispositivo no qual um disco uniformemente carregado de raio R produz em um ponto P sobre o eixo do disco a uma distância 2,00 . R do plano do disco. Para economizar material decidiu-se substituir o disco por um anel com o mesmo raio externo R e um raio interno R 2 . O anel tem a mesma densidade superficial de cargas que o disco original. Qual é a razão entre o novo campo no ponto P e o campo antigo?

Passo 1

Observe que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenos anéizinhos de largura d r e raio r como a indicada em verde na figura abaixo.

A área desse anelzinho vai ser o seu comprimento vezes a sua espessura d r

d A = 2 π . r . d r

Passo 2

A carga infinitesimal da região verde, é dada pelo produto da pequena área d A pela densidade superficial de carga, que é constante pois o disco está uniformemente carregado.

d q = σ . d A = 2 π . r . σ . d r

Passo 3

Essa distribuição de carga tem uma simetria cilindrica. Isso significa se pegarmos dois pedaços do anel diametralmente opostos (como na figura) e somarmos o campo produzido por cada um deles, o campo resultante vai estar na direção z ^

Então o nosso campo é da forma

E → R = E R z ^

Lembrando que isso tem que tá bem justificadinho na sua prova hein! Se falar que é assim só por causa da simetria dá ruim :/

Passo 4

Agora temos que montar a expressão pro campo infinitesimal do anel. Como todos os pontos do anel estão a mesma distância do ponto que queremos calcular o campo, vamos ter então

d E → a n e l = K d q ρ 2 z ^

Onde ρ = r 2 + z 2 .

Mas ainda falta uma coisa! Cada infinitésimo produz um campo inclinado em relação ao eixo z e quando somamos todos os pedaços do anel, ficamos só com a componente na direção z . Pela figura abaixo a componenente z é dada por

d E z = d E c o s ( α )

E então

d E → a n e l = K d q ρ 2 cos ⁡ α z ^

Pela figura temos que

cos ⁡ α = z ρ = z z 2 + r 2

Assim

d E → a n e l = K d q ρ 2 z z 2 + r 2 z ^

Subsitituindo ρ e d q = 2 π r σ d r

d E → a n e l = K 2 π r σ d r ( z 2 + r 2 ) z z 2 + r 2 z ^

Passo 5

Resolvendo a integral no caso (A):

E z ( A ) = ∫ 0 R d E z = ∫ 0 R K . 2 π . r . σ . z . d r z 2 + r 2 3 / 2

= 2 π . σ . z . K . ∫ 0 R r . d r z 2 + r 2 3 2

E z ( A ) = 2 π . K . σ . 1 - z R 2 + z 2

Os detalhes de como calcular esta integral estão demonstrados na teoria.

Passo 6

Resolver a integral no segundo caso (B), que é completamente parecido. Nessa situação, vamos apenas alterar os limites de integração.

E z ( B ) = ∫ R 2 R d E z = K . σ . 2 π - c o s ⁡ ( θ ) r = R 2 r = R

O limite inferior se altera, quando r = R 2 devemos calcular o novo cosseno do ângulo α :

z R 2 2 + z 2

Assim, o valor que encontramos é:

K . σ . 2 π - c o s ⁡ ( α ) r = R 2 r = R = E z ( B ) = K . σ . 2 π - z r 2 + z 2 r = R 2 r = R

= 2 π . K . σ . z R 2 2 + z 2 - z R 2 + z 2

Passo 7

Queremos a razão:

E z B E z A = 2 π . K . σ . z R 2 2 + z 2 - z R 2 + z 2 2 π . K . σ . 1 - z R 2 + z 2

E z B E z A = z R 2 2 + z 2 - z R 2 + z 2 1 - z R 2 + z 2

Substituindo z = 2 . R :

E z B E z A = 2 . R R 2 2 + ( 2 . R ) 2 - 2 . R R 2 + ( 2 . R ) 2 1 - z R 2 + ( 2 . R ) 2

Logo:

E z B E z A = 2 1 4 + 4 - 2 1 + 4 1 - 2 1 + 4 = 2 17 4 - 2 5 1 - 2 5

= 2.2 17 - 2 5 1 - 2 5 = 4 . 5 - 2 . 17 17 . ( 5 - 2 ) ≈ 0,72

Resposta

E z B E z A ≈ 0,72

Exercício Resolvido #13

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 48-52.

Um elétron e é liberado a partir do repouso no eixo central de um disco uniformemente carregado de raio R . A densidade superficial de cargas do disco é 4 μ C m 2 . Determine o módulo da aceleração inicial do elétron se ele for liberado a uma distância do centro do disco de:

(a) z = R

(b)   z = R 100

(c)   z = R 1000

(d) Por que o módulo da aceleração quase não varia com a distância entre a carga e o disco?

Dado: Razão carga massa do elétron:

e m e = 1,759.10 11 C K g  

Passo 1

Temos a seguinte situação

Observe que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenas rosquinhas de largura d r e raio r como a indicada em verde na figura acima.

A área infinitesimal dessas rosquinhas vale a derivada da área do círculo de raio r em relação a r :

A = π . r 2 → d A d r = 2 π . r → d A = 2 π . r . d r

Passo 2

Vamos calcular a carga infinitesimal da região verde, multiplicando a pequena área d A pela densidade superficial de campo, que é constante pois o disco está uniformemente carregado.

d q = σ . d A = 2 π . r . σ . d r

Passo 3

Notar que o campo elétrico resultante E R se encontra no eixo Z , devido à simetria do problema. Então:

E R = E Z

Passo 4

Temos que determinar quem é o campo infinitesimal gerado por cada pedacinho do disco carregado e substituir d q na equação encontrada.

Todos os pedacinhos d q do disco estão a uma distância z 2 + r 2 do nosso ponto! Outro ponto importante é que devido a simetria o campo tem que apontar na direção z ^ . Para pegarmos essa componente basta multiplicar por s e n ( θ ) que tá mostrado na figura acima, beleza?

Então temos

d E Z = K . d q z 2 + r 2 s e n θ

Pela figura

s e n θ = z z 2 + r 2

E já vimos que

d q = 2 π . r . σ . d r

Assim

d E Z = K . 2 π . r . σ . d r z 2 + r 2 z z 2 + r 2

d E Z = K . 2 π . r . σ . z . d r z 2 + r 2 3 / 2

Passo 5

Agora basta integrar!

E z = ∫ x = 0 x = R d E z = ∫ r = 0 r = R K . 2 π . r . σ . z . d r z 2 + r 2 3 2

E z = 2 π . σ . z . K . ∫ r = 0 r = R r . d r z 2 + r 2 3 2

Pra fazer essa integral é só fazer a substituição u = z 2 + r 2 → d u = 2 z d z !

O resultado vai ser:

E z = 2 π . K . σ . 1 - z R 2 + z 2

Passo 6

Podemos a partir do campo determinar a força, que é igual ao produto da massa do elétron m e pela aceleração que queremos determinar:

E . e = a . m e = F e → a = E . e m e

Logo:

a = 2 π . K . σ . e m e . 1 - z R 2 + z 2

a = 2 . π . 9.10 9 . 4.10 - 6 . 1,759.10 11 . 1 - z R 2 + z 2

a ≈ 4.10 16 . 1 - z R 2 + z 2

Passo 7

Substituir os valores sugeridos no problema:

(a) Se z = R → a = 4.10 16 . 1 - z R 2 + z 2 = 4.10 16 . 1 - R R 2 + R 2 = 4.10 16 . 1 - 1 2

a ≈ 1,17.10 16 m / s 2

(b) Se z = R 100 → a = 4.10 16 . 1 - z R 2 + z 2 = 4.10 16 . 1 - R R 2 + R 2 100 2 =

a = 4.10 16 . 1 - 1 1,0001

a ≈ 3,95.10 16 m / s 2

(c) Se z = R 1000 → a = 4.10 16 . 1 - z R 2 + z 2 = 4.10 16 . 1 - R R 2 + R 2 1000 2 =

a = 4.10 16 . 1 - 1 1,000001

a ≈ 3,97.10 16 m / s 2

Passo 8

O módulo da aceleração quase não varia para menores distâncias entre a carga e o disco porque a resultante da força produzida pelas cargas próximas da borda do disco diminuir com a redução da distância entre o elétron e o centro do disco.

Quando a distância z do elétron é muito menor que o raio do disco, o elétron “vê” esse disco como um plano infinito! Lembra como era o campo de um plano infinito? Ele não depende da distância da carga até o plano! A mesma coisa acontece aqui desde que a distância z seja muito menor do que o raio do disco!

Outra forma mais matemática de ver isso é:

a = 4.10 16 . 1 - z R 2 + z 2 = 4.10 16 . 1 - z R 2 z 2 R 2 + 1

a = 4.10 16 . 1 - z R z 2 R 2 + 1

a = 4.10 16 . 1 - z R 1 + z 2 R 2 1 / 2

No limite z ≪ R , a gente pode fazer a razão z / R tender a zero já que essa razão é um número muito pequeninho! Então nesse limite

a ≈ 4.10 16 . 1 - 0

a ≈ 4.10 16   m / s 2

Resposta

(a) Se z = R → a ≈ 1,17.10 16

(b) Se z = R 100 → a ≈ 3,95.10 16

(c) Se z = R 1000 → a ≈ 3,97.10 16

(d) O módulo da aceleração quase não varia para menores distâncias entre a carga e o disco porque a resultante da força produzida pelas cargas próximas da borda do disco diminuir com a redução da distância entre o elétron e o centro do disco.

Isso ocorre porque nessas posições essas forças quase se cancelam e apenas as cargas próximas ao centro do disco exercem influência no elétron.

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri