Lei de Gauss em Condutores
Produzido por Bruno SoaresTeoria
Introdução
Já ouviu falar em superfícies condutoras? É comum em dias de chuva evitarmos levar objetos de metal já que muitos dizem que o metal atrai cargas pra si, será que isso é verdade?
Objetos metálicos são sim bons condutores de energia, pois as cargas conseguem se mover livremente. Por isso que devemos evitar tocar objetos metálicos nas trovoadas, por que se ele estiver energizado ele pode passar os elétrons até você e você leva o choque.
Como as cargas podem se mover livremente, elas começam a se afastar por causa da lei de coulomb, que diz que cargas de mesmo sinal se repelem. Nesse processo as cargas vão para a superfície do condutor, pois nesse ponto é onde elas conseguem se afastar ao máximo umas das outras e por isso não haverá carga no interior do condutor.

Um condutor carregado vai ter também uma grande densidade superficial de cargas, ou seja, muita carga distribuída pela sua área superficial, e podemos calculá-la:
Mas e aí, se esse cara tem cargas na superfície, deve ter algum campo elétrico nele e como será que a gente calcula?

Lei de Gauss e Condutores
Vamos considerar uma esfera maciça com raio , carregada positivamente com . Como não há cargas no seu interior, pela Lei de Gauss, vemos que o campo no interior do condutor será zero:

Já na superfície do condutor, haverá a presença de cargas que produzem campo elétrico e poderemos calculá-lo através da lei de Gauss.
E esse campo elétrico é perpendicular à superfície, no mesmo sentido do vetor .
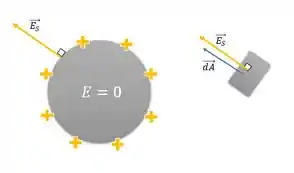
Então se liga, se os vetores são paralelos o ângulo entre eles é zero e podemos reescrever aquela integral do fluxo desse jeito aqui:
Onde a área é a área da superfície Gaussiana e como queremos calcular o campo elétrico na superfície do nosso condutor, a nossa Gaussiana será uma superfície esférica com o mesmo raio que o condutor e a área será:
Porém, supondo que a densidade superficial de cargas sobre o corpo metálico é constante, temos que:
Assim, podemos encontrar para o campo na superfície externa, usando a equação.
Portanto substituindo a carga ( e o raio da esfera () teremos:
Substituindo a constante de permissividade elétrica temos:
Campo Elétrico em Placas Infinitas
Caso os condutores se tratem de placas, para calcular o campo elétrico em sua superfície, deveremos fazer uma média entre o campo externo e o campo interno.
E como todo condutor, tem o campo elétrico no seu interior igual à zero, teremos então que o campo na superfície da placa será:
No caso de placas infinitas, o campo elétrico no seu exterior é constante e é dado pela Lei de Gauss como sendo:
Então o campo na superfície, vai ser:
Isso ocorre porque existe uma transição entre o campo igual a zero e o campo igual à densidade dividida por , o que nos faz considerar o valor médio quando estamos exatamente na situação limite.
Se liga, que esse caso da média não é válido para condutores esféricos ou cilíndricos!

Show de bola? Vamos exercitar, então? Partiu!