Lei de Gauss simetria
Produzido por Bruno SoaresTeoria
Fala aí, nós somos o Responde Aí, a solução para a sua faculdade fluir mais leve e não ter todo aquele sofrimento com as matérias hahaha. Estamos aqui hoje para falar um pouco sobre as simetrias dentro da Lei de Gauss, show?
A Lei de Gauss já nos disse que o fluxo do campo em uma superfície fechada ao redor de uma região é igual à razão entre a carga interna e a constante
Essa lei é válida para qualquer situação, sendo o campo elétrico uniforme ou não, e para qualquer superfície fechada chamada de gaussiana. Entretanto, para que ela possa ser útil e seja possível calcular o campo elétrico a partir dela é necessário que se busque simetrias para que a equação possa ser simplificada e seja possível encontrar o campo através de contas manuais.
Para encontrar essas simetrias, vamos seguir duas regrinhas:
- O campo elétrico deve ser ortogonal a todos os pontos da superfície gaussiana;
Se o campo elétrico é ortogonal a todos os pontos da superfície gaussiana, nós temos que o vetor
- O módulo do campo elétrico deve ser igual em todos os pontos da superfície gaussiana
Se o módulo do campo elétrico é igual em todos os pontos da gaussiana, nós podemos tirá-lo da integral:
Assim, ficamos apenas com a integral de
E assim podemos isolar
Ficou muito muito mais simples, não é mesmo?
Mas a grande questão é: Como vamos conseguir que essas duas regrinhas sejam satisfeitas para facilitar a nossa vida? O grande segredo está na escolha da superfície gaussiana. Vamos escolher a gaussiana sempre parecida com o objeto que está carregado e gerando o campo, porque desse modo a gente se utiliza da simetria do próprio objeto. Por exemplo, se temos uma esfera carregada, escolheremos uma superfície gaussiana esférica, se temos um cilindro carregado gerando campo, vamos escolher uma superfície gaussiana cilíndrica, sacou?
Pensando nisso, existem três simetrias:
- Simetria Esférica;
- Simetria Cilíndrica, e;
- Simetria Planar
Vamos falar rapidamente de cada uma delas.
Simetria Esférica
Essa simetria é utilizada quando temos uma carga puntiforme ou uma distribuição esférica de cargas gerando o campo elétrico. Nela escolhemos uma superfície gaussiana esférica e isso faz com que as nossas regrinhas sejam satisfeitas:
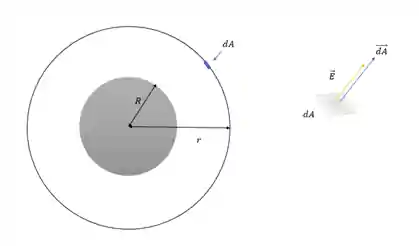
Assim, para calcularmos o módulo de campo elétrico, precisamos apenas saber a carga total que está no interior da gaussiana e a área da superfície esférica, que nós sabemos calcular porque é uma esfera:
Simetria Cilíndrica
Essa é utilizada quando temos fios de uma dimensão ou cilindros infinitos gerando o campo elétrico e nós usamos uma superfície gaussiana cilíndrica ao redor do objeto carregado para que, novamente, as nossas regrinhas sejam satisfeitas:
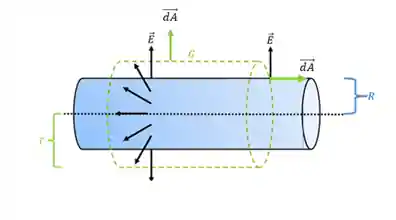
E novamente, precisaremos apenas calcular a área da superfície gaussiana, que será a área lateral do cilindro:
Simetria Planar
Essa simetria é utilizada quando temos um plano infinito carregado gerando o campo elétrico e usamos uma superfície gaussiana no formato de um paralelepípedo. Assim, as duas regrinhas são atendidas:
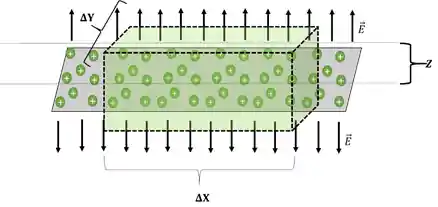
Nesse caso, a área que teremos que utilizar é apenas a área superior e inferior do paralelepípedo, porque apenas por essas áreas tem fluxo de campo elétrico. A área inferior e superior do nosso paralelepípedo são iguais e valem
Viu como essas simetrias facilitam demais demais a nossa vida? Então, guarda elas no coração porque com toda certeza você vai precisar delas na prova, estamos combinados?
Vídeo
Você pode ver esse conteúdo em vídeo também. O vídeo é bem rapidinho e bem esclarecedor assim como todos os vídeos do Responde Aí. Dá uma conferida aqui 👇🏾