Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Lei de Gauss

Ver Todos os Exercícios

Teoria

A lei de Gauss nos da a relação entre o fluxo do campo elétrico e carga elétrica que existe dentro de um volume limitado, chamado superfície gaussiana.

O que diz a lei de Gauss?

A lei de Gauss diz que:

“O fluxo do campo elétrico através de uma superfície fechada hipotética (superfície gaussiana) é proporcional à carga líquida dentro dela”.

A Fórmula da lei de Gauss tem essa carinha aqui:

Onde:

  • é o fluxo de campo elétrico sobre uma superfície FECHADA (gaussiana), expresso em ;
  • é a carga que está envolvida pela gaussiana, a carga que está interna a essa superfície, expressa em ;
  • é a constante de permissividade do vácuo, que vale:

-Hãam?! 😖

Calma… para entender o significado da lei de Gauss na prática, primeiro você precisa entender algumas definições, como superfície gaussiana e luxo do campo elétrico.

A gente vai explicar tudinho passo a passo e você vai sair daqui sabendo tudo o que você precisa pra arrasar na prova de Física! Então bora começar com esse vídeozinho super completo sobre a lei de Gauss?! 👇 🧡

Lei de Gauss: Conceitos Importantes

Antes de qualquer coisa, vamos relembrar o conceito de linhas de campo elétrico.

Devemos ter em mente que cargas elétricas positivas "cospem" linhas de campo elétrico, enquanto cargas negativas puxam linhas de campo elétrico pra elas. Como na imagem:

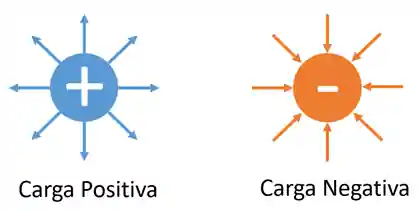
Linhas de campo de uma carga positiva e negativa
Linhas de campo de uma carga positiva e negativa

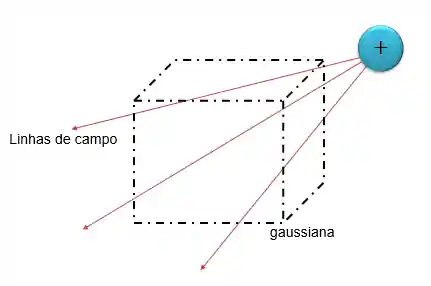
Agora, vamos imaginar que pegamos uma carga positiva e colocamos ela dentro de uma caixa, desse jeitinho aqui:

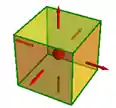
Superfície Gaussiana
Superfície Gaussiana

Concorda comigo que podemos imaginar que as linhas de campo elétrico produzidas pela carga positiva estão atravessando as faces da nossa caixa? E isso é o que chamamos de fluxo elétrico, a quantidade de campo elétrico que atravessa uma superfície por unidade de área.

A Lei de Gauss fala exatamente sobre esse exemplo, ela relaciona o fluxo de campo elétrico sobre uma superfície fechada, chamada de gaussiana, com a carga total que é envolvida por essa superfície, chamada de carga interna.

A superfície gaussiana é uma superfície fechada tridimensional e imaginária que vamos usar aqui, como uma espécie de volume de controle!

Como usar a Lei de Gauss?

Pra conseguirmos usar a lei de Gauss nos exercícios sem problemas, precisamos ter em mente algumas implicações importantes dessa lei.

1º) O fluxo de campo elétrico tem o mesmo sinal da carga interna

Isso porque carga positiva cospe o campo elétrico e o fluxo resultante é para fora da superfície, como podemos ver na imagem anterior, e tem o sinal positivo, enquanto carga negativa puxa o campo elétrico, fazendo com que o fluxo seja para dentro da gaussiana, assumindo um sinal negativo. De forma geral:

éã
éã
éã

2°) O formato da superfície gaussiana não altera o fluxo de campo elétrico.

A lei de Gauss relaciona o fluxo de campo elétrico sobre uma superfície fechada com a carga que está no interior da superfície, então não importa qual o formato da minha superfície gaussiana, se a carga no interior é a mesma, o fluxo elétrico será o mesmo:

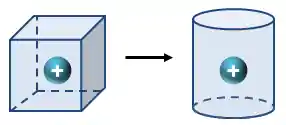
Formato da superfície gaussiana
Formato da superfície gaussiana

Ou seja:

3°) Se houver mais de uma carga envolvida pela a gaussiana, a carga interna será a soma de todas as cargas que estão no interior da gaussiana

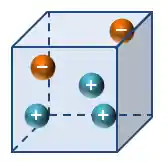
Gaussiana: Cargas internas
Gaussiana: Cargas internas

Nessa imagem temos cargas no inteiro da superfície gaussiana, então a carga interna será:

4°) Cargas fora da gaussiana não contribuem para o fluxo elétrico.

Isso ocorre porque quando a carga está fora da gaussiana a quantidade de campo produzida por ela que entra na gaussiana é igual a quantidade de campo que sai da gaussiana e assim a contribuição do campo produzido por essa carga no fluxo é nula.

Cargas fora da superfície gaussiana
Cargas fora da superfície gaussiana

E essa é a Lei de Gauss e suas aplicações. Agora vamos praticar com exercícios?

Lei de Gauss: Conceitos Importantes

Como usar a Lei de Gauss?

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-P1-2014.2-ME04

Seja um cubo isolante e uniformemente carregado, isolado de todos os outros corpos.

Dentre as afirmações

I A lei de Gauss só se aplica a esse problema se escolhermos superfícies gaussianas cúbicas, haja vista a simetria do sistema,

I I A lei de Gauss deixa de ser aplicável a esse problema se escolhermos superfícies gaussianas que interceptam o cubo carregado,

I I I A lei de Gauss simplesmente não se aplica a esse problema;

qual(is) é(são) verdadeira(s)?

a Somente a I .

b Somente a I I .

c Somente a I I I .

d Somente a I e a I I .

e Somente a I e a I I I .

f Somente a I I e a I I I .

g Todas estão corretas.

h Nenhuma está correta.

Passo 1

Vamos analisar cada afirmativa.

I A lei de Gauss só se aplica a esse problema se escolhermos superfícies gaussianas cúbicas, haja vista a simetria do sistema

De acordo com a lei de Gauss, independente do formato da gaussiana, o fluxo elétrico através da superfície é sempre o mesmo. Logo, a superfície gaussiana pode ter qualquer formato (esférica, cilíndrica, cúbica, etc.), desde que englobe todas as cargas do sistema.

A afirmativa é falsa.

Passo 2

I I A lei de Gauss deixa de ser aplicável a esse problema se escolhermos superfícies gaussianas que interceptam o cubo carregado

A lei de Gauss contínua sendo aplicável se ela cortar o cubo! Se ela cortar o cubo na metade, então na lei de Gauss temos que usar metade da carga desse cubo. Ela sempre é aplicável, mas isso não significa que ela é conveniente pois as contas ficariam muito difíceis!

A afirmativa é falsa.

Passo 3

I I I A lei de Gauss simplesmente não se aplica a esse problema

A lei de Gauss se aplica a esse problema sim! O problema é escolher uma superfície que faça as contas serem fáceis, mas a lei de Gauss se aplica com certeza.

A afirmativa é falsa.

A resposta certa é a letra h .

Resposta

h Nenhuma está correta.

Exercício Resolvido #2

UFRJ-P1-2010.2-ME10

Considere os seguintes sistemas carregados:

  1. Fio retilíneo, fino, finito, uniforme;
  2. Fio retilíneo, fino, finito, não uniforme;
  3. Fio retilíneo, fino, infinito, não uniforme;
  4. Anel circular, fino, uniforme;
  5. Bola (esférica), sólida, com densidade de carga variando só com a distância até o centro.

Qual a opção que indica, desses sistemas, aquele(s) para o(s) qual(is) pode-se aplicar a lei de Gauss a fim de deduzir uma expressão analítica explícita para o campo elétrico resultante?

  1. IV
  2. V
  3. I, IV
  4. I, V
  5. IV, V
  6. I, IV, V

Passo 1

Para podermos aplicar a Lei de Gauss de maneira conveniente, precisamos escolher uma superfície gaussiana por onde o campo elétrico é constante!

Para isso acontecer é necessário que tenhamos alguma simetria, como a esférica ou cilíndrica.

Passo 2

Um fio finito não possui campo de simetria cilíndrica, como alguns podem imaginar. É só olhar pra essa figura aqui

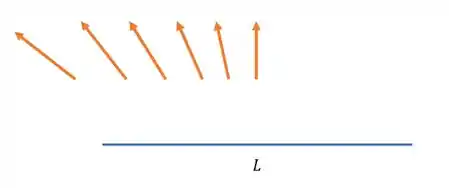
O campo logo acima do meio desse fio carregado de comprimento L é vertical, mas conforme vamos andando pra esquerda ele começa a ficar mais e mais inclinado. Isso é o que chamamos de efeito de borda.

Quando o fio é infinito (ou quando o comprimento L é muito grande) esses efeitos de borda desaparecem. Assim já podemos eliminar a I e a II

Passo 3

No caso IV fica difícil pensar em que tipo de superfície o campo elétrico é constante já que nesse caso não temos simetria esférica ou cilíndrica.

Ainda que possamos englobar todo o anel com uma superfície gaussiana simétrica fechada qualquer (cilindro ou esfera, por exemplo), o campo elétrico produzido pelas cargas do anel não será o mesmo em todos os pontos dessa superfície fechada. Por isso não dá para encontrar uma expressão analítica explícita para esse caso IV.

Passo 4

Por outro lado, a III nem está nas opções haha. Não conseguimos aplicação útil da Lei nela porque não sendo uniforme também não temos simetria cilíndrica do campo. Se fosse uma distribuição de cargas uniforme, aí sim teríamos esse caso.

Passo 5

Nesse caso aqui não há razão para pensarmos que o campo elétrico não seja radial e dependa somente da distância até o centro da esfera (já que a densidade também depende somente dessa distância radial).

Como o campo elétrico é radial e sua intensidade só depende da distância até o centro da esfera

E → = E r r ^

Podemos escolher como gaussiana uma esfera de raio r de forma que o elemento de área da esfera é

d A → = d A r ^

Assim fica mole aplicar a lei de Gauss

∫ E → ⋅ d A → = E r A r = E r 4 π r 2

Ou seja, nesse caso é conveniente usar a lei de Gauss 😉

Resposta

Letra b

Exercício Resolvido #3

UFRJ-P1-2011.1-ME07.

A figura representa o perfil de uma placa condutora de espessura d finita e demais dimensões muito maiores que d . A densidade superficial de carga σ em ambas as faces da placa é constante (uniforme e estacionária). Considerando as três superfícies cilíndricas indicadas na figura, qual das afirmativas abaixo é correta?

  1. E 1 > E 2 > E 3
  2. E 1 > E 2 = E 3
  3. E 1 = E 2 > E 3
  4. E 1 < E 2 < E 3
  5. E 1 = E 2 = E 3

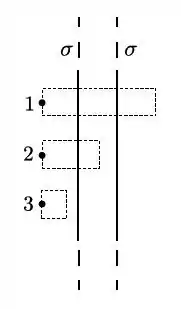
Passo 1

Essa é tiro e queda. Você só tem que entender que o campo em um ponto não depende da superfície que você inventa passando por aquele ponto.

Como se trata de um plano, nós já vimos que o campo é uniforme e estacionário:

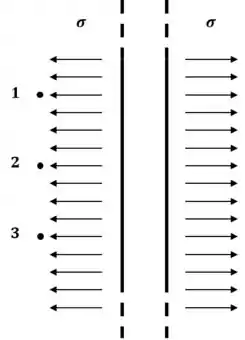
Fiz o desenho considerando densidades σ positivas, por isso o campo sai das placas ao invés de entrar.

Portanto os campos são iguais nos três pontos.

Resposta

Letra e

Exercício Resolvido #4

DEPARTAMENTO DE ENGENHARIA FÍSICA – MATERIAL DE ESTUDO: ELETRICIDADE, MAGNETISMO E CIRCUITOS.

Um elétron se encontra no centro de um cubo cuja aresta mede 20   n m . Calcule o fluxo elétrico através de uma das faces do cubo.

Passo 1

A superfície do cubo é fechada, então podemos tranquilameeente usar a Lei de Gauss para calcular o fluxo elétrico

ϕ = Q i n t ε 0

No caso, Q i n t vai ser a carga do elétron que é - 1,6 × 10 - 19   C e ε 0 é uma constante que vale 8,85 × 10 - 12 C 2 N . m 2 . Agora é só substituir na fórmula :)

Passo 2

Substituindo os valores, temos que

ϕ = - 1,6 × 10 - 19 8,85 × 10 - 12

ϕ = - 1,8 × 10 - 8   N . m 2 / C  

Passo 3

Calma que ainda não acabou, tem só mais um detalhe: Esse fluxo que calculamos pela Lei de Gauss é o fluxo sob toda a superfície fechada do cubo e não o fluxo através de uma única face do cubo, como o exercício pede.

Mas não se desespera, porque como há 6 faces em um cubo e o cubo é simétrico, o fluxo através de uma única face será 1/6 do fluxo total, sacou?

ϕ f a c e = - 1,8 × 10 - 8 6 = - 0,3 × 10 - 8   N . m 2 / C  

Resposta

ϕ f a c e = - 0,3 × 10 - 8   N . m 2 / C  

Exercício Resolvido #5

Site do Prof. A. F. Guimarães, lista 03 de Física 3

Uma carga puntiforme de 1,0 × 10 - 6   C está colocada no centro de uma superfície Gaussiana cúbida, de aresta igual a 0,5   m . Qual o valor de Φ E para essa superfície:

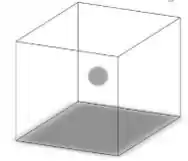
Passo 1

Segundo a lei de Gauss, temos que:

Φ E = Q i n t ϵ 0 ,

onde Q i n t é a carga total dentro da superfície fechada (superfície Gaussiana). Assim, o fluxo será dado por:

Φ E = 1,0 × 10 - 6 8,85 × 10 - 12 ,

Φ E = 1,13 × 10 5   N m 2 C - 1 .

Resposta

Φ E = 1,13 × 10 5   N m 2 C - 1 .

Exercício Resolvido #6

Site do Prof. A. F. Guimarães, lista 03 de Física 3 (modificada)

Numa esfera dielétrica oca existe uma densidade volumétrica de cargas ρ constante. O raio externo da esfera é igual a b e o raio do buraco esférico concêntrico é igual a a , conforme a figura. Determine o fluxo elétrico através de uma gaussiana esférica concêntrica de raio r ≥ b .

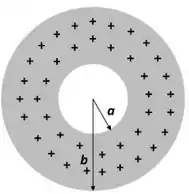
Passo 1

Segundo a lei de Gauss, temos que:

Φ E = Q i n t ϵ 0 ,

onde Q i n t é a carga total dentro da superfície fechada (superfície Gaussiana), dada por:

Q i n t = ρ V T .

Na expressão acima, V T é o volume total, dado por:

V T = 4 π 3 b 3 - a 3 .

Assim, o fluxo será dado por:

Φ E = 4 π ρ b 3 - a 3 3 ϵ 0 .

Resposta

Φ E = 4 π ρ b 3 - a 3 3 ϵ 0 .

Exercício Resolvido #7

TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.

Determine o campo elétrico devido a uma fina casca esférica carregada de raio R e carga total Q .

Passo 1

Nesse caso, a gente tem uma configuração de cargas que só depende da distância até o centro da casca esférica, então a gente tem aqui uma simetria esférica certo?

Isso quer dizer que E → deve ser radial e seu módulo só deve depender da distância r até o centro.

Então vamos escolher pra esse caso uma superfície gaussiana esférica S concêntrica à casca esférica e com um raio arbitrário r beleza? Vamos ter algo parecido com essa imagem

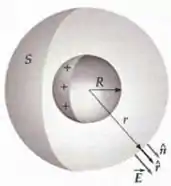
Agora temos que usar a Lei de Gauss e avaliar os casos em que r < R e r > R

Passo 2

A Lei de Gauss é expressada assim

ϕ = ∮ S E n ⅆ A = Q i n t ε 0

Sabendo que o valor de E n é o mesmo em qualquer ponto da superfície gaussiana e que a área da superfície de uma casca esférica é 4 π r ² , podemos escrever que

E n 4 π r ² = Q i n t ε 0

Devido à simetria, E n = E r , então

E r = Q i n t 4 π r ² ε 0

Agora basta avaliar essa expressão quando r < R e quando r > R

Passo 3

Quando r < R , a carga dentro da superfície gaussiana vai ser 0, então

E r = 0 4 π r ² ε 0 = 0

Para r > R , a superfície gaussiana engloba toda a casca esférica, então a carga dentro dela vai ser o próprio Q

E r = Q 4 π r ² ε 0

Resposta

E → = E r r ^ onde E r = 0 ,   r < R Q 4 π r ² ε 0 ,   r > R

Exercício Resolvido #8

TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.

Determine o campo elétrico gerado por uma esfera sólida uniformemente carregada que tem raio R e uma carga total Q , distribuída uniformemente através do volume da esfera cuja densidade de carga é ρ = Q V onde V = 4 π R 3 3 é o volume da esfera.

Passo 1

Temos aqui uma simetria esférica, isso quer dizer que o campo elétrico deve ser radial e iremos escolher uma superfície gaussiana S esférica de raio r . Na imagem da esquerda temos o caso em que r > R e na da direita temos r < R

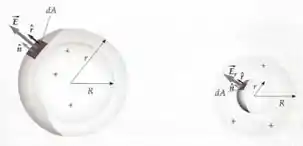
Por simetria, E n = E r e também é constante em qualquer ponto da superfície. Vamos usar a Lei de Gauss para encontrar o campo elétrico nas duas situações das imagens acima ;)

Passo 2

A Lei de Gauss é

ϕ = ∮ S E n ⅆ A = Q i n t ε 0

Como E n é constante e a área da superfície de uma casca esférica é 4 π r ² :

E r 4 π r ² = Q i n t ε 0

E r = Q i n t 4 π r ² ε 0

Agora basta avaliar essa expressão quando r < R e quando r > R

Passo 3

Quando r < R , a carga dentro da superfície gaussiana vai ser

Q i n t =   ρ V '

Onde V ' = 4 π r 3 3 , então

Q i n t = Q V 4 π r 3 3

Q i n t = Q 4 π R 3 3   4 π r 3 3

Q i n t = Q r 3 R 3

Então, o campo elétrico para r < R vai ser

E r = Q r 3 R 3 4 π r ² ε 0

E r = Q r R 3 4 π ε 0

Para r > R , a superfície gaussiana engloba toda a casca esférica, então a carga dentro dela vai ser Q mesmo

E r = Q 4 π r ² ε 0

Resposta

E → = E r r ^ onde E r = Q r R 3 4 π ε 0 ,   r < R Q 4 π r ² ε 0 ,   r > R

Exercícios de Livros Relacionados

Explique por que a intensidade do campo elétrico aumenta linearmente com r no lugar de decrescer com inverso de r 2 entre o centro e a superfície de uma esfera sólida carregada uniformemente.
Como as fórmulas para a lei da gravidade de Newton e para a lei de Coulomb têm a mesma dependência com o inverso do quadrado da distância, uma fórmula análoga à da lei da Gauss pode ser determinada pa
Uma casca uniformemente carregada com densidade volumétricaρ contém em seu interior uma cavidade esférica. Mostre que o campo no interior da cavidade é uniforme e é dado por E → = ρ d → 3 ϵ 0 , onde d
Qual é o fluxo elétrico através de um dos lados de um cubo que tem uma carga puntiforme isolada de - 3,00μ C colocada no seu centro? Dica: você não precisa integrar nenhuma equação para obter a respos
Medidas cuidadosas do campo elétrico na superfície de uma caixa preta indicam que o fluxo elétrico resultante saindo da superfície da caixa é 6,0k N ⋅ m 2 / C . (a) Qual é a carga resultante dentro da