Forças Conservativas

Teoria

Opa, seja muito bem vindo ao Responde Aí! Bora bater um papo sobre forças conservativas?!

O que são Forças Conservativas?

As forças conservativas são aquelas que não fazem o sistema perder energia, como por exemplo a força peso, a força elástica e também a força elétrica! Aqui na física mecânica a gente vai focar na força peso e na força elástica! Beleza?

-Beleza, mas e na prática…qual diferença vai fazer se a força é conservativa ou não?

Eu vou responder essa pergunta com uma outra pergunta! Se liga no desenho abaixo, após os carrinhos e , ambos de massa , percorrerem todo o seu caminho. Em qual caso o trabalho da força peso será maior?

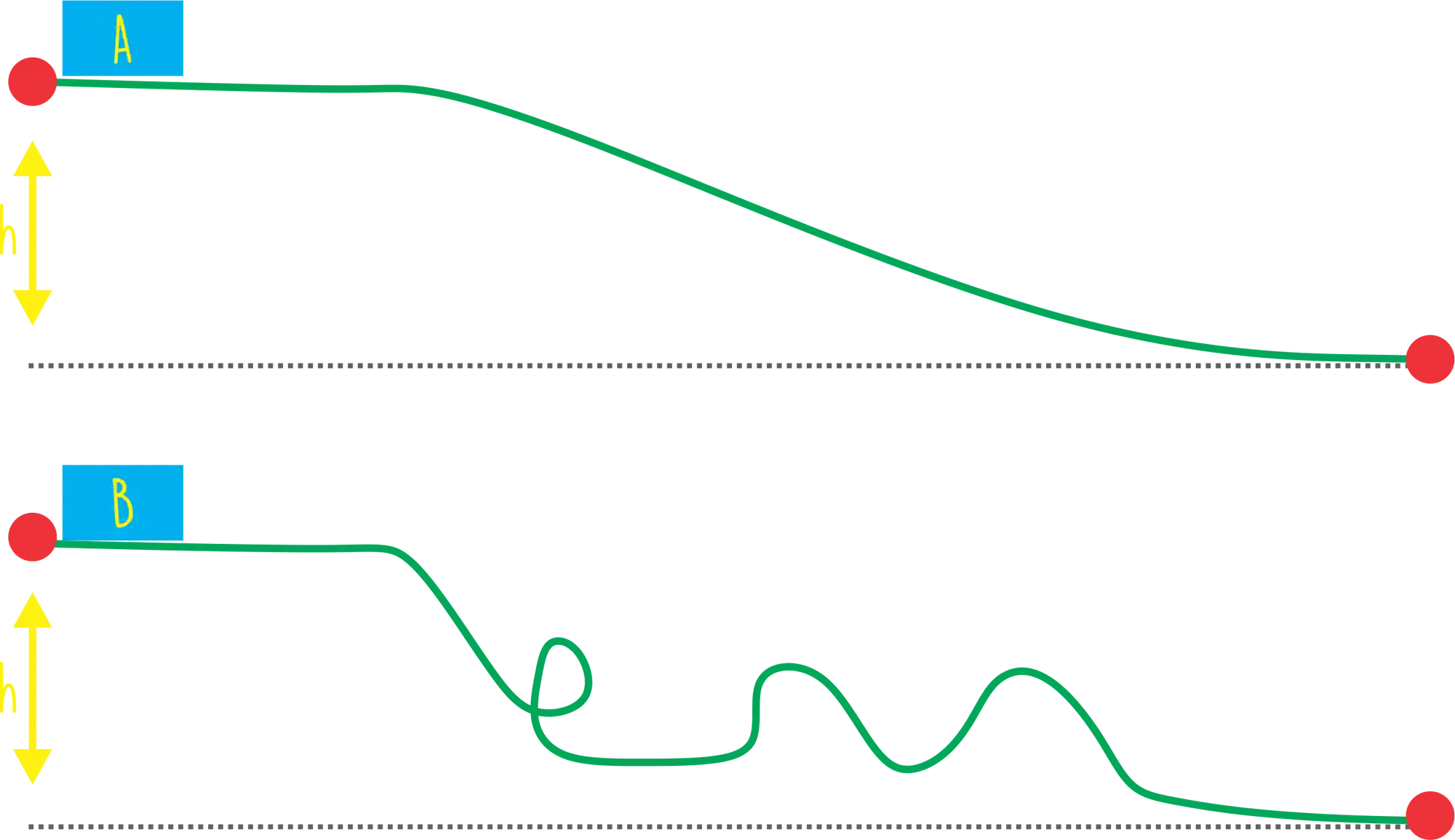
E se eu te falar que em ambos os casos o trabalho da força peso vai ser igual?! 😱

Exatamente! O trabalho da força conservativa não depende do caminho, apenas da posição final e a posição inicial!

📢 Clique para ver mais:

-Beleza, mas como eu uso isso na prática?!

Calma que a gente vai falar tudinho que você precisa saber! Mas bora começar assistindo esse vídeo completaço sobre forças conservativas que o Responde Aí preparou pra você?

Trabalho da Força Peso

Como vimos ali em cima, as forças conservativas conservam a energia mecânica do sistema. Isso quer dizer que é dada por:

Onde K e U são as energias cinética e potencial do sistema, respectivamente. Nesse caso, a variação da energia mecânica será a soma das variações de cada energia, tal que:

E o trabalho realizado pela força no sistema, será dado como:

Mas como acabamos de ver, quando temos uma força conservativa atuando no sistema, a variação de energia mecânica é zero, então:

Então quando uma força conservativa atua em um sistema, o trabalho que ela realiza está diretamente ligado a energia potencial do sistema, através da relação:

Ou seja, o trabalho realizado por uma força conservativa é igual ao negativo da variação de energia potencial!

Trabalho da Força Elástica

Agora vamos conferir porque a força elástica é uma força conservativa! Para isso vamos provar que o seu trabalho não depende do caminho.

A força elástica é dada pela seguinte fórmula:

Onde é a constante da mola e é o seu deslocamento. O trabalho realizado pela força elástica atuando em um corpo entre e é dado por:

Aqui e podem representar a deformação da mola ou sua elongação. Se calcularmos , temos:

Portanto o trabalho de ida somado com o trabalho de volta é igual a zero. Ou seja, a força elástica é conservativa!

Agora vamos praticar com exercícios?

Trabalho da Força Peso

Trabalho da Força Elástica

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-Física 1-Prova 1 2012.2 Múltipla Escolha n°4

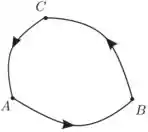
Uma partícula move-se sob a ação de uma única força conservativa , no percurso fechado , como indica a figura abaixo. Afirma-se que para o trabalho desta força nos trechos , e :

Como a força é conservativa o trabalho desta força é sempre positivo em qualquer trecho e sentido do percurso.

A opção correta para as afirmativas I), II), III) e IV) é:

Somente I) e II) estão corretas;
Somente II) e IV) estão corretas;
Somente I) e III) estão corretas;
Somente I), II) e III) estão corretas;
Todas estão corretas

Passo 1

Vamos analisar cada afirmação

verdadeiro, como temos uma força conservativa, e ele volta ao mesmo ponto o trabalho vai dar zero

Passo 2

verdadeiro, invertendo o caminho seria como inverter o sentido do deslocamento, tornando igual a outra em módulo mudando seu sinal

Passo 3

verdadeiro, em forças conservativas não importa o caminho, só importa o ponto inicial e o final

Passo 4

falso, se a força estiver contrária ao movimento o trabalho será negativo

Resposta

Letra D

Exercício Resolvido #2

UFRJ-Física 1-Prova 1 2015.1 Múltipla Escolha n°2

Afirma-se sobre forças conservativas:

I) O trabalho realizado por forças conservativas sobre uma partícula ao deslocá-la de uma posição inicial a uma posição final é independente da trajetória seguida.

II) Uma força é conservativa se o trabalho desta força ao longo de uma trajetória fechada qualquer é nulo.

III) A energia potencial associada a uma força constante e diferente de zero também é uma constante.

São corretas as afirmativas

(a) I), II) e III);

(b) I) e III);

(d) I) e II) ;

(e) Nenhuma das afirmativas está correta.

Passo 1

Afirmativa I):

Essa é justamente uma das definições mais usadas para uma forças conservativa.

Certíssimo!!!

A afirmativa está correta! ;)

Passo 2

Afirmativa II):

Uma trajetória fechada significa que o ponto de chegada é o mesmo que o ponto de saída. E como vimos na afirmativa I), o trabalho de uma força conservativa não depende da trajetória.

Então se uma força conservativa atua ao longo de uma trajetória fechada, o trabalho que ela realiza é o mesmo que o trabalho que ela faria se não houvesse nenhum deslocamento. E sem deslocamento não há trabalho, então a afirmativa está correta!

Passo 3

Afirmativa III):

A relação entre força e energia potencial é dada por:

é a derivada da energia potencial em relação ao tempo, com o sinal trocado.

Aqui ele disse que a força é constante e diferente de zero. Então não pode ser uma constante, porque se fosse, sua derivada daria zero, e consequentemente, também.

Talvez você ainda não tenha visto muito bem derivadas em cálculo, mas a derivada de uma constante sempre dá zero, então e não podem ser os dois constantes, com .