Equação de Bernoulli
Produzido por Leonardo de BemTeoria
Equação de Bernoulli descreve o comportamento do escoamento de um fluido. Ela é obtida a partir do Teorema da Conservação de Energia Mecânica.
Pra ficar mais claro, se liga nessa imagem aqui:
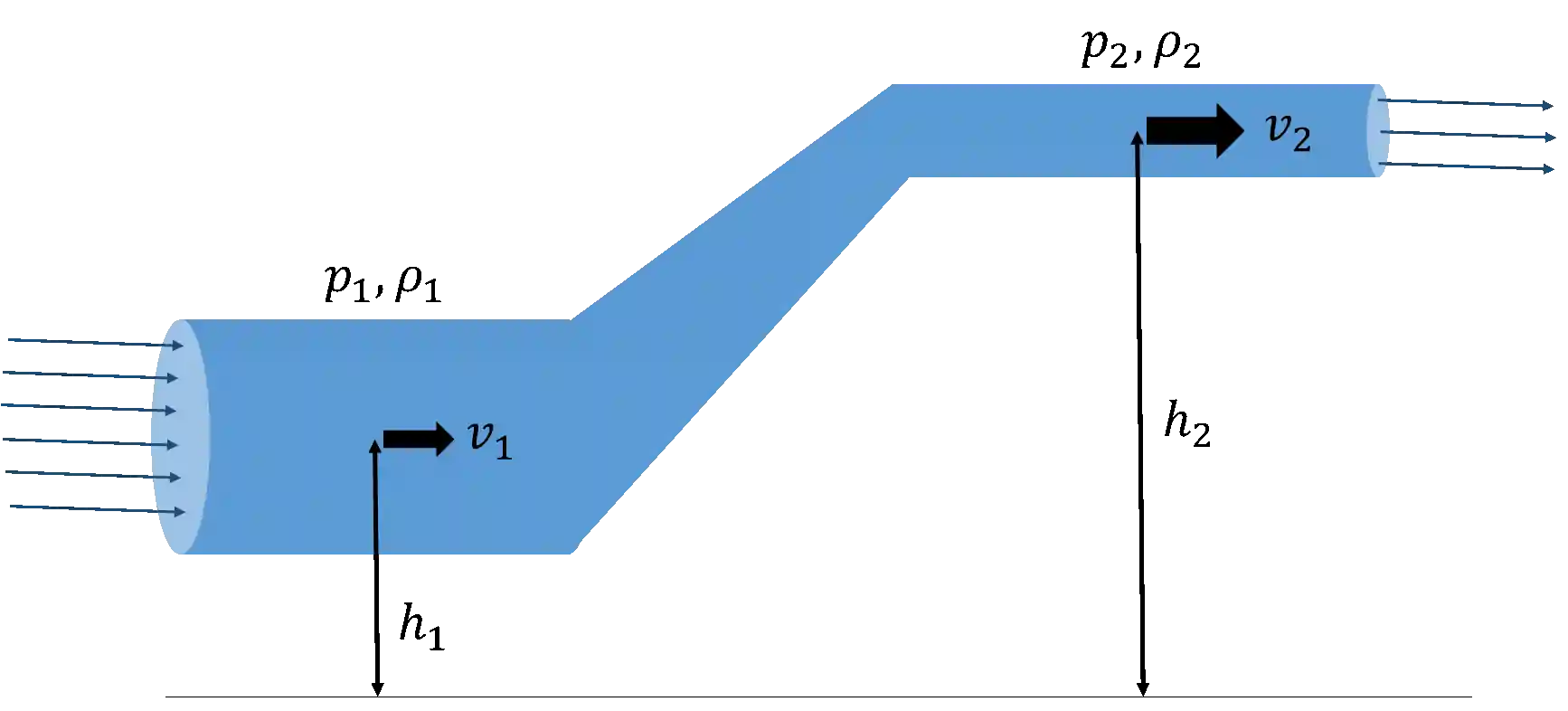
No ponto (1), temos um fluido de densidade
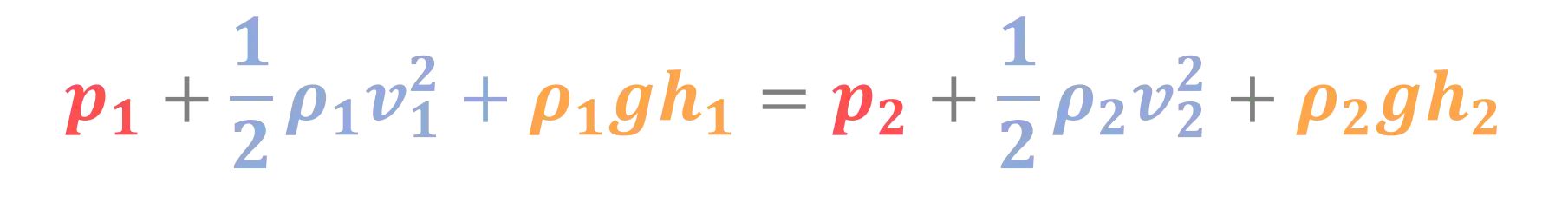
Onde:
A fórmula é bem grandinha, mas as variáveis dela são bem conhecidas, então aqui vai uma dica! Como estamos falando de uma soma, cada conjunto coloridinho da fórmula acima tem que ter a mesma unidade que os outros, nesse caso unidade de pressão!
Ou talvez você encontre a equação de Bernoulli representada dessa forma aqui:
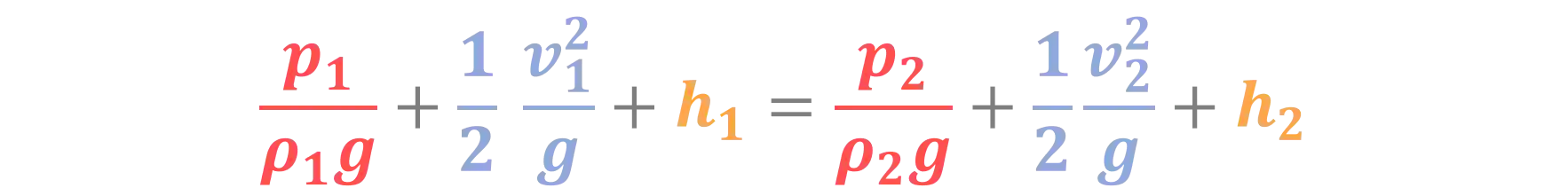
Nesse caso dividimos tudo por
Se liga nesse vídeo super completo sobre Equação de Bernoulli, que o Responde Aí preparou pra você 🧡
📢 Clique para saber mais:
Quais são as condições para a aplicação da equação de Bernoulli?
Para a gente poder aplicar a equação de Bernoulli, temos que considerar algumas hipóteses:
- Escoamento em regime permanente;
- Escoamento incompressível (Densidade constante ao longo do escoamento);
- Escoamento sem viscosidade.
Exercício: Calcule o
Bora aplicar os conhecimentos em um exemplo pra tudo ficar mais claro?!
Pra isso a gente vai considerar o escoamento que vimos lá em cima e vamos calcular a diferença de pressão entre os pontos
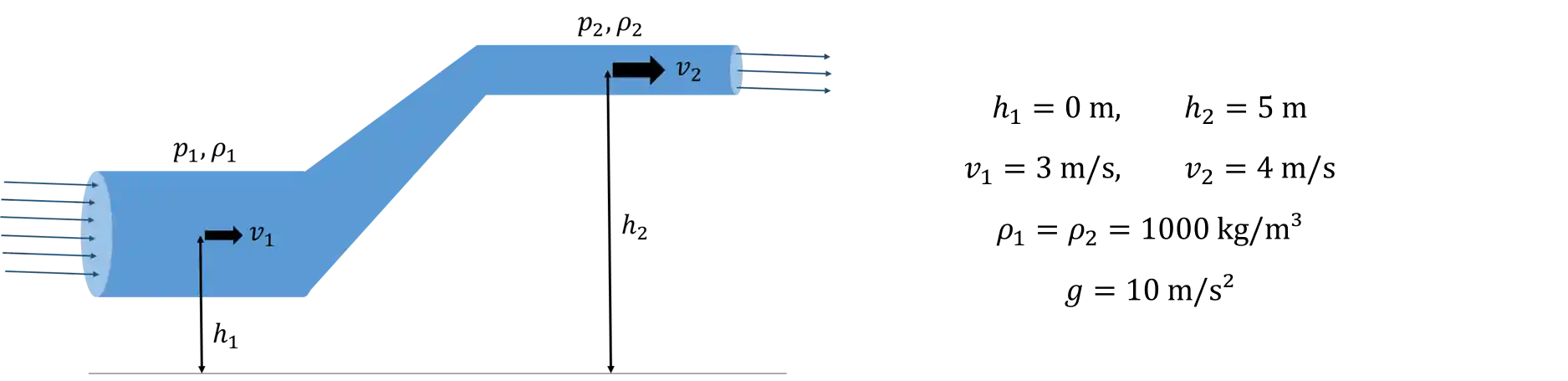
Pra isso vamos isolar
Como
Calculamos, chegamos em:
Ou seja, se a variação de pressão foi negativa, quer dizer que a pressão do ponto
Só que se a gente olhar a imagem do exemplo, vemos que o diâmetro do ponto
Mas não! 😱😱😱
Como o avião se sustenta no ar?
Quando comparamos dois pontos, em um escoamento contínuo, quanto maior for a velocidade de um ponto, menor será sua pressão! Essa característica da equação de Bernoulli explica porque os aviões se mantêm no ar!!!
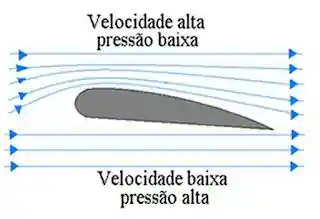
Na imagem acima vemos um esquema da asa de um avião. Podemos observar que como a parte de cima é curvada o caminho que o vento tem que percorrer é maior. Como o escoamento é contínuo, o ar que percorre a parte superior da asa deve chegar junto com o ar que percorre a parte inferior da asa. Dessa forma a velocidade do vento na parte superior da asa deve ser maior, consequentemente teremos uma pressão mais baixa na parte superior da asa em comparação com a inferior, fazendo com que o avião se sustente no ar!
Maneiro, não é?! Agora vamos praticar com exercícios resolvidos?