Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 62
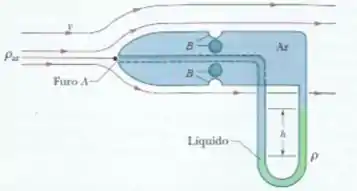
O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos (quatro são mostrados na figura) que permitem a entrada de ar no tubo; esse tubo está ligado a um dos lados de u tubo em forma de U. O outro lado do tubo em forma de U está ligado ao furo na frente do medidor, que aponta no sentido do movimento do avião. Em , o ar fica estagnado, de modo que . Em , porém, a velocidade do ar é presumivelmente igual à velocidade do ar em relação ao avião. (a) Use a equação de Bernoulli para mostrar que
Onde é a massa específica do líquido contido no tubo em U e é a diferença entre os níveis do líquido no tubo. (b) Suponha que o tubo contém álcool e que a diferença de nível é . Qual é a velocidade do avião em relação ao ar? A massa específica do ar é e a do álcool é .
Passo 1
A letra (a) quer que a gente use a equação de Bernoulli pra demonstrar aquela relação. Então vamos por partes. Primeiro lembrando como é a equação:
Vamos dizer que o termo esquerdo vai ser aplicado ao furo , e o termo da direita vai ser aplicado ao furo , que deixa o ar entrar naquele tubo maior.
Passo 2
No furo nós temos uma pressão que não conhecemos, e o enunciado diz que a velocidade é , além disso, temos a liberdade de definir que a altura ali é .
A aí o lado esquerdo da equação de Bernoulli fica:
No furo , nós também temos uma pressão que não conhecemos, mas a velocidade é a velocidade do ar em relação ao avião (já que o furo permite a passagem do ar), já a altura pode ser a mesma do furo , então .
E assim ficamos com:
Obs.: No lado direito da equação usamos a densidade do ar porque é sobre ele que estamos aplicando a equação de Bernoulli no furo .
O problema agora é dar um jeito de calcular aquela diferença . Mas é pra isso que serve aquele tubo em U!
Veja que o furo se comunica diretamente com o lado direito do tubo, e o furo se comunica com o lado esquerdo do tubo, ou seja, aquela diferença de altura se deve à diferença de pressão entre os dois lados do tubo:
Onde é a densidade do líquido verde.
Voltando na equação de antes, ficamos com:
Pronto, está demonstrada a fórmula.
Passo 3
A letra (b) basicamente dá um monte de valores que a gente pode jogar na nossa fórmula pra achar a resposta.
Eles disseram que vai ser a densidade do álcool, ou seja, , que a altura do desnível vai ser , e que a densidade do ar é .
Agora vamos substituir tudo isso pra achar a velocidade :
Pronto!
Resposta
(a) Demonstração
(b)