Teorema de Stevin
Teoria
O Teorema de Stevin, também chamado de Lei fundamental da hidrostática serve para calcular a variação de pressão entre dois pontos de um fluido, com alturas diferentes.
O que diz o Teorema de Stevin
Teorema de Stevin diz que:
"A diferença entre as pressões de dois pontos de um fluido em equilíbrio é igual ao produto entre a densidade do fluido, a aceleração da gravidade e a diferença entre as profundidades dos pontos."
Se liga na imagem abaixo:
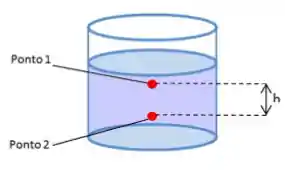
Podemos usar o princípio de Stevin para calcular a diferença de pressão entre os pontos
Onde:
é a diferença de pressão entre os pontos e , em pascal ; é a diferença de altura entre os pontos e , em metro ; -
é a densidade do fluido, em ; é a aceleração da gravidade, medida em .
Se liga nesse vídeo super completo, sobre o Teorema de Stevin, que o Responde Aí preparou pra você arrasar na prova! 👇👇👇
Ou se você preferir, continua comigo no textinho! 👇
Princípio de Pascal - Vasos Comunicantes
O princípio de Pascal diz que:
“O acréscimo de pressão produzido num líquido em equilíbrio transmite-se integralmente a todos os pontos do líquido”.
Na prática Pascal pega o princípio de Stevin e aplica em sistemas como de vasos comunicantes. Pra ficar mais claro se liga nesse elevador hidráulico:
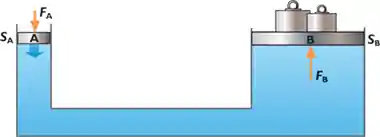
O lado
Segundo o princípio de Pascal, se eu aplico uma pressão do lado
A pressão é igual a razão entre força e a área e a área do lado esquerdo do elevador hidráulico é muito maior do que a do lado direito. Guarda essa informação!
Pelo teorema de Stevin podemos dizer que:
Considerando que os pontos
Ou seja, eu posso aplicar uma força pequenininha em uma área pequena do lado esquerdo e essa força vai ser capaz de movimentar cargas pesadas do lado direito. É assim que funciona o elevador hidráulico!
Agora, vamos praticar com exercícios?!
Princípio de Pascal - Vasos Comunicantes
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
A respeito da lei de Stevin, marque o que for correto:
a) Determina a pressão exercida somente por líquidos.
b) Depende da densidade do recipiente, altura da coluna de líquido e aceleração da gravidade.
c) Determina a pressão exercida por um fluido.
d) Só serve para determinar a pressão exercida pela água.
e) Todas as alternativas estão corretas.
Passo 1
O princípio de Stevin nos diz que, em um mesmo fluido, a pressão exercida dependerá somente da altura!! Ou seja, dois pontos nesse mesmo fluido terão a mesma pressão se estiverem em alturas iguais, indepedentemente de qualquer outra coisa (como o formato do recipiente, por exemplo). Logo, ele é usado para determinar a pressão exercida por um fluido!! E a alternativa (c) nos diz isso.
Resposta
Alternativa (c).
Exercício Resolvido #2
UFRJ-P1-2014.2-4
Considere um fluido incompressível em repouso num recipiente como mostrado na figura. São escolhidos três elementos infinitesimais de área, todos a mesma profundidade, mas com orientações diferentes (. O que podemos dizer sobre a pressão em cada uma dessas superfícies?
- A pressão no elemento orientado para cima é a maior.
- A pressão no elemento orientado para a direita é a menor.
- A pressão nos três elementos é a mesma.
- A pressão no elemento oblíquo é a maior.
- A pressão no elemento orientado à direita é a maior.
Passo 1
Vamos lá!
O que sabemos a cerca de uma pressão num fluido em relação a profundidade do mesmo?
Simples, que ela é a mesma pra todos os elementos que estão a mesma altura.
Esse é o princípio de Stevin. Então a resposta é a c).
Passo 2
Mas isso vai um pouco contra o nosso conhecimento de orientação de área, né?
Porque ali temos 3 elementos com áreas orientadas de formas diferentes. Você poderia pensar: bem, a pressão sempre atua só na vertical, de cima para baixo. Então o elemento 3, por exemplo, não teria pressão em sua área já que ele não está orientado com a vertical.
Porém, isso não é verdade, porque a afirmativa que a pressão depende apenas da altura é muito forte.
Ela depende apenas da altura, e é a mesma pra elemento com alturas iguais e, além disso, como mostra essa questão, ela é a mesma em todas as direções.
Resposta
c)
Exercício Resolvido #3
Elaboração própria
Certa quantidade de água é colocada em um tubo em forma de U, aberto nas extremidades. Adiciona-se um líquido de densidade maior que a da água em um dos lados do tubo e ambos não se misturam.
Assinale a alternativa que representa corretamente a posição dos dois líquidos no tubo após o equilíbrio.
a)
b)
c)
d)
e)
Passo 1
De acordo com princípio de Stevin, pontos de mesmo líquido que estão na mesma altura possuem a mesma pressão sobre eles. Então, no ponto A da horizontal que passa pela interface entre a água e o líquido mais denso, a pressão deve ser a mesma que no ponto B. Vamos ver um esqueminha:
Como a pressão é dada por: , temos que:
Como , . Logo, nosso esqueminha estava certo haha e a resposta é a letra (d).
Resposta
Alternativa (d).
Exercício Resolvido #4
Halliday, Vol 2, Capítulo 14, 9ª edição, exercício 10, página 80
O tubo de plástico da figura abaixo tem uma seção reta de . Introduz-se água no tubo até que o lado mais curto (de comprimento ) fique cheio. Em seguida, o lado menor é fechado e mais água é despejada no lado maior. Se a tampa do lado menor é arrancada quando a força a que está submetida excede , que altura da coluna de água do lado maior deixa a tampa na iminência de ser arrancada?
OBS.: use
Passo 1
Pelo Princípio de Stevin, sabemos que as pressões nos pontos A e B serão iguais:
E podemos relacionar a pressão no ponto B com a equação:
Onde será a altura da coluna de água acima desse ponto.
Passo 2
Bom, na situação descrita, nós vamos ter uma coluna d’água exercendo uma pressão no lado mais curto, para arrancar a tampa, logo, temos umas força associada a essa pressão. E o enunciado diz que a força na iminência da tampa ser arrancada vale e que o tubo de plástico tem uma seção reta de . A pressão e a força vão se relacionar por:
Agora, usando as duas equações encontradas:
Passo 3
Calma calma, ainda não terminou: esse valor de é a altura a partir do ponto B, lembra? Então, nossa verdadeira altura (do chão) vale:
Agora sim hehe acabamos a questão.
Resposta
A altura da coluna de água vale .
Exercício Resolvido #5
Halliday, Física 2, Capítulo 17, 4ª edição, exercício 13, página 76.
Um tubo em U simples contém mercúrio. Quando de água são derramados no ramo esquerdo, a que altura sobe o mercúrio no lado direito, com relação ao seu nível inicial?
Considere
Passo 1
Pela figura, queremos descobrir a distância , isto é, a diferença entre a nova altura do mercúrio no lado direito com relação ao nível inicial, ilustrado na primeira figura.
Para isso, aplicamos o Princípio de Stevin: igualamos as pressões de um mesmo fluido a uma mesma altura.
Neste caso, vamos igualar as pressões nos pontos (1) e (2), que correspondem à interface entre os fluidos no lado esquerdo e o ponto correspondente no lado direito:
Logo:
Passo 2
Vamos calcular as pressões e :
Calculando :
onde , conforme o enunciado falou, e é a densidade da água:
Calculando :
onde é a densidade do mercúrio.
Passo 3
Igualando as pressões:
Passo 4
Substituindo os valores:
Passo 5
Agora, para calcular , temos que parar um segundo pra perceber uma coisa:
A quantidade total de mercúrio é fixa!
Ou seja: o mercúrio se deslocou mas a quantidade total de fluido não se alterou. Portanto, tudo o que desce no lado esquerdo, necessariamente tem que subir no lado direito!
Pois estamos supondo, também, que o líquido não se comprime nem se distende, ou seja, é um líquido incompressível:
Percebeu?
Se o líquido sobe no lado direito, então ele desceu no lado esquerdo.
Pela figura, podemos ver então o seguinte:
Pronto! Como já calculamos , agora ficou fácil:
Resposta
Exercício Resolvido #6
UFRJ-Questão 2 - P1.2015
Em um tubo em U, com ambas as extremidades abertas para a atmosfera, coloca-se cuidadosamente três líquidos de densidades diferentes , e , de forma que estes não se misturam. Após o equilíbrio ser atingido, a disposição dos líquidos é a ilustrada na figura. A relação entre as densidades dos líquidos 1 e 3 é:
Passo 1
Vamos usar o princípio de Stevin aqui: A pressão na interface dos líquidos de densidades e com o ar atmosférico deve ser a mesma já que estão sob a pressão atmosférica.
Outro detalhe importante é presença do fluido . O princípio de Stevin diz que devemos fazer comparações em um mesmo fluido, não é mesmo?
Pois bem, se compararmos as pressões nas interfaces dos líquidos, estaremos fazendo a comparação de pressões no mesmo líquido: , já que ele possui duas interfaces: uma com e outra com .
Passo 2
Beleza. A pressão devido à é dada por:
E a pressão causada por é dada por:
Como:
Temos que:
Resposta
a)
Exercício Resolvido #7
Lista de exercícios, UNIP, modificado
No sistema abaixo, sabe-se que . Determinar a densidade do líquido.
São dados:
Considere e
Passo 1
Queremos encontrar a densidade do líquido à direita.
Para isso, aplicamos o Princípio de Stevin: igualamos as pressões de um mesmo fluido a uma mesma altura.
Neste caso, vamos igualar as pressões nos pontos (1) e (2), que correspondem à interface entre os fluidos no lado direito e o ponto correspondente no lado esquerdo:
Logo:
Passo 2
Vamos calcular as pressões e :
Calculando :
onde e são dados e é a densidade da água:
Convertendo para metros:
Observe que .
Convertendo para :
Calculando :
onde é a densidade do líquido, é a pressão atmosférica e é dado do problema.
Convertendo para metros:
Passo 3
Igualando as pressões:
Passo 4
Substituindo os valores:
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 94 – Modificado
O líquido no manômetro de tubo aberto indicado na figura abaixo é o mercúrio, e . A pressão atmosférica é igual a
- Qual é a pressão absoluta no fundo do tubo em forma de
- Qual é a pressão absoluta no tubo aberto a uma profundidade de abaixo da superfície livre?
- Qual é a pressão absoluta do gás em pascals?
Dados:
Passo 1
a):
Bom pessoal, o enunciado está pedindo a pressão no fundo do Tubo em U.
Qual a melhor forma de se fazer isso?
Bem, como a pressão só depende da altura, basta a gente calcular a pressão no lado direito da figura, ou seja, no lado do tubo aberto pra atmosfera.
Beleza? Essa pressão será a mesma para todo o fundo, já que ela só depende da altura.
Assim:
Passo 2
Muita calma agora! Vamos converter o valor da pressão do enunciado, que está em milibares, para
Assim:
Show! Agora podemos continuar com a nossa questão.
A pressão no fundo vai ser igual a pressão da coluna de mercúrio mais a pressão atmosférica(lembrando que o da fórmula vai ser igual a
Passo 3
b):
Essa vai ser bem parecida com a a).
Agora queremos a pressão a uma profundidade de abaixo da superfície do líquido. Então, qual será o nosso
Isso ai:
Assim:
Passo 4
c):
Agora vamos usar de novo o conceito que aprendemos na teoria: O fluido tem pressões iguais em altura iguais!
Vamos considerar dois pontos: Um ponto na superfície do líquido que está em contato com o gás, na esquerda, e um ponto no tubo aberto, na direita, que tenha a mesma altura:
A pressão no ponto da esquerda, vai ser causada apenas pelo gás, enquanto a pressão do lado direito, será causada pela coluna de líquido e pela pressão atmosférica.
Assim:
E
Passo 5
Olhando a figura do enunciado, nós podemos notar que a altura da coluna de líquido que causa a pressão é dada por:
Assim:
Então a pressão do gás vale:
Resposta
a):
b):
c):