Energia Potencial Gravitacional
Teoria
No estudo de energia, aprendemos sobre a energia potencial gravitacional. No entanto, como estávamos tratando de corpos na superfície da Terra, para calcular a energia potencial, considerávamos a aceleração da gravidade na superfície ().
Agora iremos expandir esse conceito para caso mais geral. Não se assuste, vamos devagarzinho.
A definição da energia potencial gravitacional é:
Onde é a constante gravitacional, é a massa que está sendo analisada, que está se aproximando/afastando de uma massa , e está a uma distância desta.
“Mas por que diabos tem um sinal de menos ali??!!”
Diferentemente da outra energia potencial gravitacional, esta consideramos zero lá no infinito (quando ). Quando o corpo vai se aproximando da terra (), a energia vai diminuindo também, já que vai se tornando mais negativa.
Vamos a um exemplinho simples:
Uma massa está a uma distância de outra massa e possui energia gravitacional . Determine a que distância deve estar a massa para que sua energia potencial seja .
Primeiramente vamos encontrar a relação entre e o restante das variáveis:
Para que :
Portanto:
Lembre-se de tomar cuidado com o sinal de menos, pois, neste caso, apesar de o módulo ter ficado menor, a energia potencial gravitacional aumentou, já que se tornou menos negativa.
Se manda pros exercícios e bora praticar!
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física II – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, p. 29 ex. 26- Modificado.
Dez dias após seu lançamento para Marte em dezembro de 1998, a espaçonave Mar Climate Orbiter (massa igual a ) estava a uma distância de da Terra e se deslocava com velocidade igual a em relação à Terra. Nesse momento, qual era a energia potencial gravitacional do sistema espaçonave-Terra?
Dados:
Passo 1
Acabamos de aprender a fórmula para energia potencial gravitacional:
Passo 2
Temos os seguintes dados:
(Considera-se essa a distância da espaçonave até o centro da Terra)
Substituindo-os, teremos:
Resposta
Exercício Resolvido #2
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 400 ex. 46- Modificado.
a) Se tomamos como zero a energia potencial de um corpo de e a Terra, quando os dois estão separados de uma distância infinita, qual é a energia potencial quando o corpo está na superfície da Terra?
b) Determine a energia potencial do mesmo corpo a uma altura, acima da superfície da Terra, igual ao raio da Terra.
Dados:
Passo 1
a) Já sabemos a fórmula para energia potencial gravitacional para quando ela é zero no infinito:
Quando o corpo está na superfície da Terra, temos:
Logo, substituindo os dados, temos:
Passo 2
b) Quando o corpo está numa altura acima da superfície da Terra igual ao seu raio, teremos:
Logo:
Resposta
a)
b)
Exercício Resolvido #3
UNICAMP-P1-2012-3
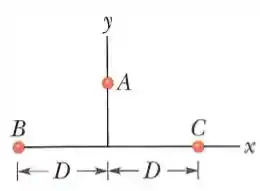
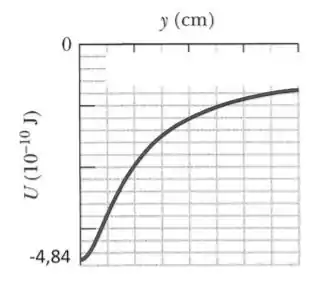
Uma partícula (partícula , de massa ) pode ser deslocada ao longo de um eixo desde uma distância infinita até a origem. A origem está localizada no ponto médio entre as partículas e , que têm massas iguais , e o eixo é perpendicular à linha que liga essas duas partículas. A distância é . O gráfico mostra a energia potencial do sistema de três partículas em função da posição da partícula no eixo , sendo que para a direita a curva tende assintoticamente ao valor de quando . Quais são os valores de e ?
.
Passo 1
Sabemos que a energia potencial gravitacional, no sistema mostrado, é dada por:
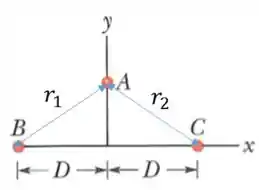
Mas, vendo a imagem, descobrimos que:
E, colocando em função de e :
Portanto, a expressão da energia é dada por:
Passo 2
Agora, com a expressão da energia do sistema, fica fácil!
Pelo gráfico, sabemos que, quando , a energia é , então:
Já para , temos que a energia é , então:
Sabendo que , podemos usar a segunda equação para encontrar o valor de :
Usando esse valor na primeira expressão: