Força Gravitacional
Produzido por Ludovic BeghinTeoria
A força gravitacional é uma força atrativa que existe entre todos os corpos com massa!
Ela é o motivo da gente não sair flutuando por ai, das coisas caírem no chão e até da gente conseguir respirar! Afinal o centro da terra atraí até a atmosfera! 🙃
Pra você aprender tudo o que você precisa saber sobre força gravitacional e arrasar na prova, se liga nesse vídeozinho que o Responde Aí preparou especialmente pra você 👇 🧡
Ou continua comigo no textinho! 👇
Lei da Gravitação Universal
A lei da gravitação universal diz que entre dois corpos de massa
Onde,
-Beleza! Mas se existe atração entre dois corpos quaisquer, então como a gente não sente isso no dia a dia?!
Excelente pergunta! E na verdade a gente sim, é a força gravitacional que segura a gente no chão. Mas eu entendi a sua dúvida, seria “porque a gente não sente a força gravitacional com objetos da terra”, é isso?
Bem, antes de qualquer coisa, é importante notar que a força gravitacional é:
- Inversamente proporcional ao quadrado da distância entre os objetos; ou seja, quanto mais afastados os objetos estão menor será essa força;
- Diretamente proporcional ao produto das massas dos dois objetos; ou seja, quanto maior o produto das massas maior vai ser essa força;
A força gravitacional atua em qualquer corpo, não necessariamente apenas em corpos celeste, o que acontece é que a constante gravitacional
Sacou?!
Mas se você ainda não tiver convencido, se liga nesse exemplo! 👇
Exemplo: Qual será o valor da força gravitacional entre duas vaquinhas?!
Sejam duas vaquinhas de massa
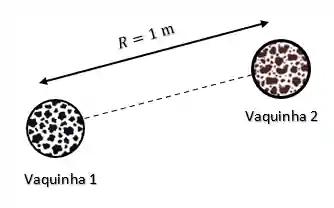
Para sabermos o valor da força gravitacional que a vaquinha
Substituindo os dados:
Calculando:
Ou seja, uma força muito fraquinha, que não consegue atrair nem um mosquito! 🦟
Por isso trabalhamos usualmente com forças gravitacionais de corpos bem mais pesados!
Campo gravitacional
Outro conceito que é muito citado em exercícios é o de campo gravitacional ou aceleração gravitacional!
Sempre que a gente tiver uma força gravitacional atuando em um sistema, teremos um campo gravitacional associado. Bora ver isso melhor, se liga só:
Imagina que uma massa
Usando a segunda lei de Newton, temos que:
Igualando as equações, temos:
Essa aceleração
Aqui na Terra, temos um campo gravitacional que exerce força sobre a gente, direcionado para o centro:
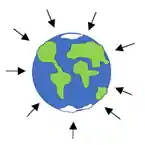
Conseguimos descobrir o valor da gravidade, sabendo que, a massa da Terra, igual a
Calculando:
Que é exatamente o valor que a gente usa no dia a dia!
Exercício Resolvido
Pra fechar com chave de ouro, se liga nesse exercício resolvido em vídeo, sobre força gravitacional, que a gente preparou pra você 🧡
Agora vamos praticar com mais exercícios?!
Campo gravitacional
Exercício Resolvido
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física II – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, p. 28 ex. 4
Duas esferas uniforme, cada uma com massa e raio , estão em contato. Qual é o módulo da força de atração gravitacional entre elas?
Passo 1
Aprendemos a concentrar toda a massa de esferas em seus centros, portanto, o problema se transformaria em duas cargas pontuais de massa , e com uma distância uma da outra.
Aplicando a fórmula da força gravitacional, temos:
Resposta
Exercício Resolvido #2
UFRJ-PF-2015.1-ME7
Duas partículas, cada uma de massa , separadas por uma distância interagem com força gravitacional de módulo . Duas outras partículas, cada uma de massa , separadas por uma distância interagem com força gravitacional de módulo
(a)
(b)
(c)
(d)
(e)
Passo 1
A fórmula geral da força gravitacional entre 2 partículas de massa M e que são separadas por uma distância é:
onde é a constante gravitacional.
Passo 2
Então, já que as duas primeiras partículas têm massa e são separadas por uma distância , o módulo da força gravitacional entre elas é:
Passo 3
Sendo o módulo da força gravitacional entre as partículas de massa separadas por uma distância , temos:
É o mesmo que pras outras partículas!
Resposta
Alternativa (a)
Exercício Resolvido #3
Randall D. Knight, Física Uma Abordagem Estratégica – Volume 1, 2a ed. Porto Alegre: Bookman, 2009, pp 393 – Pare e Pense 13.3
Um planeta tem massa quatro vezes maior do que a da Terra, mas a aceleração da gravidade em sua superfície é a mesma que na superfície da Terra. O raio do planeta é:
Passo 1
Podemos assumir direto a fórmula da gravidade na superfície de um planeta, mas se ainda não está decorado, vamos deduzi-la de acordo com a fórmula da gravidade (esta é a mais importante!).
Passo 2
Tendo, agora, a fórmula da gravidade na superfície de um planeta, basta aplicarmos os valores dados no enunciado.
Para a Terra:
Para o planeta:
Igualando as fórmulas, visto que a gravidade é a mesma, temos:
Resposta
Letra b)
Exercício Resolvido #4
Lista 11, questão 2 – Gravitação, Universidade Federal Fluminense, 2014
Sabendo que a aceleração da gravidade na superfície da Terra é igual a , desprezando o efeito da latitude, qual deve ser a altura acima da superfície terrestre na qual a aceleração da gravidade é igual a ?
Passo 1
Normalmente o enunciado diz o valor da massa e do raio da Terra, e o valor da constante gravitacional. Pois bem, assumiremos os valores:
Quando estamos a uma distância da superfície da terra a aceleração da gravidade será .
Com isto, para achar a distância acima da superfície da Terra basta assumirmos um crescimento do raio:
Passo 2
Agora, vamos fazer as contas!
Botando o em evidencia no denominador, temos:
Mas sabemos que , é a gravidade no superfície da Terra, então
Agora temos que isolar . Pra isso vamos primeiro multiplicar cruzado
Aí vamos tirar a raiz quadrada dos dois lados
Substituindo os valores, vamos ter o seguinte
Show de bolinhas! :D
Resposta
Exercício Resolvido #5
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 397 ex. 7
Na superfície da Lua, a aceleração da gravidade vale . A uma distância do centro da Lua igual a quatro vezes o raio da Lua, a aceleração da gravidade vale:
- Nenhuma dessas respostas
Passo 1
Sabemos que a fórmula que temos que usar para encontrar a aceleração da gravidade é:
Portanto, pelo enunciado, temos:
E para encontrar o que queremos, temos que usar que:
E então:
Simplificando:
Resposta
Letra d
Exercício Resolvido #6
Elaboração própria
Você foi contratado por uma agência espacial para estudar sobre um novo planeta recém descoberto, e sua primeira função é calcular a gravidade na superfície do planeta. Já é conhecida sua massa de e seu raio de . De acordo com seus cálculos, qual é o valor da gravidade em questão?
Dado:
Passo 1
O primeiro passo é ficar muito feliz! Ser contratado para trabalhar numa agência espacial é de um reconhecimento ímpar! E uma conta bancária par, né rs.
Passo 2
Vamos lá, já nos foi dado a massa, o raio e a constante gravitacional. Podemos aplicar diretamente na fórmula da gravidade na superfície de um planeta qualquer, mas vamos deduzí-la mais uma vez para você nunca mais esquecer.
Para dar uma lembrada, primeiro usamos a força convencional de atração de um corpo, a força peso.
Em seguida, usamos a força gravitacional de atração de um corpo.
E como elas são a mesma força calculada de forma diferente, basta igualá-las.
Passo 3
Pronto, agora podemos substituir os valores dados na questão:
Resposta
Exercício Resolvido #7
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 401 ex. 63
Uma partícula pontual de massa está sobre o eixo em e uma partícula idêntica está sobre o eixo em . (a) Qual é a orientação do campo gravitacional da origem? (b) Qual é a magnitude deste campo?
Passo 1
A gente precisa calcular o campo gravitacional aqui, já que o problema nos pede a orientação e a magnitude dele em relação a origem O, na nossa língua quer dizer que ele quer o valor do campo e pra onde ele aponta. Temos duas partículas idênticas que tem a mesma distância da origem.
Vamos desenhar o problema:
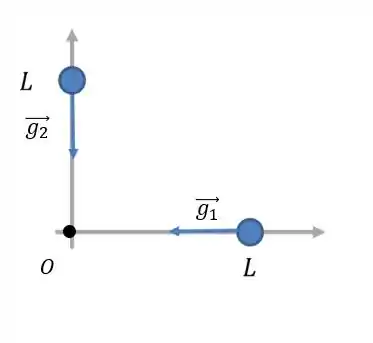
Repara que a gravidade pra cada uma das partículas aponta pra um sentido diferente. O campo gravitacional depende da massa e também da distância quanto mais distante menor é a influencia do campo e nesse caso todas as componentes são iguais pra cada partícula. Vetorialmente falando a fórmula que descreve o campo gravitacional é essa aqui:
Passo 2
Quando ele fala em orientação a gente pode pensar em duas coisas, na orientação vetorial ou no ângulo da resultante desse campo. A gente viu como funciona na fórmula e só vamos precisar ali mudar o sentido, que é negativo.
E pra encontrar o ângulo dessa resultante a gente pode desenhar a resultante dos vetores e calcular a tangente do triângulo.
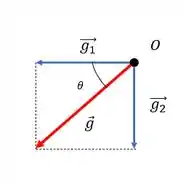
Que vai ser dada por cada módulo aqui, já que os vetores ortogonais possuem só uma direção:
E aí a gente faz a inversa:
Passo 3
E o módulo do vetor é só fazer o Pitágoras daquele mesmo triângulo com as compontenes em módulo, se liga:
Substituindo geral a gente tem:
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física II – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 27
Duas esferas uniformes, cada uma com massa igual a , estão fixas nos pontos e . Determine o módulo, a direção e o sentido da aceleração inicial de uma esfera uniforme com massa quando ela é liberada do repouso no ponto e sofrendo apenas atrações gravitacionais das esferas situadas em e .
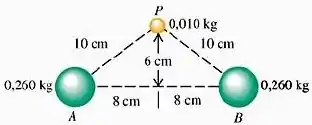
Passo 1
A massa da esfera que está no ponto não vai interferir, porque? Lembra que a aceleração da gravidade é
Basta assumirmos sendo a distância entre as esferas, e sendo a massa da esfera verde e pronto temos as acelerações do ponto . Pois bem, assumiremos os valores:
Como os corpos tem a mesma massa a intensidade da gravidade é igual, vamos calcular?
Passo 2
As acelerações vão ser assim
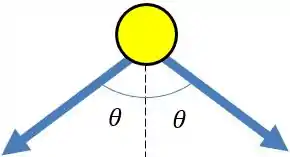
Repara que os ângulos são iguais porque os triângulos são iguais. Como as acelerações são iguais vamos ter apenas componente vertical, ambas apontando para baixo. Usando a “regra do COlado/SEparado” vamos ter
Mas quem é cosseno de ? Olha no triângulo da figura inicial, o cosseno não é cateto adjacente sobre hipotenusa? Então
Vamos ter
Passo 3
Essa é a COMPONENTE de cada gravidade a aceleração total vai ser
Resposta
Exercício Resolvido #9
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 401 ex. 64
Cinco corpos, cada um de massa , estão igualmente espaçados sobre um arco de semicírculo de raio , como na Figura 11-25. Um corpo de massa está localizado no centro de curvatura do arco. (a) Se é , é e é , qual é a força gravitacional sobre a partícula de massa devida aos cinco corpos? (b) Se o corpo de massa é removido, qual é o campo gravitacional no centro de curvatura do arco?
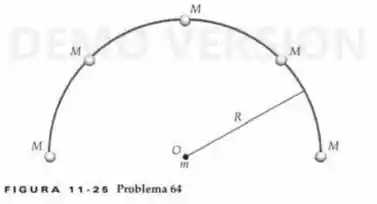
Passo 1
a) Sabemos que para encontrarmos o a força gravitacional resultante, basta somarmos vetorialmente todas as forças exercidas na massa . Se liga na figura:
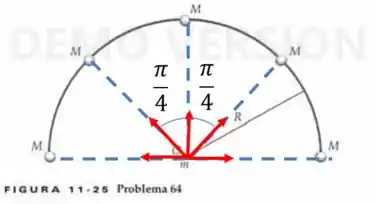
Percebe-se que todas as componentes horizontais se anulam, portanto:
Onde é a força gravitacional entre uma massa e a massa , logo:
Substituindo os valores:
Passo 2
b) Para achar o campo gravitacional, nós aprendemos a fazer o seguinte:
Portanto, o campo gravitacional NÃO DEPENDE da massa .
Então, concluímos que, podemos manter o mesmo vetor encontrado para a força, divindo-o somente pelo valor da massa :
Resposta
Exercício Resolvido #10
UNICAMP-P1-2012-Q2
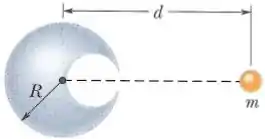
Uma esfera de chumbo de raio possui uma cavidade esférica cuja superfície passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera, antes de a cavidade ser aberta, era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros da esfera e da cavidade?
.
Passo 1
Vamos primeiramente calcular a força que a esfera de chumbo faz na esfera menor, sem ter a cavidade.
Passo 2
Agora vamos imaginar a cavidade como sendo uma esfera de raio , cujo o centro de massa está a uma distância de da esfera pequena. Agora vamos calcular a força gravitacional que essa cavidade esférica exerceria na esfera pequena.
Entretanto, não temos a massa dessa cavidade esférica. Mas podemos descobrir utilizando a fórmula da densidade:
Para a esfera sem a cavidade, temos que e o volume será:
Logo, substituindo:
Agora é só utilizar a densidade para a cavidade:
Entretanto, ainda temos que calcular o volume da cavidade. Mas sabemos que o raio da cavidade é a metade do raio da esfera, ou seja, é .
Substituindo na fórmula:
Agora é só substituir na fórmula
Passo 3
Agora para calcular a força que a esfera com a cavidade faz, é só diminuir as duas forças: