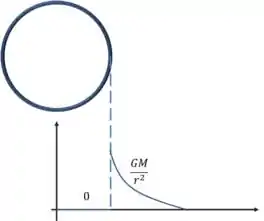
Aceleração da gravidade no interior de cascas e esferas
Produzido por Ludovic BeghinTeoria
Até agora aprendemos como calcular o campo gravitacional gerado por corpos maciços, certo? Mas e se tivéssemos somente uma casca de massa? Como ela agiria na criação de um campo gravitacional?
Vamos analisar dois casos: o do campo gravitacional dentro e fora de uma casca esférica, ou seja, para e , respectivamente.
Campo gravitacional dentro da casca esférica()
Vamos primeiramente considerar o ponto como centro da casca esférica .
Vamos traçar os campos gerados por alguns “caquinhos” de mesma massa (são os pontinhos verdes espalhados de forma simétrica na superfície da casca) no seu centro.
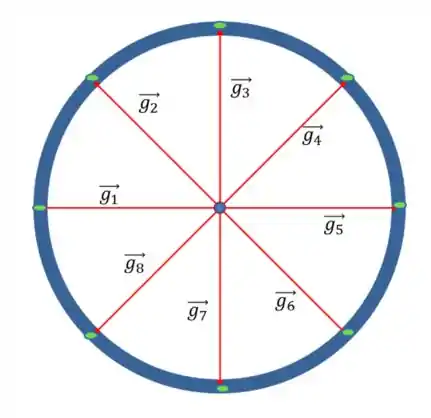
Viu só? Todos os campos têm o mesmo módulo e estão dispostos de forma que o campo resultante no centro seja nulo:
A simetria esférica da casca nos garante que isso irá ocorrer quando considerarmos todos os caquinhos presentes na superfície! Ou seja, quando , sempre teremos:
Campo gravitacional fora da casca esférica()
Assim como na efera maciça, a casca esférica nos permite fazer o acúmulo da massa no centro da casca, portanto, quando , teremos:
Onde é a massa total da casca.
Também ainda não calculamos o campo gravitacional dentro de uma esfera maciça. Podemos ver isso agora, topa? Então bora lá!
Campo gravitacional no interior de uma esfera maciça()
Quando queremos calcular o campo com , é só a gente considerar a massa que está dentro dessa esfera de raio . Vamos chamar essa massa de .
Como a esfera é homogênea, podemos garantir que:
Portanto, o campo é:
Substituindo o valor de :
Podemos então resumir tudo com dois gráficos:
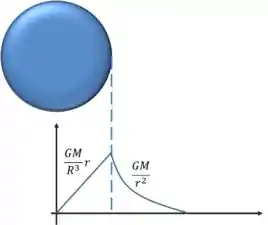
Show de bola? Bora praticar!
Campo gravitacional fora da casca esférica( r > R )
Campo gravitacional no interior de uma esfera maciça( r < R )
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 398 ex. 15
Explique por que o campo gravitacional dentro de uma esfera maciça de massa homogênea é diretamente proporcional a e não inversamente proporcional a .
Passo 1
Quando queremos calcular o campo com , é só a gente considerar a massa que está dentro dessa esfera de raio . Vamos chamar essa massa de .
Como a esfera é homogênea, podemos garantir que:
Portanto, o campo é:
Substituindo o valor de :
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 397 ex. 8
A uma profundidade igual à metada do raio da Terra, a aceleração da gravidade vale cerca de:
- Não se pode determinar a resposta com os dados fornecidos
Passo 1
Sabemos que a fórmula que nos dá a aceleração da gravidade dentro da esfera, a uma distância do centro é:
Quando a profundidade é , temos que a distância do ponto considerado ao centro é:
No enunciado, nos foi dado que:
E então:
Substitituindo:
Como a aceleração da gravidade na superfície, , é dada por:
Conclui-se que:
Resposta
Letra C
Exercício Resolvido #3
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 401 ex. 70
Uma casca esférica fina e homogênea tem de raio e de massa, e seu centro está localizado na origem de um sistema de coordenadas. Outra casca esférica fina e homogênea, com de raio e de massa, está dentro da casca maior, com seu centro em no eixo . Qual é a força gravitacional de atração entre as duas cascas?
Passo 1
O campo gravitacional dentro da casca de é nulo e, portanto, a força gravitacional também é nula.
Pela 3ª lei de Newton, concluímos que a casca interna também não exerce força sobre a casca externa.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 401 ex. 73
Duas cascas esféricas finas, homogêneas e concêntricas, possuem massas e e raios e , como na Figura 11-26. Qual é a magnitude da força gravitacional sobre uma partícula pontual de massa (não mostrada) localizada (a) a uma distância do centro das cascas? (b) a uma distância do centro das cascas? (c) a uma distância do centro das cascas?
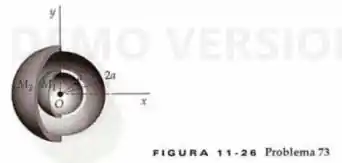
Passo 1
a) Como a distância é maior que os raios das duas cascas, podemos acumular a massa no centro das duas cascas e então:
Passo 2
b) À distância de , estamos dentro da casca maior e fora da casca menor, certo? Portanto, a casca maior NÃO exercerá força sobre a massa , mas a casca menor, podemos acumular a massa no centro da mesma. Se liga então:
Passo 3
c) Já à distância de , estamos dentro das duas cascas, portanto, o campo gravitacional é nulo e, portanto, a força gravitacional também é nula.
Resposta
Exercício Resolvido #5
Hugh D. Young e Roger A. Freedman, Física II – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, p. 29 ex. 38
Uma casca esférica, uniforme, de massa igual a , possui um raio de . (a) Ache a força gravitacional que essa casca exerce sobre uma massa pontual de colocada nas seguintes distâncias do centro da casca: (i) , (ii) , (iii) . (b) Desenhe um gráfico qualitativo do módulo da força gravitacional que essa esfera exerce sobre uma massa pontual em função da distância de do centro da esfera. Inclua a região de a .
Passo 1
a)
(i) Para distâncias maiores que o raio da casca, basta acumular a massa no centro da casca:
Passo 2
(ii) Como a distância é menor que o raio da casca:
Passo 3
(iii) Novamente, como a distância é menor que o raio:
Passo 4
b)
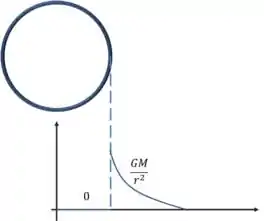
Resposta