Força e Campo Gravitacional Envolvendo Integrais
Teoria
Show de bolinhas galerinha, até agora vimos exemplos e exercícios de corpos com simetria esférica sobre efeito da força gravitacional.
No entanto, diversas distribuições contínuas de massa são capazes de também criar um campo gravitacional e é exatamente essas expressões que regem as forças geradas por este campo que iremos estudar.
Para entender melhor o jeito da coisa, nada melhor do que um exemplozinho.
Exemplo
Vamos imaginar uma linha de massas de massa total e tamanho , disposta sobre um eixo como na figura abaixo:
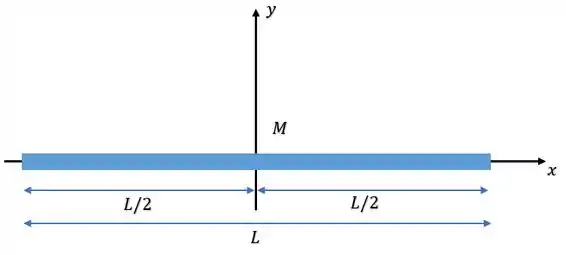
Vamos encontrar o campo gravitacional resultante, sobre um ponto que está uma distância sobre o eixo :
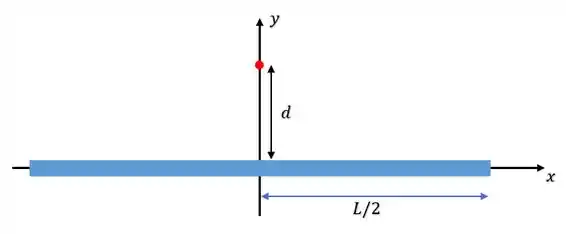
Nesse caso, teremos que cada pedacinho bem pequenininho de massa da nossa linha, vai exercer uma atração gravitacional igualmente pequena sobre o ponto:
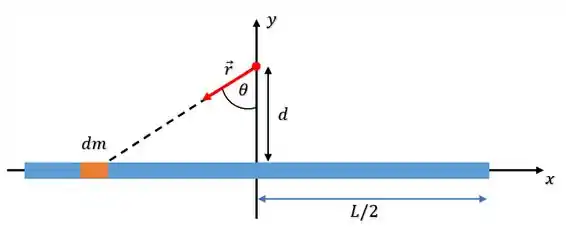
Onde representa a versor unitário da direção da atração gravitacional que a massa exerce sobre o ponto.
Dessa maneira, o campo gravitacional gerado pela linha, sobre o ponto, será resultado da soma de todas as atrações gravitacionais que todas as massas exercem sobre esse ponto. Ou seja, como temos uma soma de infinitas atrações , podemos aplicar os conceitos de integral para calcular o campo gravitacional resultante , tal que:
Como a aceleração gravitacional é medida através da equação:
A atração de uma massa , será:
Lembrando que esse representa somente a direção que aponta o campo. Mas beleza, essa nossa direção possui componentes em dois eixos, então isso quer dizer que podemos decompor ela em suas coordenadas, saca só, vamos ter que:
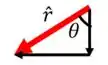
Sendo assim, podemos expressar a direção como:
Como é o vetor unitário , então , de forma que:
Assim a nossa integral se divide em duas:
Tal que:
Mas calma ai chefia, porque nem tudo está perdido. Pra facilitar nossas contas, podemos usar a simetria do problema a nosso favor, se liga só, a mesma massa que existe de um lado do eixo, existe simetricamente do outro, isso quer dizer que a atração gravitacional que elas exercem nesse eixo, se encontram de uma maneira que:
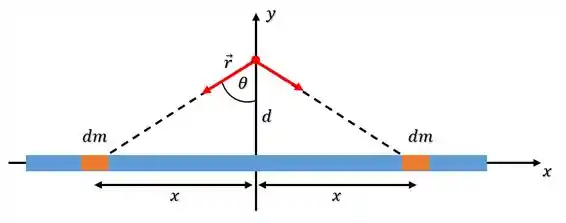
A malandragem disso tudo, é que as forças horizontais que as massas exercem sobre o ponto, se anulam com as forças que as outras massas exercem em posições simétricas:
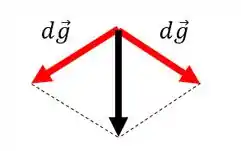
Isso quer dizer que componente horizontal do compo gravitacional será nula, e a resultante do campo gravitacional vai possuir resultante somente no eixo . Logo:
Agora o nosso problema é que não conhecemos aquele pedacinho de massa . Mas pra isso podemos usar o fato da massa ser distribuída continuamente, isso quer dizer que a densidade linear vai ser igual em qualquer ponto do corpo. Então pra uma massa que tem um comprimento :
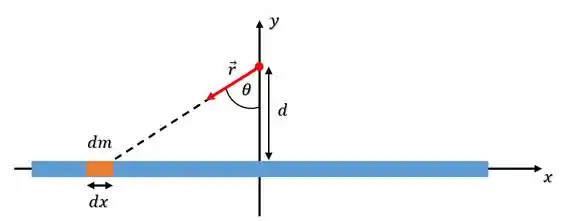
Teremos uma densidade linear dada como:
Como a barra é homogênea, podemos encontrar essa tal de densidade linear usando a massa total e o comprimento total , tal que::
E então, encontrar a relação de com :
Logo:
Belezoca, e susbituindo isso na nossa integral, obtemos que:
Outra coisa que podemos reparar, é que a nossa variável agora passou a ser o , e nesse caso temos que a barra varia no eixo de até , afinal colocamos seu centro bem no meio do eixo. Logo os limites de integração serão e :
Agora temos que deixar tudo em função de ! Olhando de novo pra nossa figura, temos um triângulo retângulo dando sopa aqui
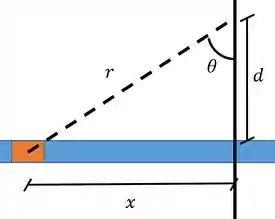
Desse triângulo a gente tira que:
Além disso, também conseguimos tirars as relações trigonométricas:
Substituindo no nosso campo, obtemos que:
Agora.... agora não tem muito pra onde a gente fugir! Temos que lidar com essa belezinha aí! Mas não grila muito não, porque essas integrais de raízes sempre são tabeladas e já vêem prontinhas pra gente. É exatamente dessa água que a gente bebereis, se liga só nessa integralzinha tabelada aqui:
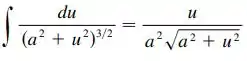
Igualzinha a nossa né não!? Só gente trocar o pelo e o pelo . Isso quer dizer que nossa integral será:
Então se a gente substituir os limites de integração, vamos obter que:
E o nosso campo vai ser dado por:
Dessa maneira, o módulo do campo gravitacional , será:
E pra finalizar, o sinal negativo em , indica que o sentido da atração é para baixo no eixo .
Um resumo pra isso tudo:
Passo 1: Escrever como uma integral de e separar nas suas componentes
Passo 2: Analisar a simetria do problema e ver ser alguma componente é nula
Passo 3: Escrever o em função de alguma coisa que dê pra integrar. No nosso exemplo
Passo 4: Ajeitar os limites de integração, achar relações pra escrever tudo em função dos dados do problema e da variável de integração.
Passo 5: Meter a cara na integral (dê uma olhada no formulário antes!).
Um pouco trabalhoso, né? Mas com a prática você vai dominar isso aí. Bora praticar pra você ficar craque nisso!
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP-P1-2007- Q2
A figura abaixo representa um anel delgado de raio e massa homogênea e uma massa pontual que está situada no eixo que passa pelo centro do anel a uma distância do mesmo. Dois elementos infinitesimais de massa do anel, diametralmente opostos, são ilustrados na figura.
(a) Calcule o módulo da força resultante gravitacional infinitesimal que atua sobre a massa pontual devido à presença das massas infinitesimais .
(b) Qual é o módulo da força gravitacional resultante sofrida pela massa pontual devido, agora, à presença de todo o anel?
(c) Obtenha o módulo da força gravitacional para e para .
Passo 1
(a)
Pela lei de Newton da Gravitação Universal cada massa exercerá uma força
As componentes das forças se somam e as demais se cancelam. Então:
Passo 2
(b)
Como o anel é homogêneo:
Onde é o comprimento de arco da massa . Assim, substituindo na equação do item anterior, temos:
Passo 3
(c)
Já temos o módulo de . Basta substituir o valor da distância até o centro do anel.
Para , temos que .
E para , vamos ter
Resposta
a)
b)
c)
Exercício Resolvido #2
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 403 ex. 101
Determine a magnitude do campo gravitacional a uma distância de uma barra fina e homogênea de comprimento infinito, cuja massa por unidade de comprimento é .
Passo 1
Vamos desenhar o problema usando inicialmente uma barra de tamanho , depois de encontrar a expressão, a gente tende o pra infinito, beleza?
Como vamos integrar caminhando pelo eixo , precisamos de uma relação entre os infinitesimais de massa e de posição. Como a massa é homogênea e nos foi dado a densidade linear:
Passo 2
Essa massa vai exercer um campo no nosso ponto que está a uma distância da barra
Onde é o unitário apontando na direção de para o ponto em que estamos interessados.
Passo 3
Para cada pedaço da barra a esquerda do nosso ponto vamos ter um pedaço a direita. Se somarmos a contribuição de campo que cada pedaço faz vamos ter um campo na direção vertical como na figura abaixo!
Assim o nosso campo resultante aponta na direção ! Então para pegar a componente temos que multiplicar o nosso campo por
Passo 4
Pela figura conseguimos ver um triângulo retângulo com catetos e e hipotenusa , assim
E também conseguimos calcular o cosseno de
Juntando tudo isso finalmente temos
Agora só falta integrar esse troço!
Passo 5
Sabemos que, para encontrar a magnitude do campo integral total da barra, vamos integrar o campo gerado por cada caquinho de massa:
Essa integral fica mamão com açúcar fazendo a substituição
Quando , temos que e quando , temos que
Derivando dos dois lados, temos
Substituindo o lá na integral, e mudando o intervalo de integração
Vamos focar nessa integral aqui
Lá embaixo no denominador, vamos colocar o em evidência
Aí agora a gente tem que usar aquela relação trigonométrica SUPER ÓBVIA (#sqn)
Aí a nossa integralzinha fica
Lembra o que é secante?!?!? É isso aqui ó
De forma que aquela integral monstra vira isso
Agora eu faço até com os pés nas costas!
Assim (FINALMENTE)
E voltando pro nosso campo
Como o enunciado pede a magnitude
Resposta
Exercício Resolvido #3
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 403 ex. 65
Uma barra fina e homogênea de , com de comprimento, é dobrada em um semicírculo. Qual é a força gravitacional exercida pela barra sobre uma massa pontual de localizada no centro de curvatura do arco circular?
Passo 1
Vamos desenhar como vai ficar esse semicírculo:
Agora, dá uma olhada nessa barra como um corpo extenso. Cada elemento de massa infinitesimal vai gerar uma força gravitacional infinitesimal na partícula:
Além disso, temos uma simetria no nosso problema. Isso é um ótimo sinal, já que costuma simplificar nossas contas.
Podemos escrever em suas componentes:
E temos que seus módulos serão:
Você já deve estar pensando... que saco ter que calcular cada um desses termos.
Mas aí que a simetria entra em ação para nos ajudar.
Para cada ângulo na nossa figura, vamos ter uma componente apontando para o lado direito e uma componente , de mesmo módulo, apontando para o lado esquerdo.
Logo, elas vão se cancelar, sobrando apenas a componente em para cima:
Passo 2
Agora que temos uma expressão para a força exercida por cada elemento da barra, basta fazer um somatório de todas essas contribuições, ou seja, integrar:
A expressão da força gravitacional é:
No lugar de , chamamos de cada elemento infinitesimal de massa na barra, vamos chamar de a massa da partícula e, por último, temos que a distância entre os dois é sempre . Então:
Retirando as constantes da integral, temos:
Passo 3
Vamos achar algumas relações que nos permitem calcular a integral.
A densidade linear de massa continua a mesma, certo? Então:
Além disso, a densidade linear se relaciona com , da seguinte forma:
Temos também que a nossa barra é um arco de circunferência.
Podemos relacionar arcos e ângulos com:
Sendo o raio da circunferência e o ângulo percorrido pelo arco.
Com isso, podemos descobrir o valor do raio da barra :
Conseguimos também escrever o nosso assim:
Juntando isso tudo, temos que:
Passo 4
Agora, finalmente podemos calcular a integral.
Vamos substituir , lembrando dos limites de integração de que varrem de a , ou seja, de a :
Arrumando a casa:
Vamos resolver essa integral, rapidamente:
Chegamos, então, que:
Substituindo os valores, temos:
Para finalizar, resta lembrar que a direção do vetor força gravitacional resultante é em para cima.
Resposta
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física II – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, p. 34 ex. 89
A massa está uniformemente distribuída ao longo de um disco de raio . Determine o módulo, a direção e o sentido da força gravitacional entre o disco e a partícula de massa localizada a uma distância acima do centro do disco (Figura 12-39). O seu resultado se reduz a uma expressão correta quando assume valores muito elevados? (Sugestão: Divida o disco em anéis finos concêntricos infinitesimais; a seguir, integre o resultado para achar a força total.)
Passo 1
Beleza, esse problema é um pouco grandinho, mas vamos por partes que vai dar tudo certo.
Primeiramente vamos encontrar o campo gravitacional gerado por um anel fino de raio e massa . Desenhando vamos ter isso aqui:
O que acontece é que pra cada pedacinho de massa do anel tem um outro pedacinho do outro lado e quando a gente soma a força gravitacional desses dois, a força resultante tem que apontar para baixo.
Isso significa que ao somarmos todas as contribuições de cada pedacinho do anel, a força total irá apontar para baixo também. Esse raciocínio é o que a gente chama de argumento de simetria!
Como a nossa força resultante aponta para baixo, na hora de somar todas as contribuições vamos levar em consideração somente a componente vertical. Assim, olhando a geometria do nosso problema, pra projetar cada força na direção vertical a gente tem que multiplicar pelo cosseno de . Pela nossa figura
Passo 2
Outra coisa importante é que todos os pontos com massa desse anel estão à mesma distância r da massa , assim a força exercida por cada pedacinho vai ser
Mas como nos importa a componente vertical então temos que calcular
Aí agora temos que integrar esse cara pra calcular a força total
Nós vamos integrar todos os pedacinhos do anel agora, ou seja, só . Como , , e são os mesmos pra todos os pedaços então são constantes na nossa integral, o que permite que a gente faça
E o que é essa integral de ? É somente a massa total do nosso anel! Assim a força gravitacional exercida pelo anel será
Passo 3
Agora que já sabemos a força gravitacional para um anel genérico, temos que ajustar essa expressão encontrada para chegar na força exercida por um disco. Esse disco é composto por vários anéis e o raio desses anéis vai variar de até (raio do disco).
Pra isso então teremos que fazer uma nova integral que vai ser algo do tipo
Mas como ligar o anel com o disco? Bem, se eu disse que o que varia de um anel pro outro é o raio então temos que ter no final uma integral em !
Pra isso tem o pulo do gato que é olhar pra massa de cada anel! A densidade de massa de todos os anéis é igual, concorda? Eles são feitos do mesmo material! O que muda de um pro outro é o raio, e consequentemente o seu comprimento. Assim anéis maiores vão ter mais massa! Vamos usar essa informação então
Agora eu vou supor que um dado anel vai ter um raio e uma espessura beeeemm pequenina de forma que a sua área vai ser o seu comprimento vezes essa espessura
Qual vai ser a massa desse anel? Ela vai ser agora um
Esse é a densidade superficial de massa do disco! Se sabemos que o disco tem massa e área , então essa densidade superficial de massa é
Assim, a massa do anel será
No fundo nós fizemos essa regra de 3
Passo 4
Finalmente estamos prontos pra montar a nossa última (eu prometo!) integral
Já calculamos a força de anel um anel de massa
Como estamos falando de um anel de massa então vamos mudar para
Substituindo o do passo anterior
Jogando isso na nossa integral finalmente ficamos com
Finalmente temos uma integral com !!!!!!
Agora, vamos lá! Os limites de integração são de até e como a integral é em podemos tirar da integral tudo que é constante, assim
Passo 5
Agora é só fazer essa integralzinha aí rsrsrsrsrs
Você pode olhar no nosso material de cálculo onde tá tudo super explicadinho aqui! Eu vou fazer aqui, mas lá tem mais detalhes se você quiser dar uma relembrada, belezinha?
Essa integral é feita por substituição. Pra isso vamos definir uma nova variável pra sumir com esse do denominador, assim
De forma que (lembrando que é constante aqui!)
E os limites de integração ficam
Assim a nossa integral fica
Passo 6
Pronto! Agora é só jogar na nossa expressão da força!
Supondo , vamos ter , assim
Botando o fora do parênteses pra dentro
Show! Achamos a expressão pra força exercida pelo disco! Agora só falta botar a direção! Chamando de direção para baixo teremos
Passo 7
Agora vamos ver se essa expressão faz sentido quando assume valores muito elevados. O que significa isso? Isso significa tomar o limite de indo pra infinito! Pra isso vamos olhar a parte que contém na nossa expressão, ou seja, vamos olhar para o seguinte limite
Pra fazer esse cara vamos reescrever a raiz como
(Supondo )
Assim o nosso limite será
Então a nossa expressão pra força exercida pelo disco será
Ou seja, láááááá no infinito a força exercida pelo disco vai ser nula, o que faz total sentido já que quando a gente tiver infinitamente afastado de um corpo a influência dele será nula! ;)
Resposta
Essa expressão vai para no limite o que é o esperado quando dois corpos estão infinitamente afastados.
Exercício Resolvido #5
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 403 ex. 104
Uma esfera homogênea de massa está localizada próximo a uma barra fina e homogênea de massa e comprimento , como na Figura 11-31. Determine a força gravitacional de atração exercida pela esfera sobre a barra.
Passo 1
Começamos aqui usando a simetria da esfera para acumular toda a sua massa em seu centro, criando forças que variam somente com o inverso do quadrado da distância.
Se liga na imagem:
A expressão para será:
Como a barra é homogênea:
E a relação entre e é dada por:
Passo 2
Então, para encontrarmos a força total, basta integrarmos:
Logo:
Sabemos a direção e o sentido da força: