As massas e coordenadas de três esferas são as seguintes: , , ; , , ; , , . Qual é o módulo da força gravitacional que as três esferas exercem sobre uma esfera de 20 kg localizada na origem?

Vamos começar calculando as distâncias de cada esfera até a origem, usando o teorema de Pitágoras:

Agora que temos as distâncias podemos calcular os módulos das forças, e depois usar um pouco de trigonometria para achar as componentes em cada direção ( e ).

A fórmula para a força gravitacional entre dois corpos é:

Portanto as forças entre a esfera da origem e cada uma das outras três:

Agora vamos decompor essas forças nas direções e , depois estaremos prontos para somá-las e terminar a questão. Em cada caso, é só multiplicar a distância da esfera à origem pelo cosseno do ângulo entre o eixo e o vetor.

Vamos lembrar que a força gravitacional é atrativa, e precisamos ajustar os sinais de acordo com isso (imagem fora de escala):

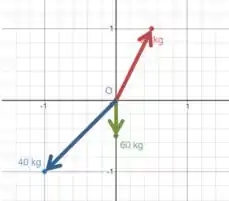
Decompondo a seta vermelha:

Decompondo a seta azul:

Decompondo a seta verde:

Agora vamos somar as componentes em cada direção:

E o módulo da força resultante vai ser:

Pronto!