Velocidade de Escape e Rotação da Terra
Produzido por Ludovic BeghinTeoria
Quando fizemos o cálculo da velocidade de escape da Terra, encontramos a seguinte expressão:
Mas tem um porém. Quando fizemos este cálculo, não consideramos o movimento de rotação da Terra.
“Mas que saco! Tudo tem que complicar!”
Calma, querido aluno, isso é sinal de que você está evoluindo no estudo da Física, inserindo cada vez mais detalhes e se aproximando da realidade. =D
Agora vamos devagar e rapidinho tu vai entender.
Antes de tudo: você lembra o que é o movimento de rotação da Terra? Isso mesmo! É o movimento onde a terra gira em torno do seu próprio eixo. Este é o movimento que marca um dia terrestre, ou seja:
Agora precisamos saber como esse movimento influencia na velocidade de um corpo que tenta sair da terra. Se liga na imagem:
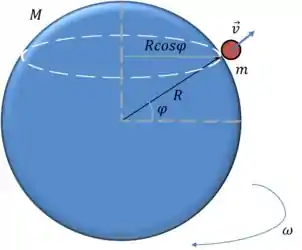
Com a imagem conseguimos encontrar a velocidade que está sendo adicionada ao corpo de massa devido ao movimento de rotação da Terra.
O ângulo é chamado de latitude e é sempre medido a partir da linha do Equador.
A velocidade angular pode, como sempre ser substituída por:
E então:
E a velocidade de escape corrigida tem a seguinte expressão:
Tranquilo?
Essa teoria só complementa o que já vimos lá na velocidade de escape, mas é importante que você saiba a definição do ângulo de latitude e como este movimento de rotação da Terra influencia nos corpos na superfície.
Bora praticar!
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física II – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 30
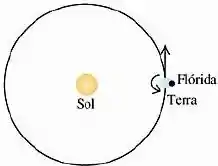
Desejamos lançar uma espaçonave da superfície da Terra de modo que ela também escape do sistema solar. a) Calcule a velocidade relativa ao centro da Terra com a qual ela deve ser lançada. Considere os efeitos gravitacionais do Sol e da Terra e inclua o efeito da velocidade orbital da Terra, mas despreze a resistência do ar. b) A rotação da Terra pode auxiliar a atingir esta velocidade de escape. Calcule a velocidade que a espaçonave deve possuir em relação à superfície da Terra se a espaçonave for lançada da Flórida no ponto indicado na figura abaixo. A rotação da Terra em torno do seu eixo e seu movimento orbital em torno do Sol possuem o mesmo sentido de rotação. Em Cabo Canaveral um lançamento ocorre na latitude de
ao norte do equador. c) A European Space Agency (ESA) utiliza uma plataforma de lançamento na Guiana Francesa (imediatamente ao norte do Brasil), situada a ao norte do equador. Com que velocidade em relação à superfície da Terra deve uma espaçonave ser lançada da plataforma de lançamento na Guiana Francesa para que ela escape do sistema solar?
Passo 1
Vamos pensar juntos. O foguete vai pra bem longe do Sol, certo? Então a força gravitacional vai ser baixíssima, tendendo a zero. Sendo assim, a forma de calcular essa velocidade fica sendo a partir da energia, cujo valor é zero no infinito.
É fácil pensar desse jeito. É só analisar o enunciado, se o corpo está “fugindo” do Sol, velocidade calculada por energia. Se o corpo está do ladinho do Sol fielmente, velocidade calculada pela força resultante de rotação.
Passo 2
a)
Que comecemos os trabalhos com a conservação da energia.
A energia inicial vai ser a energia gravitacional da Terra mais a energia gravitacional do Sol mais a energia cinética resultado da velocidade.
Lembrando que é o raio da Terra e é o raio da orbita terrestre.
Dando aquela consultada no Google vemos que
Além disso
Como ele está na Terra e a terra está se movendo.
Passo 3
Repara que temos um detalhe a levar em consideração aqui, a translação da Terra.
Essa velocidade que achamos é a velocidade total, mas ele já possui uma velocidade inicial que é a da translação da terra, precisamos então subtrair essa velocidade. Primeiro vamos acha-la
Sabemos o tempo que a Terra demora pra dar uma volta ao redor do Sol, e sabemos o percurso então
Onde
Então
Passo 4
A velocidade de escape então vai ser
Passo 5
b)
Agora estamos levando em consideração a rotação da Terra também, então a velocidade vai ser um pouco menor de novo. Precisamos achar a velocidade de rotação da Terra e subtrair na velocidade que achamos no item a
Onde
Cuidado com um detalhe, ele não está no equador, está em um ponto com ângulo , a velocidade precisa ser corrigida, seria
Ele sai da Flórida então.
Encontramos então
Passo 6
A velocidade de escape vai ser
Passo 7
c)
Dessa vez ele sai da Guiana francesa então a velocidade de rotação ali vai ser
Encontramos então
Passo 8
A velocidade de escape vai ser