Exercícios de Velocidade de escape e rotação da Terra - Lista de Exercícios Resolvida

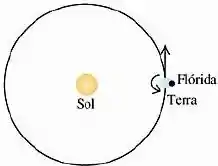
Desejamos lançar uma espaçonave da superfície da Terra de modo que ela também escape do sistema solar. a) Calcule a velocidade relativa ao centro da Terra com a qual ela deve ser lançada. Considere os efeitos gravitacionais do Sol e da Terra e inclua o efeito da velocidade orbital da Terra, mas despreze a resistência do ar. b) A rotação da Terra pode auxiliar a atingir esta velocidade de escape. Calcule a velocidade que a espaçonave deve possuir em relação à superfície da Terra se a espaçonave for lançada da Flórida no ponto indicado na figura abaixo. A rotação da Terra em torno do seu eixo e seu movimento orbital em torno do Sol possuem o mesmo sentido de rotação. Em Cabo Canaveral um lançamento ocorre na latitude de

ao norte do equador. c) A European Space Agency (ESA) utiliza uma plataforma de lançamento na Guiana Francesa (imediatamente ao norte do Brasil), situada a ao norte do equador. Com que velocidade em relação à superfície da Terra deve uma espaçonave ser lançada da plataforma de lançamento na Guiana Francesa para que ela escape do sistema solar?

Um satélite de massa m orbita um planeta de massa M e raio R em uma órbita de altura 2R acima da superfície do planeta. A energia mínima requerida para mudar o satélite para uma órbita na qual a altura do satélite é de 3R acima da superfície do planeta é:

a) GMm/(24R)

b) GMm/(15R)

c) GMm/(48R)

d) 2GMm/(21R)

e) 3GMm/(5R)

Marque a afirmação errada:

a) Em módulo, a força gravitacional com a qual o Sol atrai a Terra é a mesma força com a qual a Terra atrai o Sol.

b) A aceleração gravitacional no interior de uma casca esférica uniforme isolada é nula, independentemente de sua massa.

c) Segundo a teoria Newtoniana, a velocidade de escape de um corpo não depende de sua massa.

d) A 2a lei de Kepler (lei das áreas) é consequência direta do fato de que o momento angular dos planetas é conservado.

e) A rotação da Terra em torno de si torna a aceleração de queda no Equador da Terra maior que nos polos.

f) A 2a lei de Kepler nos permite concluir que a velocidade da Terra é menor quando ela está mais distante do Sol (Afélio).