Força de Atrito
Produzido por Ludovic BeghinTeoria
O que é o Atrito?
O que faz um armário não sair do lugar quando empurramos ele sem tanta força? Ou o que nos faz conseguir andar com o movimento de “empurrar o chão pra trás”? A força de atrito é responsável por esses dois fenômenos, e muitos outros que você ainda vai ver. Ela aparece quando há contato entre superfícies que não são perfeitamente polidas, ou seja, em qualquer situação real, já que o conceito de ideal ou perfeito, é somente aqui, no papel.
A força de atrito tem a característica de se opor ao movimento, como nos dois exemplos citados acima e ilustrados abaixo.
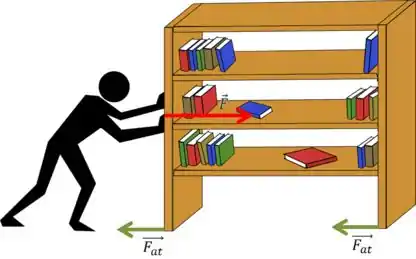
Aqui, a entre o armário e o chão agem contra a força aplicada, impedindo do armário se mover.
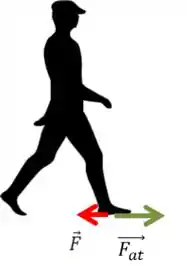
Já aqui, o atrito entre o pé e o chão nos “joga” pra frente, quanto tentamos empurrar o chão pra trás. Sabemos como é difícil andar no gelo por exemplo, ou em uma pista de boliche, que são superfícies muito polidas e que, portanto, possuem o atrito muito pequeno com o pé.
Cálculo da aceleração e do atrito em sistemas com blocos
Uma outra situação bem comum nos exercícios são blocos apoiados um no outro, vamos ver um exemplo pra gente entender melhor, imagine o esquema abaixo sabendo que , e , qual vai ser a aceleração dos blocos? Explique também o motivo do bloco não se mover pro lado oposto.
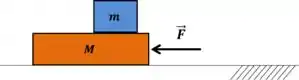
Nesse exemplo, só existe atrito entre as superfícies dos dois blocos. Se nada for falado sobre um bloco se deslocar na direção oposta do outro, a gente pode considerar que os dois blocos formam um sistema e possuem a mesma aceleração!
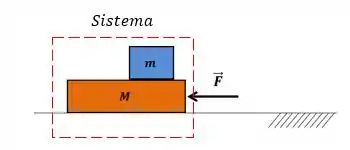
E aqui é o seguinte se esse sistema anda junto, a massa dele é a soma da massa dos blocos e sendo assim a nossa segunda lei de Newton vai ficar:
E aqui a aceleração do sistema é igual a de cada bloco, então isolando encontramos o que foi pedido:
E se a gente substituir nossos valores teremos:
E há uma coisa interessante acontecendo. A força está agindo somente no bloco de maneira direta. Se ambos os blocos estão com a mesma aceleração, que força está fazendo o bloco ter essa aceleração? Aqui vale a gente fazer um diagrama de corpo livre pra analisarmos o que rola no bloco m.
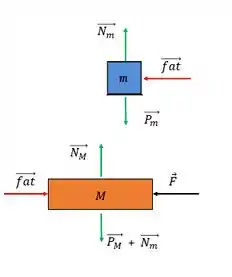
Como vimos, a força de atrito age no sentido contrário do movimento, e como o movimento natural do bloco seria manter a sua inércia e deslizar para a direita do bloco , a força de atrito faz o seu trabalho e arrasta o bloco , e como é a única força na horizontal pela segunda lei de Newton a gente vê que:
Daí substituindo os valores encontrados, temos:
E aqui tem mais um detalhe, como o bloco não escorrega sobre o bloco a força de atrito é estática, se por acaso o bloco deslizasse a força de atrito seria dinâmica, porém esse tema a gente vai ver melhor depois, nos próximos tópicos.