Polias Móveis
Produzido por Ludovic BeghinTeoria
Fala aí! Vamos agora estudar um pouquinho mais a fundo as polias móveis e entender a grande novidade que elas trazem em relação às polias fixas.
Antes disso, vale falar que tem alguns conceitos iniciais que preciso que você esteja dominando antes de prosseguirmos aqui, beleza? Se precisar dar uma revisada, saca só essa listinha que separei pra você 🤩
O que são polias móveis?
As polias móveis são aquelas que estão livres para se movimentar na corda ou cabo de tração. Diferentemente das polias fixas, elas não se encontram presas ao teto ou parede. Dá só uma olhada nessa ilustração mostrando os dois tipos:
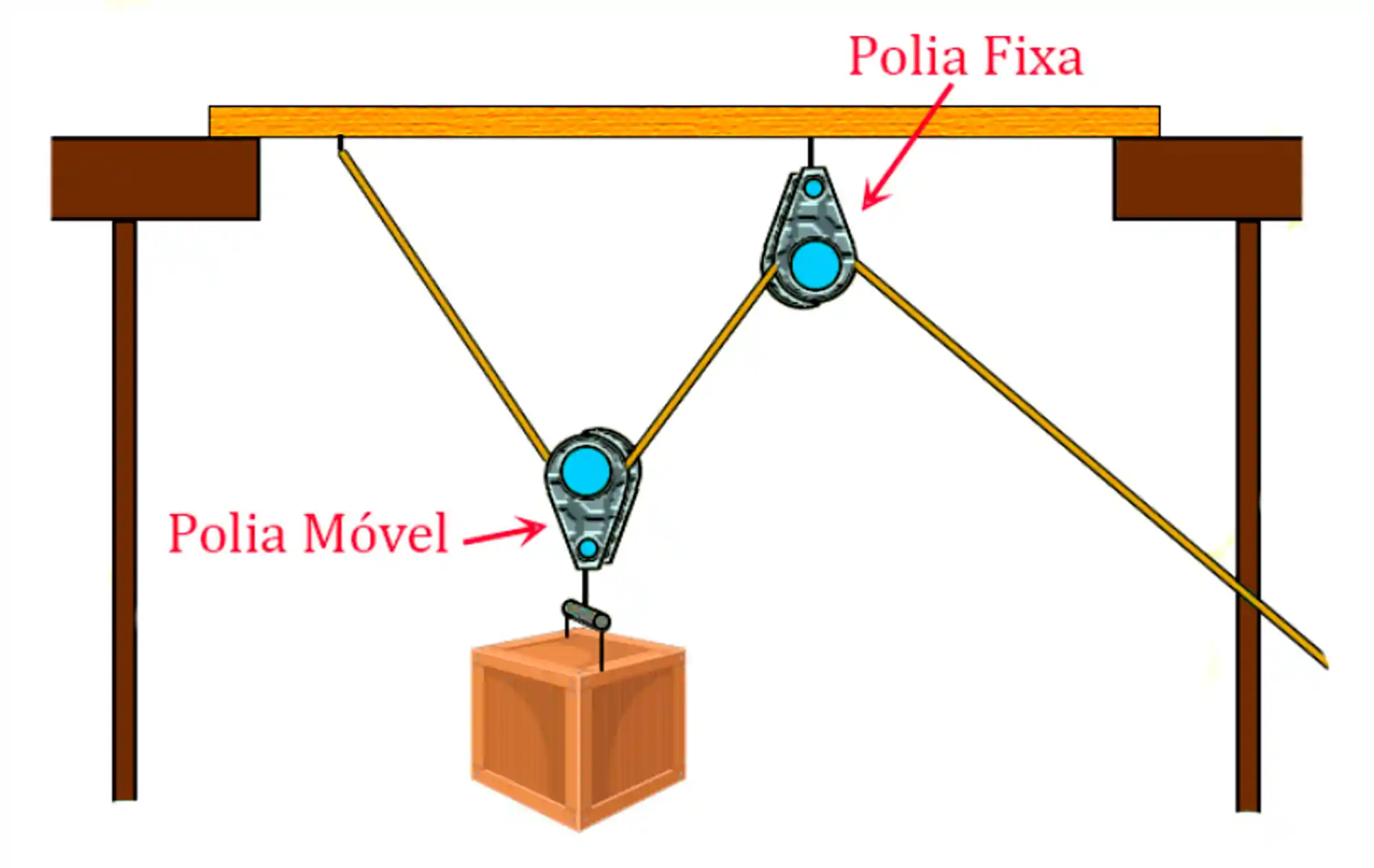
Apesar dessa diferença entre os dois tipos de polias parecer bem simples, ela traz funcionalidades completamente revolucionárias. Enquanto as polias fixas só redirecionam a aplicação da força, as polias móveis são capazes de reduzir pela metade a força necessária para levantar um objeto!
E esse efeito acumula para cada polia móvel introduzida no sistema!
Incrível, né? Podemos até generalizar uma fórmula para a força que deverá ser exercida para levantar um objeto com base no número de polias móveis.
Essa força
Quer dizer que se a gente tiver um sistema como esse aqui:

Com um total de três polias móveis, qual deve ser o valor de
Bora aplicar naquela fórmula? Com
Precisamos exercer somente
Percebe o tanto que as polias móveis podem ser úteis no nosso dia a dia?
Bora ver como funciona isso na aplicação em sistemas com um ou mais objetos.
Polia móvel com um bloco
Vamos aplicar esses conceitos que acabamos de aprender um pouquinho mais detalhadamente no seguinte exemplo.
Exemplo: Calcule a aceleração do sistema abaixo se uma força de 100 N é aplicada para levantar o bloco de massa
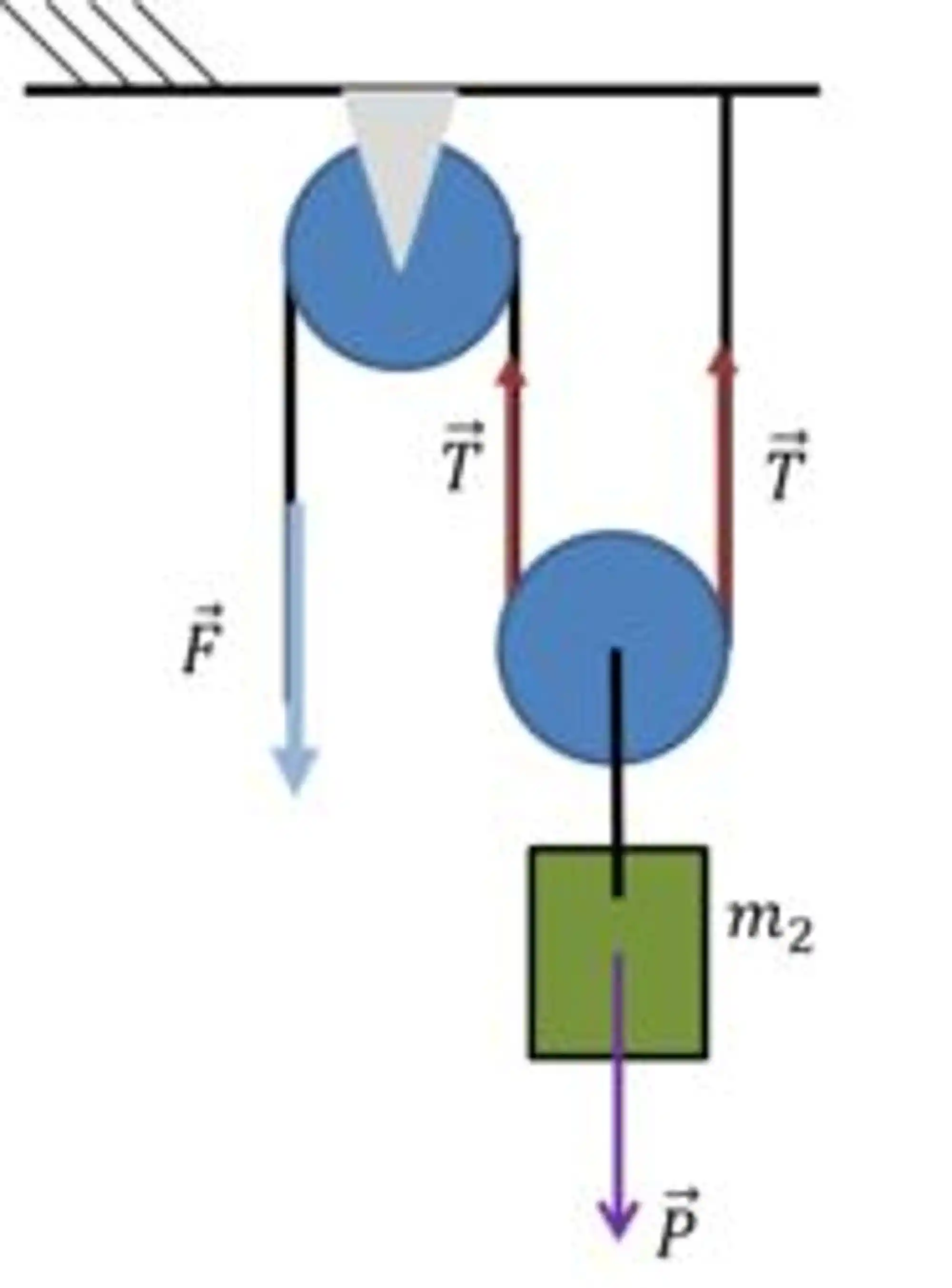
Temos sempre que ter em mente dois conceitos:
- A tensão é a mesma em todo o comprimento do fio;
- Os fios estão sempre tensionados e são inextensíveis.
A partir destes conceitos, podemos chegar na seguinte equivalência ali na extremidade em que a força é aplicada:
Já para a polia móvel, vamos montar um diagrama de corpo livre e analisar o que tá rolando ali.
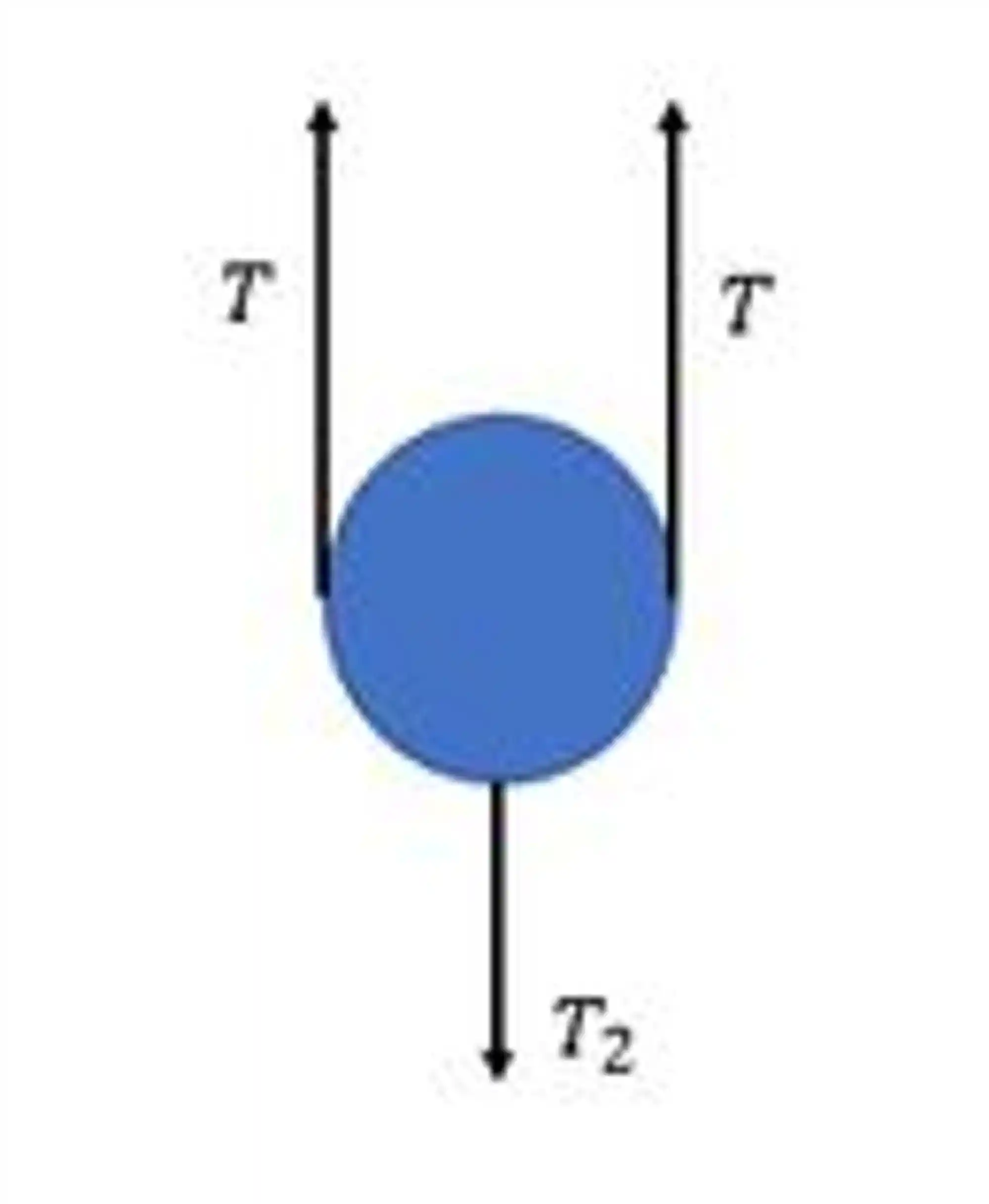
Considerando o equilíbrio da polia móvel, precisamos que tudo o que aponta para cima seja igual ao que aponta para baixo.
Como já sabemos que
Com isso em mente, podemos fazer o diagrama de corpo livre para o bloco.
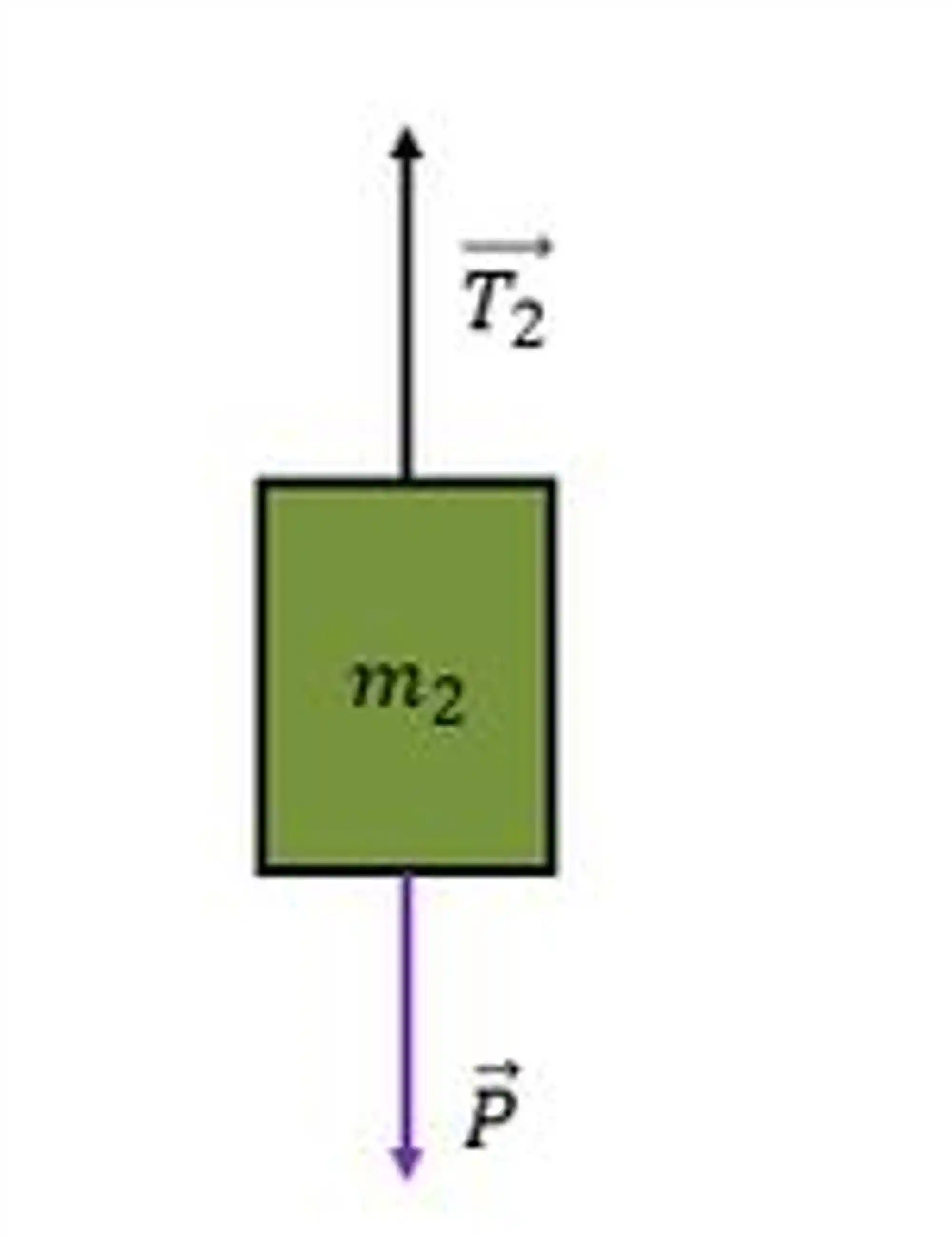
Chegamos que a força resultante nesse bloco é, adotando o referencial para cima positivo:
Mas, lembra que a segunda lei de Newton nos diz que a força resultante é o produto da massa pela aceleração? Então podemos escrever o seguinte:
Se isolarmos a aceleração, ficamos assim:
E aí é só substituir os valores e resolver, lembrando que
Tranquilo, né? E se a gente tivesse mais de uma polia móvel no sistema, seria só seguir o que fizemos aqui: montar o diagrama de corpo livre para cada uma e fazer a correspondência das forças.
Então bora complicar só um pouquinho mais.
Polias móveis com mais de um bloco
E se agora a gente tivesse uma situação parecida com essa aqui:
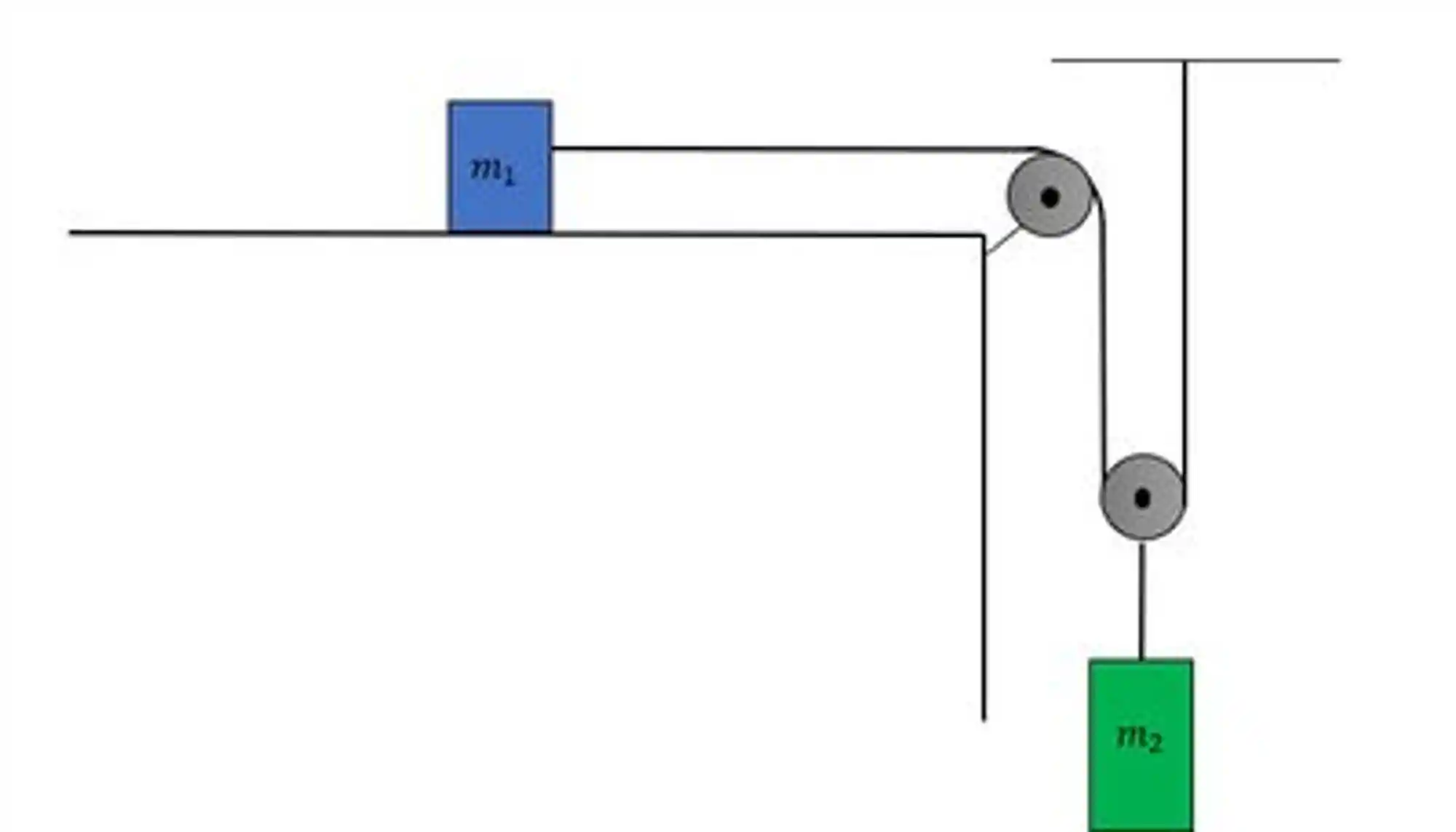
Se o bloco azul possui massa
Bora começar com o diagrama de corpo livre do bloco azul:
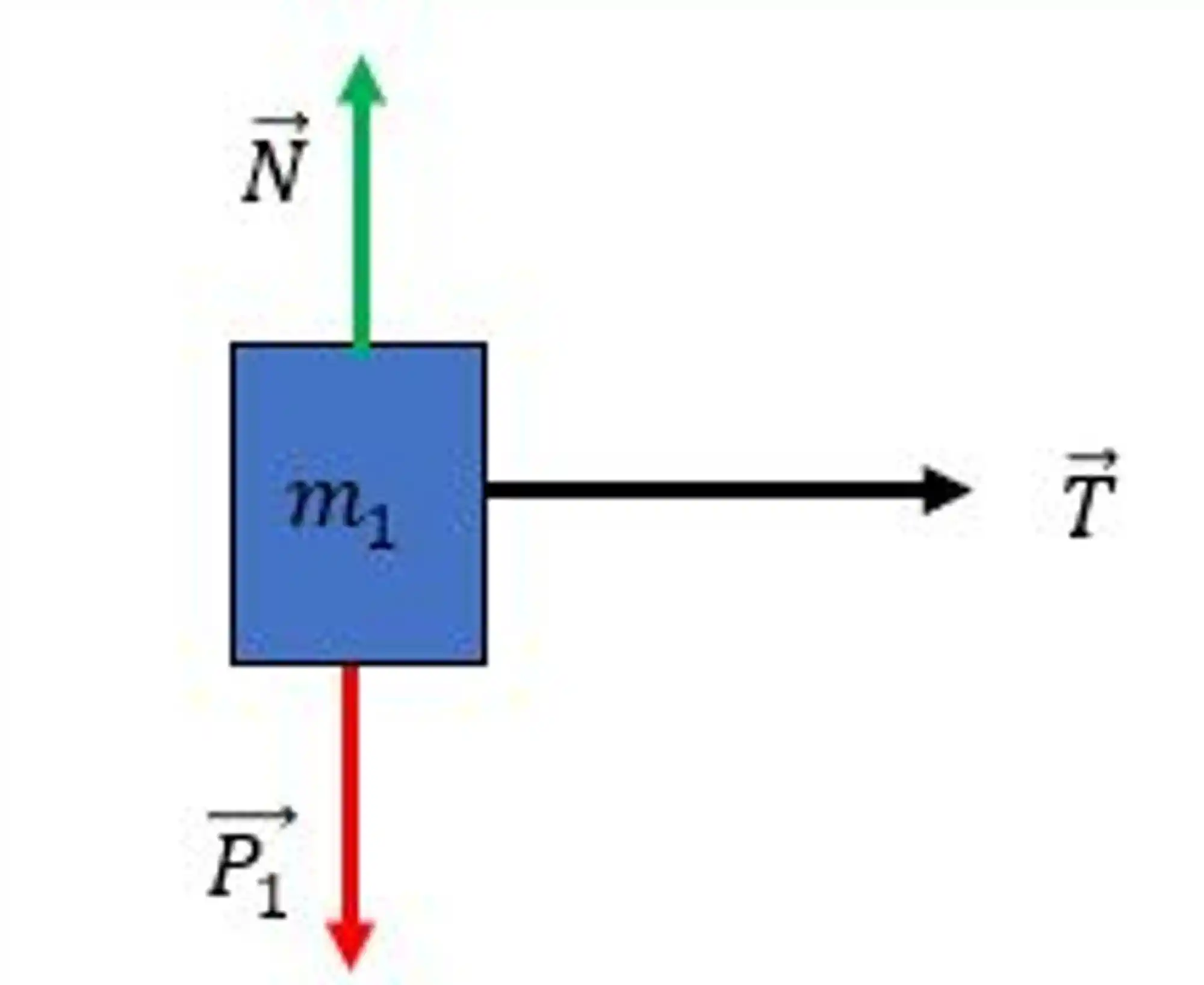
Percebe que a resultante vai ser só aquele
Então, da segunda lei de Newton, vamos ter:
Como a polia fixa só vai redirecionar a força, não precisamos fazer nenhuma análise nela.
Bora para a polia móvel:
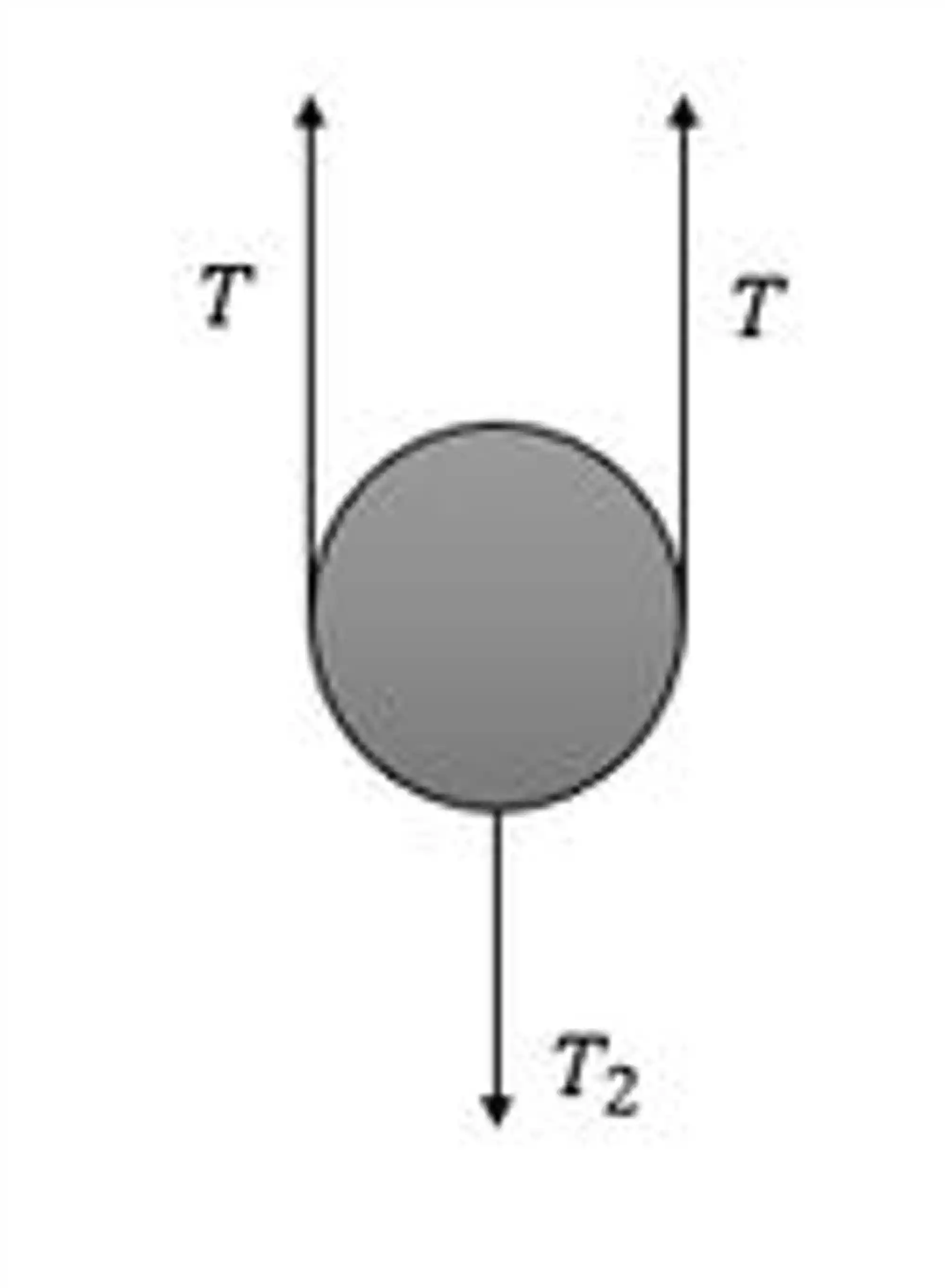
Daqui, a gente tira que:
E, para o bloco verde:
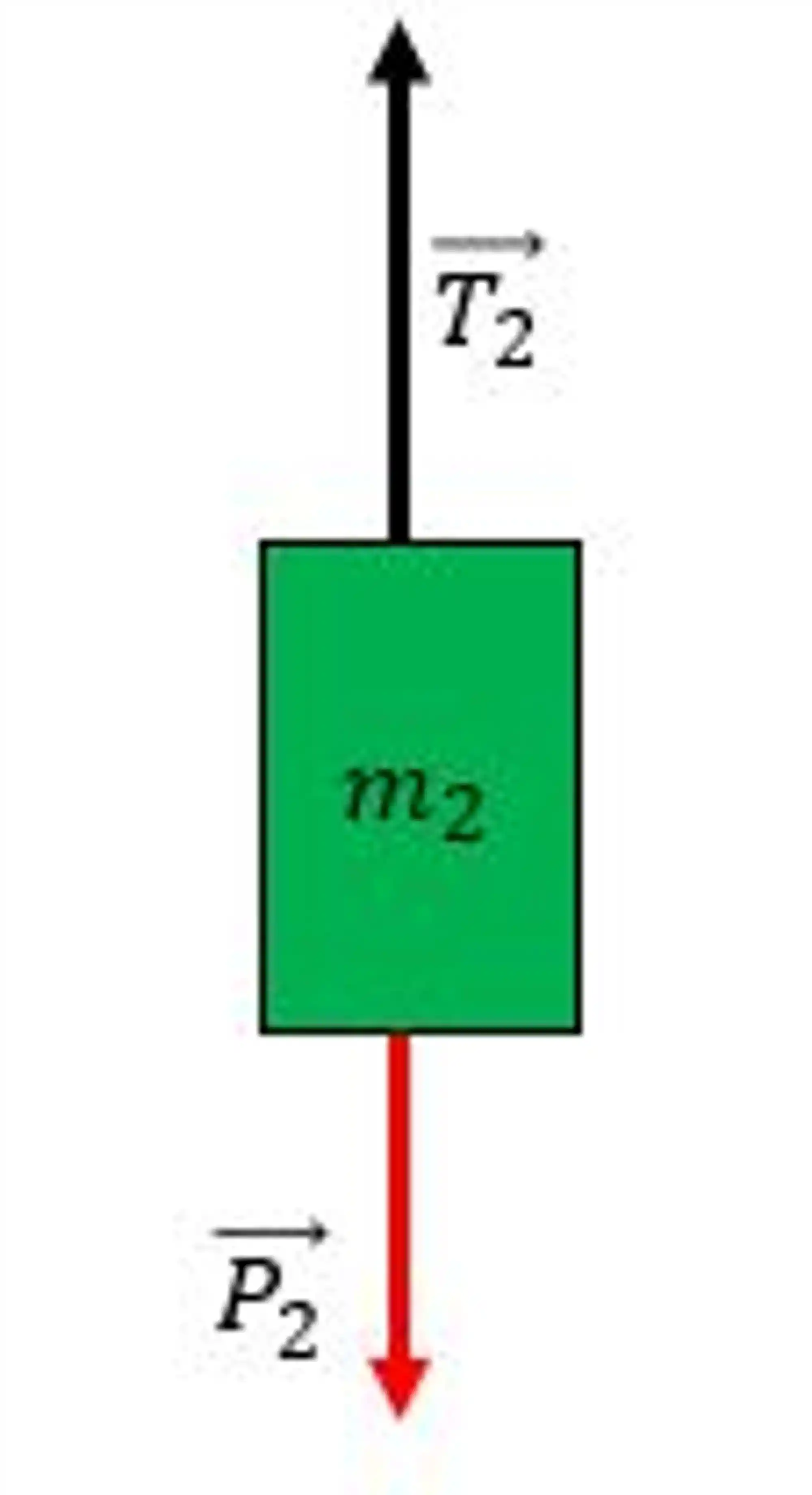
Aplicando a segunda lei de Newton:
E, como o
Mas lá do bloco azul, descobrimos que
Queremos encontrar o valor de
Agora é só substituir os valores e resolver para
Tá aí a nossa resposta, sem segredos! Bora praticar com mais algumas variações desses exercícios para ficarmos craques.
Polia móvel com um bloco
Polias móveis com mais de um bloco
Exercícios Resolvidos
Exercício Resolvido #1
USP- P1-2011-Q4
Na figura abaixo tem-se uma massa que está conectada a uma massa através das polias e que tem massas despreziveis. Supondo que a massa desliza sobre a mesa sem atrito e que a aceleração da massa é vertical e para baixo, pede-se:
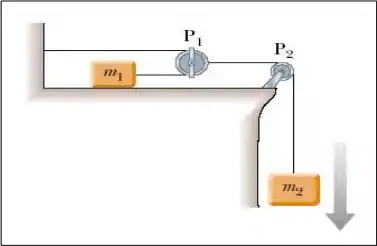
(a) Coloque em um diagrama todas as forças que atuam no sistema.
(b) Determinar o valor numérico da razão , considerando os fios inextensíveis.
(c) Determinar as trações e em função de , e .
(d) Determinar as acelerações e .
Passo 1
a)
As forças que atuam no sistema estão representadas na figura abaixo, onde corresponde a força de apoio da polia que anula a resultante das forças que atuam nessa polia e geram uma resultante no sentido oposto de .
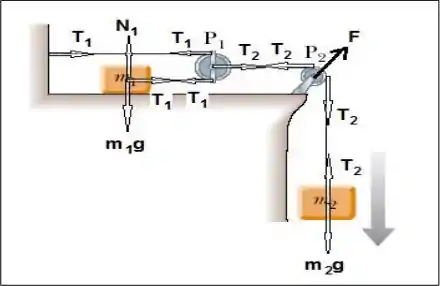
Passo 2
b)
Devido a polia não fixa que liga o bloco de massa ser conectada por 3 fios, quando a massa se deslocar de um comprimento a massa se deslocará de um comprimento . Portanto, como o bloco terá que percorrer o dobro da distância no mesmo tempo, a aceleração dele terá que ser o dobro. Então, , logo:
Passo 3
c)
Vamos primeiramente escrever as equações de movimentos para os três corpos que possuem aceleração diferente de zero que são as massas e e a polia .
Devido a massa das polias serem desprezíveis, da equação vamos ter:
Substituindo isso na equação obtemos:
Substituindo a aceleração que encontramos no item :
Da equação temos que:
Substituindo isso:
Logo vale:
E vale 2 vezes o , ou seja:
Passo 4
d)
Basta utilizar a equação do item anterior e substituir o valor da tração:
E
Resposta
a)
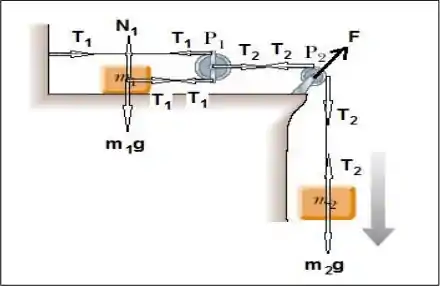
b)
c)
d)
Exercício Resolvido #2
PUCRIO-P1-B-2012.2 Q3
Considere o mecanismo apresentado na figura, onde o bloco 1 está apoiado em uma superfície sem atrito e o bloco 2 está sustentado por uma polia móvel sem massa (corpo 3 na figura). A polia fixa é ideal. O fio (ideal) conecta o bloco 1 à polia móvel e está fixo ao teto. O fio (ideal) sustenta o bloco 2 à polia 3.
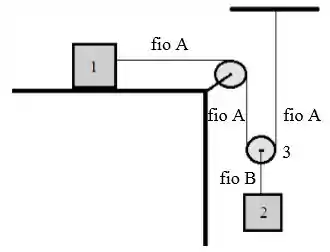
Neste mecanismo, devido ao vínculo existente entre o fio e a polia móvel, o módulo da aceleração do bloco 1, é o dobro do módulo da aceleração do bloco 2, .
As massas dos blocos são e . A massa da polia móvel . Use .
a) Represente os diagramas de corpo livre para os blocos 1 e 2 e para a polia móvel 3, explicitando todas as forças que atuam neles.
b) Escolha sistemas de coordenadas adequados para cada corpo (explicite-os!) e escreva as equações literais (não substitua ainda os valores das massas ou !) resultantes das leis de Newton para os três corpos.
c) A partir das equações do item obtenha literalmente e então substitua os valores fornecidos para encontrar o valor numérico do módulo de .
d) Obtenha o módulo da tração exercida pelo fio sobre o bloco 2.
Passo 1
a)
Basta representar as forças em cada corpo: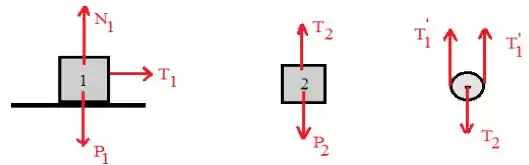
Passo 2
b)
O bloco 1 só tem movimento para a direita, enquanto o bloco 2 e a polia tem movimento vertical para baixo. Assim, pelo acoplamento dos dois movimentos, vamos definir para o bloco 1 o eixo positivo para a esquerda e para o bloco 2 e polia, definimos o eixo positivo para baixo.
Para o corpo 1:
Para o corpo 2:
Para a polia móvel:
Passo 3
c)
Foi dado que (equação de vínculo) (5)
Por outro lado, como as polias são não massivas e o fio 1 inextensível, o módulo de é igual ao módulo de
Usando estas informações, ficamos com as seguintes equações:
Se somamos temos:
Passo 4
d)
Da equação :
Temos:
Daí:
Resposta
a)
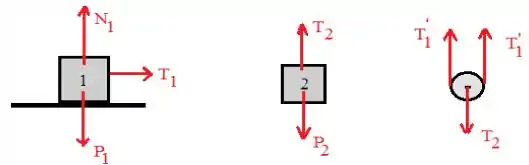
b)
Para o corpo 1:
Para o corpo 2:
Para a polia móvel:
c)
d)
Exercício Resolvido #3
USP- P1-2014-Q4
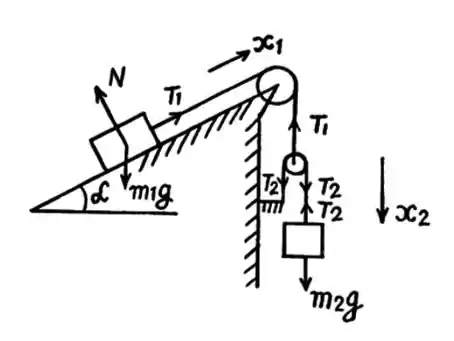
Considere o sistema com plano inclinado envolvendo polias esquematizado na figura abaixo. Não considere atrito. Assuma também que a massa das polias e dos fios são desprezíveis em comparação às massas e dos blocos e , respectivamente. Além disso, os fios não se esticam ou se deformam em geral. Note que a polia que sustenta o bloco está conectada ao fio ligado ao bloco e, assim, essa polia não está fixa.
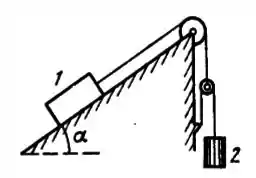
Esboce o diagrama das forças envolvidas, escreva a relação entre as diferentes tensões nos fios, e expresse a Segunda Lei de Newton para cada caso.
Demonstre a relação entre a aceleração do bloco e a aceleração do bloco .
Encontre o valor do ângulo no qual muda de sinal.
Obtenha a expressão geral para
Calcule o valor nos limites: e .
Passo 1
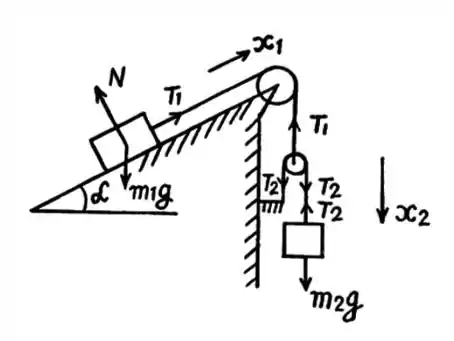
Como assumimos que a massa da polia pequena é nula, a força resultante sobre ela é nula e assim ela dividirá igualmente a força entre os dois fios. Portanto, vemos que .
As forças resultantes em cada corpo são:
Passo 2
Bom, vamos imaginar que o corpo suba uma distância , sendo . Como os fios estão conectados e sempre esticados, o corpo descerá uma distância , sendo .
Muito bem, agora é importante ter bastante atenção e imaginação ao observar a figura. Como os fios estão conectados e esticados, quando o corpo subir uma distância , a polia menor obrigatoriamente descerá uma distância .
Quando a polia menor descer uma distância , o corpo descerá uma distância , visto que seu ponto de apoio é a polia menor, se seu ponto de apoio descer, você desce junto. Mas, o fio apoiado na parte esquerda da polia menor não poderá descer essa distância , justamente por estar preso em um suporte. O que acontecerá então? Bem, a distância que o lado esquerdo do fio não desceu será transferido ao lado direito! Girando a polia menor e jogando mais fio do lado direito. Dessa forma, em vez de descer uma distância , o corpo descerá uma distância .
Logo, temos finalmente que:
Passo 3
A aceleração muda de sinal quando passa pelo zero. Assim, fazemos nas equações do item :
Agora a segunda equação:
Lembrando que , Logo:
Igualando essas expressões encontramos:
Passo 4
Usando que e , manipulamos as expressões para as forças resultantes para mostrar diretamente que:
Substituindo na segunda equação:
Ficando com o sistema:
Multiplicando a segunda equação por :
Somando as equações ficamos com:
Dividindo o numerador e denominador por , ficamos com:
Passo 5
Utilizando a expressão do item anterior, vamos começar com que é o mais fácil:
Agora para analisar , precisamos fazer isso aparecer na expressão. Então vamos multiplicar o numerador e denominador por :
Logo:
Resposta
Exercício Resolvido #4
PUCRIO-P1-B-2014.1 Q2 letras a e b
Considere as polias e as cordas ideais para o dispositivo da figura abaixo. Despreze suas massas e o atrito das cordas com as polias. Como a polia que sustenta o bloco 2 é móvel, o módulo da aceleração do bloco 1 equivale ao dobro do módulo da aceleração do bloco 2. Adote os valores para as massas dos blocos e . A inclinação do plano é . Não há atrito entre o bloco 1 e o seu plano de apoio. Utilize .
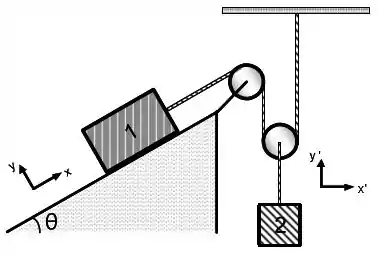
a) Represente o diagrama do corpo livre e escreva as equações de movimento em termos de suas componentes para os dois blocos e a polia móvel presa ao bloco 2. Utilize os sistemas de coordenadas fornecidos para cada componente do sistema.
b) Calcule o vetor aceleração de cada um dos blocos, usando como referência o sistema de coordenadas convencional apresentado para o bloco 2.
Passo 1
a)
Temos o seguinte diagrama:
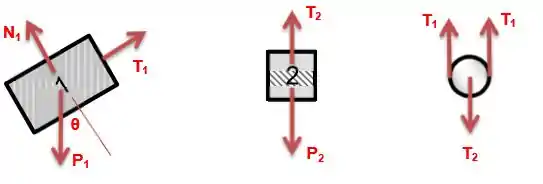
Para o bloco 1:
Eixo :
Eixo :
Para o bloco 2:
Eixo :
Para a polia:
Eixo :
Passo 2
b)
Da equação temos e por causa da roldana móvel: e .
Multiplicando a equação por 2 e substituindo a equação na equação temos:
Somando a equação e a equação temos que:
As acelerações no sistema de coordenadas solicitado são:
Resposta
a)
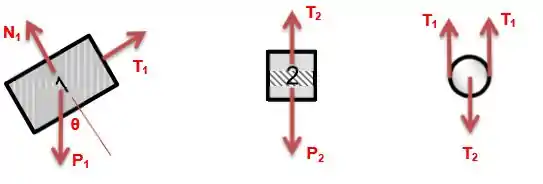
Bloco 1:
Bloco 2:
Polia:
b) ;
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume 2 : gravitação, ondas e termodinâmica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 24-57
A força da Fig. 12-67 mantém o bloco de e as polias em equilíbrio. As polias têm massa e atrito desprezíveis. Calcule a tensão do cabo de cima.
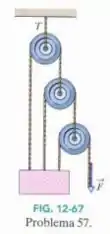
Passo 1
Já aprendemos que:
- A tensão se mantém a mesma no mesmo fio
- Quando o fio dá meia volta em uma polia móvel, essa sofre o dobro da força aplicada em uma de suas extremidades.
Nesse exercício, iremos fazer o diagrama de corpo livre de cada polia e depois aplicar a primeira lei de Newton, já que foi dito que o sistema está em repouso.
Passo 2
Começando da polia mais de baixo, que vamos chamar de Polia 1.
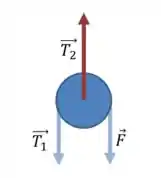
Sabemos que a tensão no fio que envolve essa polia tem que ser a mesma nas duas extremidades, portanto:
E então, como a resultante das forças é nula, temos:
O processo então se repete para a polia do meio, a Polia 2.
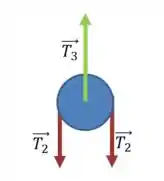
E finalmente, para a Polia 3:
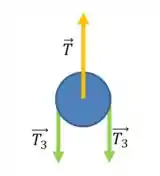
Reunindo as 3 equações obtemos:
Passo 3
Temos que arrumar um jeito agora de descobrir o valor de . Qual informação não usamos ainda? Isso mesmo! Ainda não usamos o fato de que os 3 cabos seguram uma massa dada. Vamos fazer o diagrama do bloco suspenso.
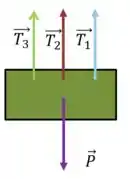
E como o bloco está em repouso:
Substituindo os valores obtidos no Passo 2 e o valor do peso do bloco, temos:
E obtemos então o valor de :
Passo 4
Agora, juntando a relação de com , encontrada no Passo 2, e com o valor de , encontrado no Passo 3, temos: