Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 6.Problemas Adicionais - Ex. 100

100- Um esqui adere à neve quando é deixado em repouso. Quando o esqui se desloca na neve, porém, o atrito o aquece e derrete parcialmente a neve, reduzindo o coeficiente de atrito cinético e facilitando o deslizamento. Encerar o esqui torna-o repelente à água e reduz ainda mais o atrito com a camada de água. Uma loja anuncia que um novo tipo de esqui de plástico é especialmente repelente à água e que, em um declive moderado de 200 m nos Alpes, um esquiador reduziu o tempo de descida de 61 s com esquis convencionais para 42 s com os novos esquis.

Determine o módulo da aceleração média do esquiador

(a) com os esquis convencionais e

(b) com os novos esquis.

Supondo uma inclinação de 3,0°, calcule o coeficiente de atrito cinético

(c) para os esquis convencionais e

(d) para os novos esquis.

Passo 1

a)A aceleração média pode ser tirada da seguinte fórmula, considerando que a velocidade inicial do esqui é de zero.

s = a t 2 2

a = 2 s t 2 = 2 × 200 61 2 = 0.11   m / s 2

b) com os novos esquis temos a mesma fórmula porém com o tempo menor.

a = 2 s t 2 = 2 × 200 42 2 = 0.23   m / s 2

Passo 2

Supondo um esquiador de massa m, o sistema de forças nele será o seguinte.

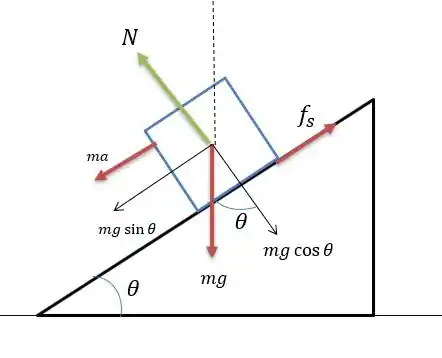
A força resultante na direção paralela a neve vale:

F r = m a = m g sin ⁡ θ - f s

Onde f s é a força de atrito que vale.

f s = μ k N

Onde N vale (pelo equilíbrio das forças perpendiculares a neve).

N = m g cos ⁡ θ

Logo:

m a = m g s i n   θ - μ k m g cos ⁡ θ

Isolando μ k nós teremos:

μ k g c o s   θ = g sin ⁡ θ - a

μ k = g sin ⁡ θ - a g cos ⁡ θ

Passo 3

c) Logo para os esquis convencionais temos que utilizar a aceleração que encontramos para ela no passo 1:

μ k = 9.81 sin ⁡ 3   - 0.11 9.81 cos ⁡ 3 = 0.041

d) Agora para os esquis novos:

μ k = 9.81 sin ⁡ 3 - 0.23 9.81 cos ⁡ 3 = 0.029

Resposta

a )   0.11   m / s 2

b )   0.23   m / s 2

c )   μ k = 0.041

d )   μ k = 0.029

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Processo de trânsito. Você é convocado como testemunha no julgamento de uma violação de trânsito. Os fatos são estes: um motorista freou bruscamente e parou com aceleração constante. Medidas tomadas d
Você faz parte da equipe de projeto para uma exploração do planeta Marte, onde g=3,7m / s 2 . Uma exploradora deve deixar o veículo de exploração que se desloca horizontalmente a 33m / s quando estive
Uma pedra é lançada para baixo sobre a água com velocidade igual a 3m g / k , onde k é o Coeficiente da Equação ( 5.7 ). Supondo que a relação entre a resistência do fluido e a velocidade seja dada pe
Uma rocha com massa m desliza com velocidade inicial v 0 sobre uma superfície horizontal. Uma força retardadora F r que a superfície exerce sobre a rocha é proporcional à raiz quadrada da velocidade i
Um pedaço de rocha com massa de 3,0k g cai a partir do repouso em um meio viscoso. Sobre a rocha atua uma força resultante de cima para baixo de módulo igual a 18,0N (uma combinação entre o peso e a f