Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 13.Problemas Desafiadores - Ex. 100
100. Uma régua uniforme de está suspensa por uma de suas extremidades em um eixo horizontal e oscila como um pêndulo físico. Um objeto muito pequeno com massa igual à da régua pode permanecer preso à régua em um ponto situado a uma distância abaixo do eixo de suspensão. Seja o período do pêndulo com o objeto preso na régua e o período do pêndulo da régua sozinha. Qual é a razão ? Calcule sua expressão para variando de até em intervalos de e faça um gráfico de em função de . Existe algum valor de além de , para o qual ? Caso exista, encontre esse valor e explique por que o período não muda quando atinge esse valor.
Passo 1
Para começar a resolver esse problema, temos que encontrar expressões para e , sabendo que a fórmula do período para o pêndulo físico é:
Agora temos que achar expressões de e para os dois casos em funções dos parâmetros conhecidos e .
Tendo encontrado as expressões para e , basta fazer a razão .
Para responder o item precisamos do gráfico que teremos que fazer no item
Passo 2
Vamos começar achando os parâmetros para o caso que não temos a massa adicionada, então só temos a régua.
Podemos considerar a régua como uma barra, assim o momento de inércia da régua em relação ao eixo que está presa é:
O parâmetro é dado pela distância do centro de massa da régua até o ponto ela está presa, o centro de massa de uma régua é no seu centro, logo:
E a massa da régua é dada pelo enunciado como .
Tendo tudo isso temos que o período é dado por:
Passo 3
A gora vamos achar os parâmetros para o caso que temos a massa adicionada.
Podemos considerar a régua como uma barra, assim o momento de inércia total vai ser a soma do momento de inércia da régua em relação ao eixo que está presa e o momento do objeto em relação ao mesmo eixo.
O momento de inércia da régua é:
E o momento de inércia do objeto, como ele é muito pequeno, é dado por:
Assim, temos:
O parâmetro é dado pela distância do centro de massa da régua mais o objeto até o ponto onde a régua está presa, o centro de massa pode ser calculado da seguinte forma:
Onde é a distância do centro de massa de cada objeto até a origem de referência, que para facilitar nossa vida vai ser onde a régua está presa, então:
Então temos que:
E a massa da régua e do objeto é dada pela soma das massas de cada um que é .
Tendo tudo isso temos que o período é dado por:
Passo 4
Agora que temos uma expressão para e vamos fazer a razão . Então:
Então, temos:
O gráfico dessa expressão é o seguinte:
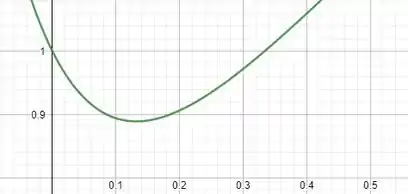
Gráfico:
Passo 5
Agora que temos o gráfico podemos responder o item .
Existe outro ponto além de para que , esse ponto é .
Nesse ponto, um pêndulo simples com comprimento igual a teria o mesmo período que a régua sem o objeto adicionado, os dois corpos oscilariam com o mesmo período e um não afeta o movimento do outro.
Resposta
O ponto é