Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.Problemas Adicionais - Ex. 109

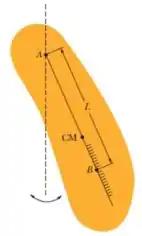
O pêndulo físico da figura tem dois pontos de suspensão possíveis, A e B . O ponto A é fixo, mas o ponto B pode ser deslocado para várias posições, indicadas na figura por uma escala graduada. Quando o pêndulo é suspenso pelo ponto A , o período é T = 1,80   s . O pêndulo é suspenso pelo ponto B e a posição do ponto B é ajustada para que o período seja também de 1,80   s . Qual é a distância L entre os pontos A e B ?

Passo 1

Vamos lembrar da fórmula para o período de um pêndulo físico suspenso por um ponto P :

T P = 2 π   I P m g h P

Sabemos que os pontos A e B tem períodos iguais, então:

T A = T B

2 π   I A m g h A = 2 π   I B m g h B

E nosso objetivo é encontrar a distância entre os pontos, ou seja, L = h B + h A , uma vez que h B e h A são as distâncias dos pontos até o centro de massa (dê uma olhada no desenho).

Passo 2

Vamos simplificar um pouco essa expressão:

I A h A = I B h B

E podemos escrever os momentos de inércia em relação a eixos que passam por A e por B usando o teorema dos eixos paralelos:

I A = I c m + m h A 2

I B = I c m + m h B 2

Então:

I c m + m h A 2 h A = I c m + m h B 2 h B

I c m h B + m h A 2 h B = I c m h A + m h B 2 h A

I c m h B - h A = m h A h B h B - h A

Ou seja:

I c m = m h A h B

Passo 3

Sabemos que o período do pêndulo deve ser T = 1,80   s , então vamos substituir nosso novo resultado em qualquer uma das fórmulas que encontramos no primeiro passo:

1,80 = 2 π   I A m g h A

1,80 = 2 π   m h A h B + m h A 2 m g h A

1,80 = 2 π   h B + h A g

Como vimos no primeiro passo, queremos calcular L = h B + h A , então:

1,80 = 2 π   L g

L = 1,80 2 9,8 2 π 2 = 0,804   m

Resposta

A distância entre os pontos é de 0,804   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pêndulo balístico de madeira, de massa igual a 10k g , suspenso por um fio de 1m de comprimento, é atingido no instante t = 0 por uma bala de 10g , viajando à velocidade de 300m / s , que fica encr
Um pêndulo físico é formado por uma barra delgada homogênea de comprimento l , suspensa por um ponto à distância s (l / 2 ) de seu centro, oscilando num plano vertical. Para que valor de s o período d
Um fio de arame de comprimento 2 l é dobrado ao meio, formando um ângulo de 60 ° , e é suspenso pelo vértice O , oscilando num plano vertical. Calcule o período τ de pequenas oscilações em torno da po
70. Um foguete sobe com aceleração igual a 4,0m / s 2 a partir da plataforma de lançamento na Terra. Dentro do foguete, uma pequena esfera de 1,50k g está pendurada no teto por um fio leve de 1,10m .
71. Um objeto quadrado de massa m é formado de quatro varetas finas idênticas, todas de comprimento L , amarradas juntas. Esse objeto é pendurado em um gancho pelo seu canto superior (Figura 13.37 ).