Exercícios de Pêndulo Físico - Lista de Exercícios Resolvida
Questão 1
Um pêndulo físico de massa e momento de inércia , está preso em uma de suas extremidades. O pêndulo sofre então uma leve perturbação externa, tal que ele começa a oscilar em pequenos ângulos devido a um campo gravitacional . Assuma também que o centro de massa do pêndulo está a uma distância do ponto fixo. Qual a frequência angular de oscilação?
Questão 2
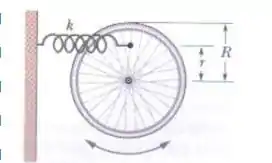
Uma roda pode girar livremente em torno do seu eixo fixo. Uma mola é presa a um dos raios a uma distância de do eixo, como mostra a figura. A roda gira em torno de seu centro.
(a) Supondo que a roda é um disco de massa e o raio , qual é a frequência angular das pequenas oscilações desse sistema em termos de e da constante elástica . Qual é o valor de para :
(b)
(c) ?
Dado:
Momento de inércia de um disco:
Ver solução completaQuestão 3
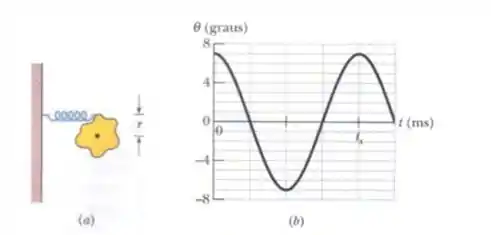
Na Figura abaixo, uma placa de metal está montada em um eixo que passa pelo seu centro de massa. Uma mola com está ligada a uma parede e a um ponto da borda da placa a uma distância do centro de massa. Inicialmente a mola está relaxada. Se a placa é girada de 7° e liberada, oscila em torno do eixo em um MHS, com sua posição angular dada pela a outra figura. A escala do eixo horizontal é definida por . Qual é o momento de inércia da placa em relação ao centro de massa?
Questão 4
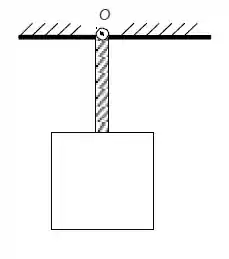
O pêndulo da figura abaixo é formado por uma haste de comprimento e uma chapa quadrada também de lado , presos no ponto de maneira que o conjunto possa se movimentar. Tanto a haste quanto a chapa são uniformes e possuem massa . Os momentos de inércia em torno dos centros de massa de uma haste e de uma chapa quadrada são, respectivamente, e .
- Calcule a distância entre o ponto e o centro de massa desse conjunto .
- Se o pêndulo é posto para oscilar em torno do ponto com ângulo pequeno, qual será o período de oscilação?
Questão 5
Um pêndulo físico é formado por uma régua de um metro, cujo ponto de suspensão é um pequeno furo feito na régua a uma distância da marca de . O período de oscilação é . Determine o valor de
Dados:
Momento de inércia de centro de massa de uma barra:
Ver solução completaQuestão 6
Na figura, o pêndulo é formado por um disco uniforme de raio e de massa preso a uma barra uniforme de comprimento e massa .
- Calcule o momento de inércia em relação ao ponto de suspensão.
- Qual é a distância entre o ponto de suspensão e o centro de massa do pêndulo?
- Calcule o período de oscilação.
Dados:
Momento de inércia de centro de massa de um disco de massa
Momento de inércia de centro de massa de uma barra de massa :
Gravidade:
Ver solução completaQuestão 7
Uma barra homogênea de massa e comprimento é presa por uma de suas extremidades e posta para oscilar como um pêndulo físico sob ação da gravidade . Sabendo que o momento de inércia da barra em relação à sua extremidade é , resolva os itens a seguir:
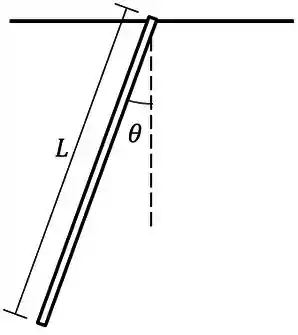
- Deduza a equação de movimento para arbitrário e diga qual a condição (se houver) para o movimento harmônico. Neste caso, qual será a frequência das oscilações?
- Resolva a equação do oscilador harmônico sabendo que o pendulo é inicialmente solto do repouso com ângulo igual a em relação à posição de equilíbrio.
- Adimita agora que haja um torque dissipativo que seja proporcional à velocidade angular, isto é, , onde é uma constante positiva. Escreva a nova equação de movimento e deduza qual deve ser a condição satisfeita por para que haja amortecimento subcritico. Não é necessário resolver esta nova equação de movimento.
Questão 8
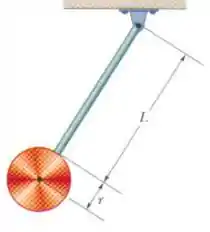
Um pêndulo formado por uma esfera de massa e raio desprezível está suspenso verticalmente a partir do ponto através de uma haste rígida de massa desprezível e comprimento . A haste está ligada a duas molas idênticas de constantes elásticas , massas desprezíveis, situadas a uma distância de como mostrado na figura (a). As molas estão relaxadas (isto é nem esticadas, nem comprimidas) quando o pêndulo está na posição vertical. Para iniciar o balanço do pêndulo, você o desloca com as mãos até que a haste forme um pequeno ângulo com a vertical, liberando-o a partir do repouso [figura (b)].
Dica: como o ângulo é pequeno, considere que as molas permanecem essencialmente na horizontal durante todo o movimento.
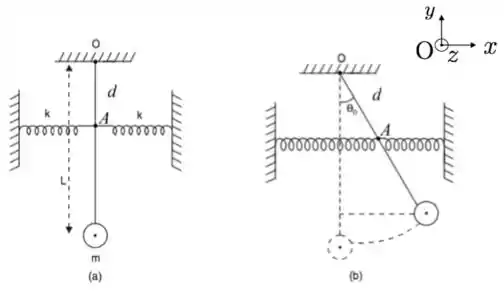
(a) Utilize o sistema de coordenadas da figura e obtenha a equação que descreve o movimento do pêndulo.
(b) Para pequenas oscilações em relação à posição de equilíbrio do pêndulo, determine a freqüência angular de oscilação.
(c) Obtenha a função para pequenas oscilações em relação à posição de equilíbrio.
SUGESTÕES:
• Item (a): Determine o(s) torque(s) em torno ao eixo de rotação ou utilize considerações energéticas.
Ver solução completaQuestão 9
Um haltere de comprimento é formado por uma haste de massa desprezível e duas esferas de massa . O haltere pode girar livremente em torno do ponto , formando um ângulo em relação à horizontal. Uma mola, de constante elástica está conectada a uma distância do ponto e encontra-se relaxada (nem comprimida nem esticada) quando o ângulo é zero. Considerando pequenos valores de , obtenha:
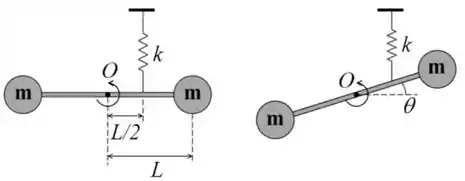
(a) A equação diferencial que rege o comportamento oscilatório do haltere.
(b) A frequência natural de oscilação do haltere. Expresse a resposta em termos de , e .
Ver solução completaQuestão 10
Um pêndulo físico, imerso em um meio viscoso, oscila em torno de um eixo horizontal sob a ação da gravidade e da força de atrito viscoso com uma distância entre o seu centro de massa e o eixo de rotação. No limite de pequenas oscilações, o pêndulo obedece à seguinte equação de movimento:
Sendo . Se necessário, use .
(a) Determine a frequência natural de oscilação () e a constante de amortecimento ().
(b) Determine a solução da equação de movimento para e .
(c) Qual é o tempo necessário para que a amplitude do movimento seja reduzida para um quarto do valor inicial?
Ver solução completaQuestão 11
Uma roda pode girar livremente em torno do seu eixo fixo. Uma mola de constante k é presa a um dos raios a uma distância R do eixo. Suponha que a roda é um anel de massa m e raio R, cujo momento de inércia é igual a .
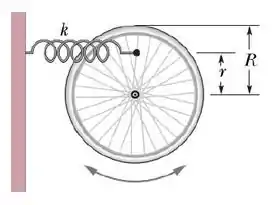
a) Calcule a frequência angular das pequenas oscilações desse sistema, em termos de m, R, r e k.
b) Suponha que o deslocamento angular máximo de um ponto do anel seja e que tem t = 0 s o deslocamento angular desse ponto seja metade desse valor. Escreva a equação do movimento angular do anel.
c) Se o anel tem uma massa m = 3 kg, a constante da mola é k = 100 N/m, = 0,01 rad e , calcule a velocidade angular de um ponto do anel em t = 0 s.
Ver solução completaQuestão 12
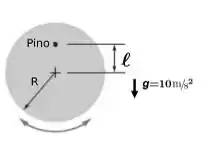
Conforme figura ao lado, um pêndulo é formado por um disco uniforme de massa M sustentado em um plano vertical por um pino situado a uma distância = 3m do centro de massa do disco. O raio do disco é R = 4 m. O pêndulo oscila com uma amplitude angular pequena. Dado que o momento de inércia de um disco homogêneo em relação ao seu centro de massa é , diga qual é a frequência angular de oscilação em rad/s.
a)
b)
c) 2
d)
e)
f)
g)
h)
Ver solução completaQuestão 13
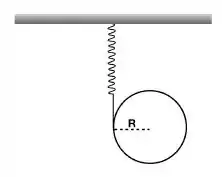
Uma esfera homogênea com 0,5 kg de massa está livre para girar em torno de um eixo vertical que passa pelo seu centro. Uma mola de constante elástica k = N/m é ligada horizontalmente entre a borda da esfera no plano do equador e uma parede fixa. A figura ao lado mostra a vista de topo da esfera e da mola na sua posição de equilíbrio. Determine o período das pequenas oscilações que acontecem quando a esfera é levemente girada no plano do equador e em seguida liberada. Dado:
Questão 14
Uma haste rígida de comprimento e massa está suspensa em um ponto que dista do centro de gravidade da haste. No instante a haste é abandonada a partir do repouso de um ângulo com a direção vertical. Considere o limite de oscilações com ângulos pequenos.
- Obtenha a equação diferencial que descreve o movimento de rotação da haste.
- Determine o período de oscilação da haste nessas circunstâncias.
- Obtenha a solução da equação diferencial.
- Obtenha a energia mecânica da haste no ângulo .
- Determine a razão onde é o período de oscilação quando suspensa por sua extremidade.
Formulário adicional: Momento de inércia de uma barra delgada e uniforme de comprimento e massa em relação a um eixo vertical que passa pelo seu centro:
Ver solução completaQuestão 15
Um pêndulo físico consiste de uma haste rígida delgada, de massa desprezível e comprimento , sobre a qual duas diminutas partículas estão afixadas, uma de massa e outra de massa . As distâncias destas duas massas ao ponto de suspensão são, respectivamente, e . Para pequenas oscilações do pêndulo, podemos afirmar que este desenvolve movimento harmônico, com frequência natural de oscilação:
Questão 16
Um relógio de pêndulo é constituído por uma fina haste de aço de massa unida a um grande disco de bronze de massa . Supondo desprezível qualquer tipo de atrito sobre o pêndulo durante as suas oscilações, analise as afirmativas a seguir:
I - O período desse relógio irá aumentar caso o mesmo seja levado para a superfície da Lua, onde a aceleração da gravidade é menor que a da Terra.
II - Ao aumentarmos a temperatura ambiente de , o período desse relógio irá aumentar.
III - O período desse relógio pode ser calculado pela equação , onde é a distância do centro do disco de bronze ao eixo de oscilação.
São verdadeiras:
- Somente I e II.
- Somente a I.
- Somente II e III.
- Somente I e III.
- Todas.
Questão 17
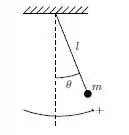
Um pêndulo de comprimento , inicialmente em repouso na sua posição de equilíbrio, recebe um impulso que lhe comunica instantaneamente uma velocidade angular no sentido anti-horário. Seja a frequência angular das oscilações. A função que descreve corretamente seu movimento, supondo pequenas oscilações, é:
Questão 18
(Cap 13 - Ex 45) Uma massa de oscila em uma mola de constante igual a com um período de . Esse sistema é amortecido ou não? Como você sabe disso? Se for amortecido, encontre a constante de amortecimento . Esse sistema é não amortecido, subamortecido, criticamente amortecido ou superamortecido? Como você sabe que é assim?
Ver solução completaQuestão 19
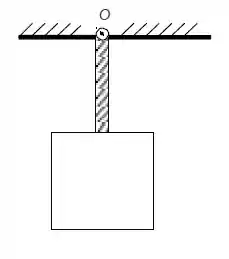
O pêndulo da figura abaixo é formado por uma haste de comprimento e uma chapa quadrada também de lado , presos no ponto de maneira que o conjunto possa se movimentar. Tanto a haste quanto a chapa são uniformes e possuem massa . Os momentos de inércia em torno dos centros de massa de uma haste e de uma chapa quadrada são, respectivamente, e .
- Calcule a distância entre o ponto e o centro de massa desse conjunto .
- Se o pêndulo é posto para oscilar em torno do ponto com ângulo pequeno, qual será o período de oscilação?
Questão 20
O momento de inércia de uma barra uniforme e fina em relação a um eixo perpendicular à barra passando pelo seu centro de massa é , onde é a massa e é o comprimento. Tal barra é suspensa verticalmente por uma de suas extremidades e posta a oscilar a pequenas amplitudes. Se esta barra terá o mesmo período de um pêndulo simples de comprimento:
a)
b)
c)
d)
e)
Ver solução completaQuestão 21
A figura mostra um objeto com forma de estrela, livre para girar ao redor de seu centro de massa e com a ponta superior presa a uma mola. O primeiro gráfico mostra a função [rad, ms] que descreve a posição angular da ponta superior da estrela em função do tempo . O segundo gráfico mostra o torque produzido pela força elástica da mola em função de . A relação entre a deformação do comprimenrto da mola e o ângulo é dada por . A relação entre o torque aplicado à estrela e a força exercida pela mola é dada, para pequenos ângulos, por . Considere .
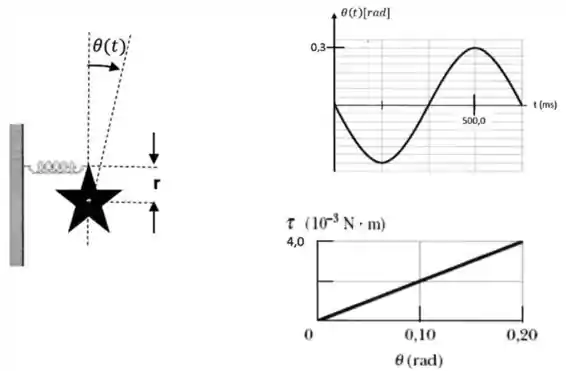
Determine:
(a) a constante elástica da mola.
(b) a frequência angular do MHS resultante.
(c) o momento de inércia da estrela
(d) a constante de fase .
Ver solução completaQuestão 22
Cada um dos dois pêndulos mostrados na figura abaixo consiste em uma esfera sólida uniforme de massa sustentado por uma corda de massa desprezível, porém a esfera do pêndulo é muito pequena, enquanto a esfera do pêndulo é bem maior. Sejam e os tempos que cada pêndulo demora em completar uma oscilação. Para deslocamentos pequenos, pode-se dizer que: Dados: Momento de inércia de uma esfera (a partir de um eixo de simetria): Teorema dos eixos paralelos:
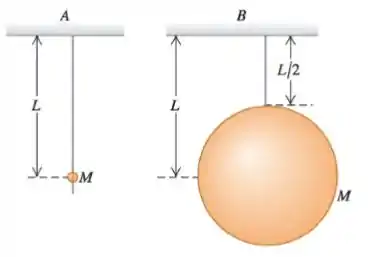
O pêndulo demora mais tempo que o pêndulo em completar uma oscilação, com .
Os dois pêndulos levam o mesmo tempo para completar uma oscilação, com .
O pêndulo demora menos tempo que o pêndulo em completar uma oscilação, com .
O pêndulo demora mais tempo que o pêndulo em completar uma oscilação, com / .
O pêndulo demora menos tempo que o pêndulo em completar uma oscilação, com .
Ver solução completaQuestão 23
Uma bola de aço está pendurada em uma mola ideal vertical e descreve um movimento harmônico simples com uma amplitude de e uma frequência angular de . Qual das expressões abaixo representa a aceleração da bola, em m/s em função do tempo?
a = - 0,157
a = - 0,493 cos (
t
Ver solução completaQuestão 24
Dois pêndulos, cada um composto por um fio de comprimento prendendo uma partícula de massa , realizam um movimento harmônico simples (pequenas amplitudes) com uma mola de constante elástica e massa desprezível unindo as massas no plano de oscilação. Quais o modos normais de oscilação?
- e
- e
- e
- e
- e
Questão 25
Em uma simulação conforme representado pela figura abaixo, a um pêndulo com constante elástica igual a , foi acoplada a uma massa de em sua extremidade, sendo a amplitude de oscilação igual a 0,08 m, podemos afirmar que a energia mecânica do sistema é igual a:
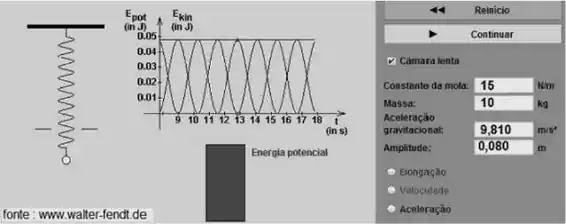
- 0,400J
- 7,928J
- 0,0480J
- 4,80J
- 79,28J
Questão 26
A figura mostra três pêndulos físicos formados por esferas homogêneas iguais, rigidamente
ligadas por barras iguais de massa desprezível. Os pêndulos são verticais e podem oscilar em torno do ponto de suspensão O. Ordene os pêndulos de acordo com o período das oscilações, começando pelo maior.
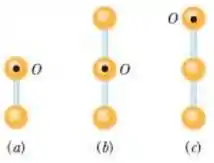
a) a, c, b;
b) b, a, c;
c) b, c, a;
d) c, b, a;
e) todos empatados;
Ver solução completaQuestão 27
Um movimento harmônico simples (MHS) obedece à equação:
- Determine o período de oscilação.
- Se o sistema for um sistema massa mola com a constante elástica da mola igual à , determine a massa do bloco em onças.
- Se o sistema for um pêndulo simples qual o comprimento do fio em metros se a massa for
- Se o sistema for um pêndulo físico associado ao pêndulo simples do item anterior, qual a distância do ponto de suspensão ao centro de oscilação.
Para os itens a seguir considere a condição de pequenas oscilações.
Questão 28
(Cap 13 - Ex 57) Uma força de amortecimento atua sobre um rato infeliz de que se move preso a extremidade de uma mola cuja constante é . Se a constante tem um valor igual a , qual é a frequência de oscilação do rato? Para qual valor da constante o movimento é criticamente amortecido?
Ver solução completaQuestão 29
Uma bolinha homogênea de massa e raio rola sem deslizar sobre uma calha cilíndrica de raio , na vizinhança do fundo, ou seja, na aproximação de ângulos pequenos. Dado
- Faça um esquema das forças que agem sobre a bola e determina a força resultante.
- Escreva e .
- Mostre que o sistema é um oscilador com frequência angular .
- Mostre que a função , onde e são constantes é solução da equação diferencial.
- Considerando que no instante o ângulo é e a velocidade é , determine a solução particular para este oscilador em termos de , , , e .
- Escreva as expressões para e , sendo , a energia potencial e a energia cinética.
- Mostre que é independente do tempo.
Questão 30
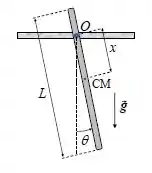
A figura ao lado mostra um pêndulo físico composto por uma barra uniforme de comprimento que pode oscilar livremente em torno de um eixo pelo ponto a uma distância do centro da barra.
- Considere e No instante a barra é abandonada a partir do repouso em um ângulo arbitrariamente pequeno com a vertical. Em segundos, a barra passa pela posição vertical pela primeira vez. Determine o valor de .
- Suponha agora que . Determine, em centímetros, o valor de que minimiza o período.
(Dados:
Questão 31
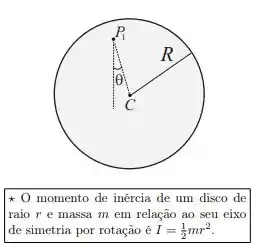
Um pêndulo, constituído por um disco fino de massa e raio , e centro de massa em C, é pendurado por um ponto a uma eixo fixo, conforme mostra a figura. O disco pode balançar livremente, de um lado para outro, quando é deslocado, de um ângulo , a partir de sua posição de equilíbrio. Se o movimento do pêndulo é restringido a ângulos pequenos, e a distância entre o ponto de suspensão e o centro de massa é , o período das oscilações quando ele oscila em torno do ponto é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 32
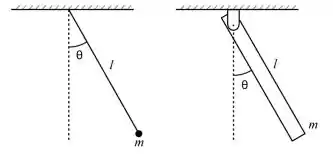
Considere os dois tipos de pêndulos ilustrados ao lado: o primeiro sendo um pêndulo simples e o segundo um pêndulo físico (com momento de inércia igual a em relação à extremidade superior). Julgue as afirmações abaixo, relativas ao movimento de ambos os pêndulos:
) Se considerarmos o regime de oscilações pequenas, ambos os pêndulos descrevem um movimento harmônico simples.
) O período dos dois pêndulos será o mesmo se ambos tiverem a mesma massa e o mesmo comprimento.
) Quanto menor é o ângulo de oscilação de cada pêndulo, menor fica o seu período.
(A) Apenas as afirmações , e estão corretas.
(B) Apenas as afirmações e estão corretas.
(C) Apenas as afirmações e estão corretas.
(D) Apenas a afirmação está correta.
(E) Apenas a afirmação está correta.
Ver solução completaQuestão 33
O pêndulo da figura abaixo é formado por uma haste de comprimento e uma chapa quadrada também de lado , presos no ponto de maneira que o conjunto possa se movimentar. Tanto a haste quanto a chapa são uniformes e possuem massa . Os momentos de inércia em torno dos centros de massa de uma haste e de uma chapa quadrada são, respectivamente, e .
- Calcule a distância entre o ponto e o centro de massa desse conjunto .
- Se o pêndulo é posto para oscilar em torno do ponto com ângulo pequeno, qual será o período de oscilação?
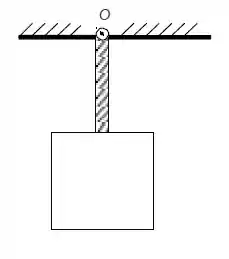
Questão 34
Um pêndulo físico de massa e momento de inércia , está preso em uma de suas extremidades. O pêndulo sofre então uma leve perturbação externa, tal que ele começa a oscilar em pequenos ângulos devido a um campo gravitacional . Assuma também que o centro de massa do pêndulo está a uma distância do ponto fixo. Qual a frequência angular de oscilação?