Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 10.Problemas Adicionais - Ex. 105
105- Existem relatos de guepardos correndo à velocidade impressionante de 114 km/h, feitos por observadores que dirigiam ao lado desses animais. Imagine o que é tentar medir a velocidade de um guepardo mantendo um jipe emparelhado com o animal e ao mesmo tempo olhando de soslaio para um velocímetro que registra 114 km/h. Você conserva o veículo a uma distância constante de 8,0 m do guepardo, mas o barulho do motor faz com que o guepardo se afaste continuamente ao longo de uma trajetória circular com 92 m de raio. Assim, você é forçado a seguir uma trajetória circular com 100 m de raio.
(a) Qual é a velocidade angular (sua e do guepardo) ao longo das trajetórias circulares?
(b) Qual é a velocidade linear do guepardo? (Se você não levasse em consideração o movimento circular, concluiria erroneamente que a velocidade do guepardo era 114 km/h. Aparentemente, esse tipo de erro foi cometido nos relatos publicados.)
Passo 1
Sempre dirijam com segurança!
O que está sendo retratado na questão é o seguinte:
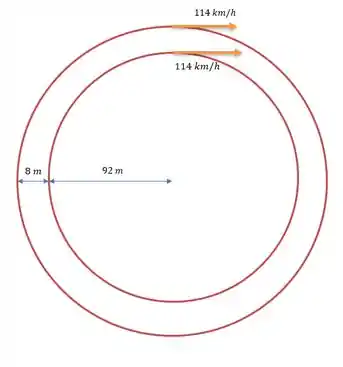
A velocidade angular do carro será de:
Ou a gente trabalho em metros ou em km, poderia muito bem passar o raio para quilômetros. No caso preferi passar a velocidade para metros por segundo.
Passo 2
Como tanto o carro como o guepardo estão em círculos com o mesmo raio, logo os dois estão com a mesma velocidade angular (já que o carro acompanha o guepardo) logo aplicando de novo a fórmula da velocidade angular no círculo do guepardo, nós teremos:
Até dava uma boa aproximação.