Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 9.Problemas Adicionais - Ex. 123
123- Uma sonda espacial não tripulada (de massa m e velocidade v em relação ao Sol) se aproxima do planeta Júpiter (de massa M e velocidade em relação ao Sol), como mostra a Fig. 9-84. A sonda contorna o planeta e passa a se mover no sentido oposto. Qual é a velocidade da sonda, em relação ao Sol, depois do encontro com Júpiter, que pode ser analisado como se fosse uma colisão? Suponha que e (a velocidade orbital de Júpiter). Leve em conta o fato de que a massa de Júpiter é muito maior que a massa da sonda (M ≫ m).
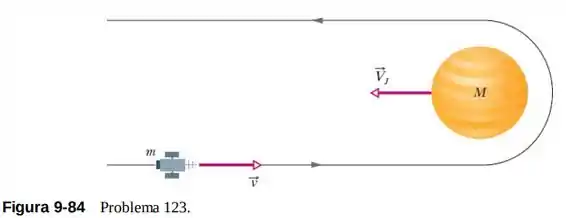
Passo 1
Fazendo o que é proposto no enunciado, vamos fazer a conservação dos momento linear:
Onde é a velocidade da sonda depois da colisão e a velocidade de júpiter depois do sol, e como a massa de júpiter é muito maior que a da sonda ela não afeta seu sentido.
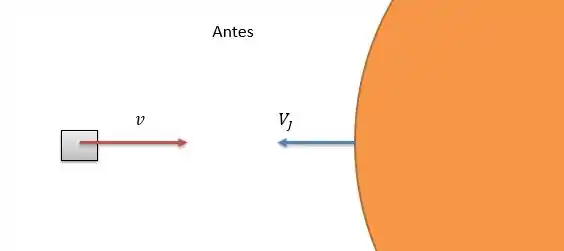
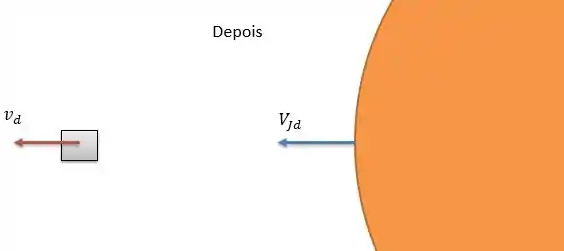
Passo 2
Considerando a colisão perfeitamente elástica, temos a seguinte relação de velocidades de aproximação e afastamento:
Dessa fórmula podemos dizer que:
Logo substituindo na primeira equação:
Isolando :
Como podemos considerar