10.5 Uma força atuando sobre uma peça de uma máquina é dada pela expressão . O vetor da origem ao ponto onde a força é aplicada é dado por a) Faça um diagrama mostrando e a origem. b) Use a regra da mão direita para determinar a direção e o sentido do torque. c) Determine algebricamente o vetor torque produzido por essa força. Verifique se a direção e o sentido do torque são iguais aos obtidos no item (b).
Passo 1
Eaeee, belezinha??? Bom... o enunciado nos diz que uma força atua sobre uma peça de uma máquina de acordo com a seguinte expressão vetorial:
Sabemos também que o vetor da origem ao ponto onde a força é aplicada é dado por:
Queremos fazer um diagrama mostrando os dois vetores e a origem.
Queremos também determinar a direção e o sentido do torque utilizando a regra da mão direita e confirmar esse resultado de forma algébrica.
Para isso, temos que saber da definição de torque :
Onde é a força aplicada e a distância até o ponto.
E seu módulo é:
Agora bora aplicar!! 😉
Passo 2
a)
Vamos começar desenhando esse diagrama. Só lembrando que é o vetor unitário do eixo e é o unitário do eixo .
Como temos que:
Lembrando que indica a distância da origem até o ponto de aplicação da força. E
Isso significa que os dois vetores estão no plano . Então, o diagrama fica da seguinte forma:
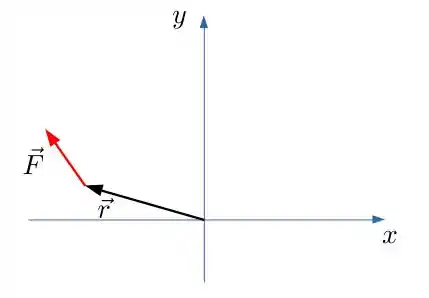
Passo 3
b)
Opa! Vamos olhar o que essa força quer fazer no vetor ! Concorda comigo que essa força ta querendo fazer esse vetor girar no sentido horário?
Para usarmos a regra da mão direita, colocamos nosso dedo indicador na direção no vetor e fechamos a mão na direção no vetor , ao fazer esse giro, o dedo polegar apontará na direção no torque resultante.
Se usarmos a regra da mão direita seguindo esse sentido horário, o nosso polegar aponta pra dentro da página!
Como a direção que entra na direção da página é a direção , então a direção de é ;)
Passo 4
c)
Para interpretar algebricamente o vetor torque produzido pela força, fazemos:
Mas,
Então,
O que concorda com o que dizemos antes, já que apontando na direção significa que o torque aponta para dentro da página! :D
Resposta
a)
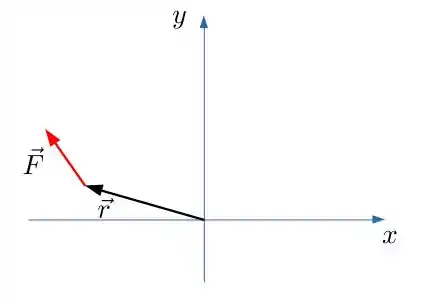
b)
c)