Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.1 - Ex. 4
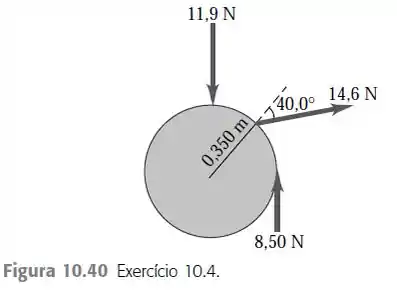
Três forças são aplicadas a uma roda com raio igual a 0,350 m, conforme mostra a Figura 10.40. Uma força é perpendicular à borda, outra é tangente a ela e a outra forma um ângulo
de com o raio. Qual é o torque resultante da roda produzido por essas três forças em relação a um eixo perpendicular à roda e que passa através do seu centro?
Passo 1
Eaee, belezinha??? Bom... temos três forças atuando em uma roda com raio igual a :
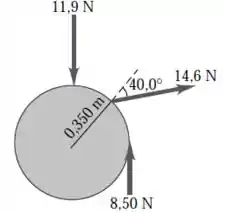
Queremos calcular torque resultante da roda produzido por essas três forças em relação a um eixo perpendicular à roda e que passa através do seu centro.
Para isso, sabemos que a magnitude do torque é dado pelo produto entre a força e o braço de alavanca :
Com .
Para calcular a magnitude de cada torque e usando a regra da mão direita para determinar a direção de cada torque.
E então vamos somar os torques para encontrar o torque total!! 😉
Ah... Vamos considerar que os torques no sentido anti-horário sejam positivos, combinado?? 😉
Passo 2
Para a força
Para a força
e
Para a força
e
Passo 3
Então, pelo conceito de torque, temos:
E
E
Passo 4
E então, para calcularmos o adicionamos todos os torques calculados:
Isso implica que:
O torque líquido é e é no sentido horário.
Resposta
O torque líquido é e é no sentido horário.