Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Exercício - Ex. 38
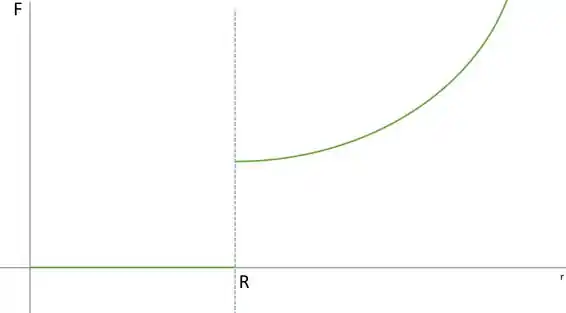
12.38. Uma casca esférica, uniforme, de massa igual a 1000 kg, possui um raio de 5,0 m. (a) Ache a força gravitacional que essa casa exerce sobre uma massa pontual de 2,0 kg colocada nas seguintes distâncias do centro da casca: (i) 5,01 m, (ii) 4,99 m, (iii) 2,72 m. (b) Desenhe um gráfico qualitativo do módulo da força gravitacional que essa esfera exerce sobre uma massa pontual m em função da distância r de m do centro da esfera. Inclua a região de r=0 a
Passo 1
Vamos começar resolvendo o item (a). Bom a esfera tem e no caso (i), a massa pontual está a uma distância , então , logo, existe uma força gravitacional agindo sobre as massas. Essa força gravitacional pode ser calculada como se calcula duas massas pontuais a uma distância
Agora é só substituir os valores
Fazendo essa continha
Passo 2
Agora vamos calcular para o caso (ii). Bem agora , então , e como estamos falando só de uma casca esférica, a gente conclui que a massa pontual está dentro da casca esférica. Nesse caso não a força gravitacional entre as duas massas.
O caso (iii) é muito semelhante, porque , e consequentemente , e assim não há força gravitacional.
Passo 3
Agora para desenhar o gráfico de forma qualitativa, a gente tem que notar que o módulo da força é 0 quando e é maior que 0 quando , e no ponto , temos
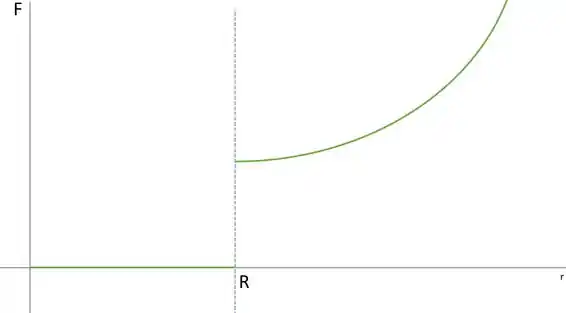
Resposta
b)
