Exercícios de Aceleração da gravidade no interior de cascas e esferas - Lista de Exercícios Resolvida
Questão 1
Explique por que o campo gravitacional dentro de uma esfera maciça de massa homogênea é diretamente proporcional a e não inversamente proporcional a .
Ver solução completaQuestão 2
Uma casca esférica fina e homogênea tem de raio e de massa, e seu centro está localizado na origem de um sistema de coordenadas. Outra casca esférica fina e homogênea, com de raio e de massa, está dentro da casca maior, com seu centro em no eixo . Qual é a força gravitacional de atração entre as duas cascas?
Ver solução completaQuestão 3
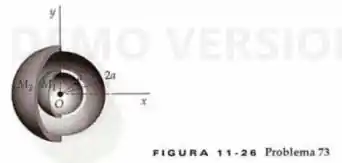
Duas cascas esféricas finas, homogêneas e concêntricas, possuem massas e e raios e , como na Figura 11-26. Qual é a magnitude da força gravitacional sobre uma partícula pontual de massa (não mostrada) localizada (a) a uma distância do centro das cascas? (b) a uma distância do centro das cascas? (c) a uma distância do centro das cascas?
Questão 4
Uma casca esférica, uniforme, de massa igual a , possui um raio de . (a) Ache a força gravitacional que essa casca exerce sobre uma massa pontual de colocada nas seguintes distâncias do centro da casca: (i) , (ii) , (iii) . (b) Desenhe um gráfico qualitativo do módulo da força gravitacional que essa esfera exerce sobre uma massa pontual em função da distância de do centro da esfera. Inclua a região de a .
Ver solução completaQuestão 5
A uma profundidade igual à metada do raio da Terra, a aceleração da gravidade vale cerca de:
- Não se pode determinar a resposta com os dados fornecidos
Questão 6
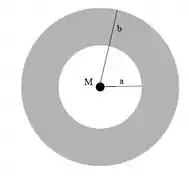
A figura ao lado ilustra uma sistema composto por 2 massas. A localizada na origem é uma massa pontual de massa M, a outra é uma casca esférica espessa centrada na origem, onde a é seu raio interno e b o raio externo. A casca possui densidade de massa uniforme . Uma partícula de prova de massa m é colocada em 2 regiões distintas no espaço, e . Assinale abaixo a alternativa que contém o módulo da força gravitacional resultante correta sobre a partícula de prova nas regiões e respectivamente.
a) e
b) e
c) e
d) e
e) 0 e
f) 0 e
Ver solução completaQuestão 7
Uma camada esférica tem raio interno , raio externo e uma massa , uniformemente distribuída pela camada. A força gravitacional exercida sobre a camada por uma massa puntiforme colocada a uma distância do centro, com , é:
a)
b)
c)
d) zero
e)
Ver solução completaQuestão 8
Uma esfera homogênea feita de poeira (podemos penetrá-la) tem massa e raio . Sendo a constante gravitacional de Newton, qual é o módulo da aceleração que uma partícula pontual localizada a uma distância do centro da esfera sentirá por conta da atração gravitacional da esfera?
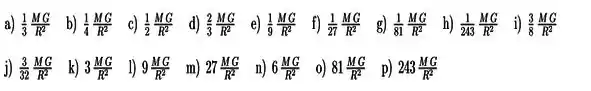
Questão 9
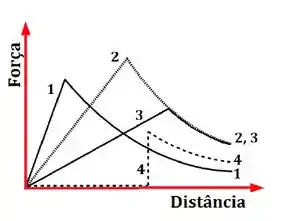
O gráfico ao lado mostra a força de atração exercida por quatro objetos esféricos distintos (objetos 1, 2, 3 e 4) sobre um mesmo corpo de prova em função da distância desse corpo até o centro de cada um dos objetos. Os gráficos englobam as regiões interiores e exteriores desses objetos. Marque a alternativa abaixo que não estão de acordo com o que é mostrado no gráfico.
(a) O raio do objeto 3 é maior que o do objeto 2.
(b) O objeto 4 é uma casca esférica.
(c) O objeto 1 é uma esfera maciça e de densidade homogênea.
(d) Os objetos 2 e 3 têm a mesma massa.
(e) A densidade do objeto 2 é maior que a densidade do objeto 1.
(f) A massa do objeto 4 é maior que a massa do objeto 1.
Questão 10
Uma partícula de massa encontra-se a uma distância do centro de uma distribuição esferossimétrica de massa. Essa distribuição consiste de uma massa uniforme sobre uma casca esférica de raio , concêntrica com outra massa uniforme em uma esfera maciça de raio . Seja o módulo da força gravitacional sobre . Que gráfico representa a razão , como função de ?
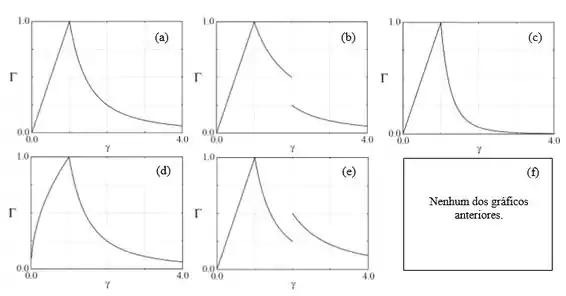
Questão 11
3 – Um planeta é modelado por um núcleo de raio e massa cercado por uma casca de raio interno , raio externo e massa . Se e , qual é a aceleração gravitacional de uma partícula em pontos situados a uma distância (a) e (b) do centro do planeta?
Ver solução completa