Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 107

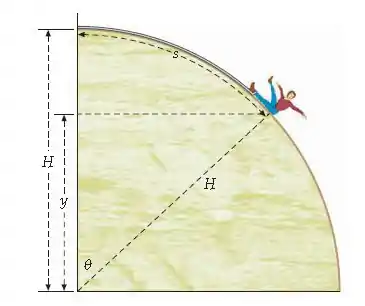
Um praticante de rapel desce uma face de um penhasco quando tropeça e começa a deslizar sobre a rocha, preso apenas à corda de b u n g e e - j u m p que está presa no topo do penhasco. A face do penhasco tem a forma de um suave quadrante de cilindro, de altura (e raio) H = 300   m (Figura 7-58). Trate a corda de b u n g e e - j u m p como uma mola de constante de força k = 5,00   N / m e comprimento frouxo L = 60,0   m . A massa do montanhista é 85,0   k g . (a) Usando um programa de planilha eletrônica, faça um gráfico da energia pontencial do montanhista como função de s , sua distância ao topo do penhasco m e d i d a   a o   l o n g o   d a   s u p e r f í c i e   c u r v a . Use valores de s entre 60,0   m e 200   m . (b) A queda começou quando o montanhista estava a uma distância s i = 60,0   m do topo do penhasco e terminou quando ele estava a uma distância s f = 110   m do topo. Determine a energia dissipada pelo atrito entre o momento do tropeço e o momento em que ele parou.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom, precisamos calcular a energia potencial total. Ela é dada pela soma entre a energia potencial do bungee jump e a energia potencial gravitacional. Temos que:

U s = U b j + U g

Como a corda do bungee jump é tratada como uma mola, temos que:

U b j = 1 2 k s - L 2

A Energia potencial gravitacional é dada por:

U g = M g y = M g H cos ⁡ θ

U g = M g H cos ⁡ s H

Substituindo, temos:

U s = 1 2 k s - L 2 + M g H cos ⁡ s H

Esta fórmula será a utilizada na planilha e iremos variar os valores de s .

Abaixo está a figura da planilha onde podemos ver o comportamento da Energia Potencial ao variarmos s .

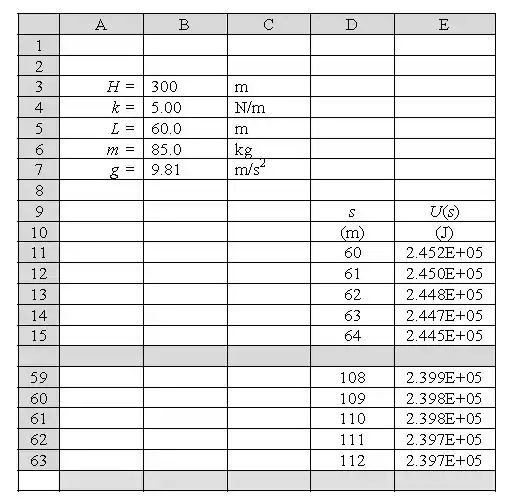
A partir dos dados, foi possível plotar o seguinte gráfico:

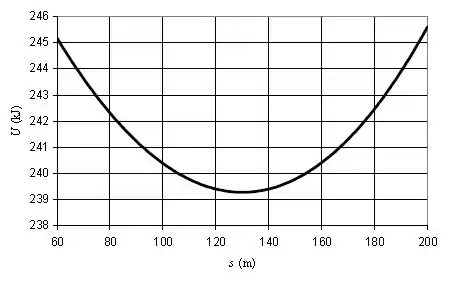
Passo 2

Item (b):

Aplicando o teorema do trabalho energia, temos que:

W e x t = ∆ K + ∆ U s + ∆ E t é r m

Sabemos que não existe influência de trabalho externo nem parcela cinética, portanto:

∆ U s + ∆ E t é r m = 0

Temos que:

∆ U s = - ∆ E t é r m

Substituindo os pontos de interesse, temos:

U 110   m - U 60   m = - ∆ E t é r m

∆ E t é r m = - U 110   m + U 60   m

∆ E t é r m = - 1 2 k 110 - L 2 + M g H cos ⁡ 110 H + 1 2 k 60 - L 2 + M g H cos ⁡ 60 H

∆ E t é r m = - 1 2 k 110 - L 2 - 60 - L 2 - M g H cos ⁡ 110 H - cos ⁡ 60 H

Substituindo os valores, temos:

∆ E t é r m = - 1 2 5 110 - 60 2 - 60 - 60 2 - 85 ⋅ 9,81 ⋅ 300 cos ⁡ 110 300 - cos ⁡ 60 300

∆ E t é r m = - 1 2 5 50 2 - 0 2 - 85 ⋅ 9,81 ⋅ 300 cos ⁡ 110 300 - cos ⁡ 60 300

∆ E t é r m = 5392   J

Nos cálculos fique atento, pois o cosseno deve ser calculado em radianos.

Resposta

b ) ∆ E t é r m = 5392   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pêndulo é formado por uma pedra de 2,0k g oscilando na extremidade de uma corda de 4,0m de comprimento e massa desprezível. A pedra tem uma velocidade de 8,0m / s ao passar pelo ponto mais baixo da
A Fig. 8-32 mostra um pêndulo de comprimento L = 1,25m . O peso do pêndulo (no qual está concentrada, para efeitos práticos, toda a massa) tem velocidade v 0 quando a corda faz um ângulo θ 0 = 40,0 °
Um pêndulo consiste em uma pequena bola de massa m presa a um fio de comprimento L . A bola é segurada lateralmente com o fio na horizontal (Figura 7-56). Então ela é largada do repouso. No ponto mais
Um professor de colégio sugeriu, certa vez, o seguinte método para medir a magnitude da aceleração de queda livre: pendure uma massa em um fio bem fino (comprimento L ) para fazer um pêndulo com a mas