Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 8.Problemas Adicionais - Ex. 135

135- Repita o Problema 83 supondo que o bloco está subindo uma rampa que faz um ângulo de 5,0° com a horizontal.

Passo 1

Dados da questão 83-

Massa= 15   k g

Aceleração = 2   m / s 2

Não existe atrito

Velocidade inicial= 10   m / s

Velocidade final = 30   m / s

  1. Variação da energia mecânica no bloco.
  2. Taxa de transferência de energia para o bloco
  3. Taxa instantânea de energia quando a velocidade é de 10
  4. Taxa instantânea de energia quando a velocidade é de 30

Passo 2

  1. Representando o plano inclinado descrito nós teremos:

Por Torricelli conseguimos encontrar a variação de distância no plano entre os blocos, logo:

v f 2 = v 0 2 + 2 a Δ s

Substituindo os valores temos:

30 2 = 10 2 + 2 × 2 Δ s → Δ s = 200   m

Logo Δ h poderá ser:

sin ⁡ 5 = Δ h Δ s → Δ h = 200 sin ⁡ 5 = 17.43   m

Passo 3

  1. A energia mecânica do bloco sobe pela energia cinética e a energia potencial gravitacional.

A energia cinética inicial é de:

K 0 = 1 2 × 15 × 10 2 = 750   J

Já a energia depois será a variação da altura mais a energia cinética no instante.

E m f = 1 2 × 15 × 30 2 + 15 × 9.81 × 17.43 = 9314.82   J

Logo a variação será:

Δ E m = 9314.82 - 750 = 8564.82   J

Passo 4

Taxa de transferência de energia, é sempre o quanto de energia se passa ao sistema por tempo, isso é a potência!

E para fazer a potência precisamos encontrar o tempo, uma vez que a diferença de energia já foi descoberta.

Fazendo a equação:

v f = v 0 + a t

Conseguimos descobrir esse tempo:

30 = 10 + 2 t → t = 10   s

Fazendo a potência:

P = E t = 8564.82 10 = 856.48   W

Passo 5

Para calcular a potência instantânea não podemos calcular ela pelo tempo, tendo que saber uma outra opção para tal, uma boa é a fórmula:

P = F v

Onde F será a força paralela a rampa, tal como no cálculo do trabalho. A potência na verdade é a derivada no tempo do trabalho então elas são da mesma família.

Analisando o sistema de forças do bloco no plano inclinado temos:

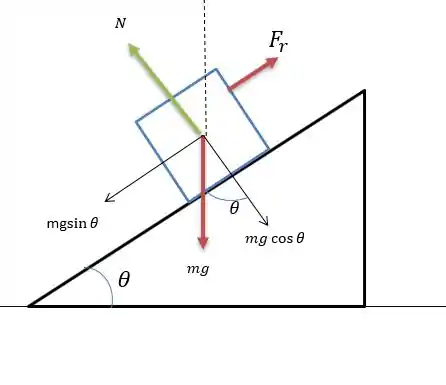
Onde temos uma força resultante capaz de vencer a força m g sin ⁡ θ que desce a rampa e ainda imprime uma aceleração de 2   m / s 2 , logo:

F r = m g sin ⁡ θ + m a = 15 × 9.81 sin ⁡ 5 + 15 × 2 = 42.8   N

c)Para a velocidade de 10   m / s a potência será:

P = 42.8 × 10 = 428   W

d)Para a velocidade de 30   m / s a potência será de:

P = 42.8 × 30 = 1284   W

Resposta

a )   8564.82   J

b )   856.48   W

c )   428   W

d ) 1284   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

53 . Uma batata de 0,300k g é presa a um barbante com comprimento de 2,50m , e a outra ponta do barbante é presa a um suporte rígido. A batata é alinhada horizontalmente a partir do ponto de suporte,
Dois corpos são conectados por um barbante leve que passa sobre uma roldana leve e sem atrito, como mostrado na Figura P7.7. O corpo de massa m1 é solto do repouso a uma altura h acima da mesa. Usando
O sistema mostrado na Figura P7.9 consiste em uma corda leve, não extensível, roldanas leves e sem atrito e blocos de massa igual. Note que o bloco B está preso a uma das roldanas. O sistema é inicial
Revisão. Uma conta desliza sem atrito numa rampa contendo um giro (looping) (Fig. P7.3). A conta é liberada do repouso a uma altura h = 3,50R. (a) Qual é sua velocidade no ponto A? (b) Que intensidade
Dois corpos são conectados por um barbante leve que passa sobre uma roldana leve e sem atrito, como mostrado na Figura P7.7. O corpo de massa m1 = 5,00 kg é solto do repouso a uma altura h = 4,00 m ac