Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 12.Exercícios - Ex. 10

As massas pontuais m e 2 m estão situadas ao longo do eixo x , com m na origem e 2 m   em x   =   L . Uma terceira massa pontual M é deslocada ao longo do eixo x. (a) Em que ponto a força gravitacional resultante sobre M em virtude das duas outras massas é igual a zero? (b) Desenhe o componente x da força resultante sobre M em virtude de m   e   2 m , supondo que as grandezas à direita sejam positivas. Inclua as regiões x <   O ,   O < x < L   e   x >   L . Não deixe de mostrar o comportamento do gráfico em ambos os lados de x = O e x = L .

Passo 1

Faaaaala meu povo, bora iniciar mais um livrinho com a gente!

Letra a)

Bem galera, para resolver esta parte, lembre-se de que a massa M está localizada entre as massas m e 2 m no eixo x. A adição da influência gravitacional de m em M e 2 m em M é zero. Resolveremos a distância x da massa m na origem em termos do comprimento entre as duas massas, L .

- G ( m ) ( M ) x 2 + G ( 2 m ) ( M ) L - x 2 = 0  

G ( 2 m ) ( M ) L - x 2 =   G ( m ) ( M ) x 2

Dividindo ambos os lados da equação por G ( m ) ( M ) , temos:

2 L - x 2 =   1 x 2

2 x 2 = L - x 2

Tirando a raiz quadrada de ambos os lados da equação, teremos:

2 x = L - x

2 x + x = L

x ( 2 + 1 ) = L

Resolvendo para x , encontramos:

x = L 2 + 1

x = 1 2 + 1 × L

x = 0,414   L

Passo 2

Letra b)

Uma dica para esse item é ao esboçar a componente x da força, não se esqueça de que a força muda de sinal dependendo de onde a massa M está.

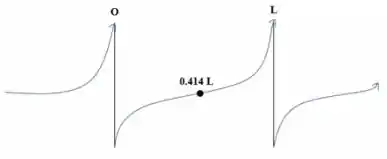
Olhando para a imagem acima, podemos concluir algumas coisas:

Objetos na realidade não são massas pontuais, então não é possível ter m e M exatamente em x = 0 ou 2 m e M em x = L .

Dado que as forças gravitacionais entre dois objetos se aproximam do infinito à medida que se aproximam cada vez mais, a imagem reflete isso com precisão.

Tudo certinho? Te vejo na próximaaaaa!

Resposta

Letra a)

x = 0,414   L

Letra b)

V e r   p a s s o   a   p a s s o

Exercícios de Livros Relacionados

11.4P A aceleração aparente (aceleração dos corpos em queda livre) da gravidade ao nível do mar na linha do equador é 9,78039m/s² ². Entretanto, este valor é menor do que a gravidade real g r , pois d
11.1E Na experiência de Cavendish (ver Figura 11.1), M = 10 kg e m = 10g , e a distância entre o centro de cada esfera pequena e sua esfera grande vizinha é 5cm . A distância entre os centros das esfe
11.22E Calcule a diferença ∆ g da gravidade da Terra nas duas faces opostas da Lua.
11.7E Calcule a força de atração e a energia potencial entre o Sol e Terra, sabendo-se que a distância entre eles é r = 1,50 × 10 11m e que suas massas são M S = 1,99 × 10 30kg , M T = 5,97 × 10 24kg
Um estudante escreveu: “A única razão pela qual a maçã cai no sentido da Terra em vez de a Terra subir no sentido da maçã é que a massa da Terra é muito maior que a massa da maçã e, portanto, ela exer