Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.5 - Ex. 28
Uma caixa de pão de sobre um plano inclinado sem atrito de ângulo está presa, por uma corda que passa por uma polia, a uma mola de constante elástica , como mostra a Fig. 8-41. A caixa é liberada a partir do repouso quando a mola se encontra relaxada. Suponha que a massa e o atrito da polia sejam desprezíveis. (a) Qual a velocidade da caixa após percorrer ? (b) Que distância o bloco percorre do ponto em que foi liberado até o ponto em que para momentaneamente e quais são (c) o módulo e (d) o sentido (para cima ou para baixo ao longo do plano) da aceleração do bloco no instante em que para momentaneamente?
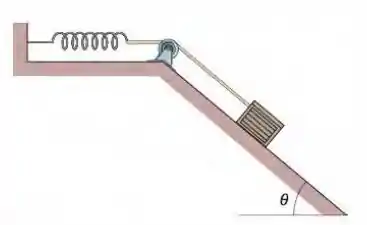
Figura 8-41 Problema 30
Passo 1
a) Tomemos a posição 1 como a altura inicial da caixa e o ponto 2, a altura da caixa quando ela percorre uma distância . Além disso, utilizaremos o ponto 1 como referência.
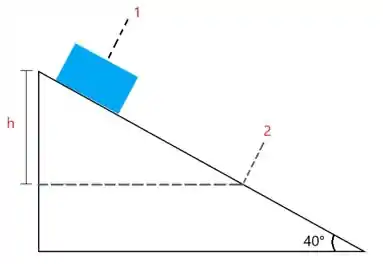
A altura do ponto 2 será dado por .
No ponto 1, energia cinética igual a zero (caixa em repouso) e energia potencial igual a zero (mola relaxada). No ponto 2, temos energia cinética, potencial elástica e potencial gravitacional. Logo , pelo princípio da conservação entre os pontos 1 e 2, temos
Para um deslocamento , ,, ,
Passo 2
b) No ponto em que a caixa para momentaneamente (), temos
Com
Passo 3
No instante em que a caixa encontra-se parado, temos a força elástica da mola () para cima e componente x da gravidade () que age sobre a caixa para baixo. Assim a Força resultante será
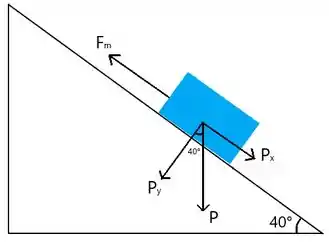
A força é dada por
Logo a aceleração será
c) Dessa forma, o módulo da aceleração é
Passo 4
d) E o seu sentido é contrário ao movimento, logo seu sentido é Para cima.
Resposta
a)
b)
c)
d) Para cima