Na Fig. 8-40, um bloco de massa é liberado a partir do repouso em um plano inclinado sem atrito de ângulo . Abaixo do bloco há uma mola que pode ser comprimida por uma força de . O bloco para momentaneamente após comprimir a mola . (a) Que distância o bloco desce ao longo do plano da posição de repouso inicial até o ponto em que para momentaneamente? (b) Qual é a velocidade do bloco no momento em que entra em contato com a mola?

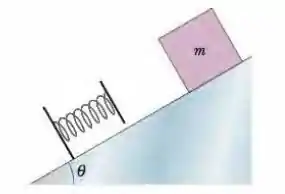
Figura 8-40 Problema 29

Temos 3 pontos principais: 1 – bloco inicialmente em repouso; 2 – bloco entra em contato com a mola; 3 – bloco comprime a mola e para momentaneamente, como mostrado na Figura abaixo.

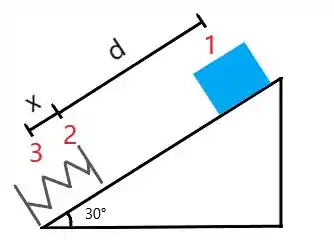
a) Como uma força de é capaz de comprimir a mola em , sua constante elástica () será

A distância entre os pontos 1 e 3 é dada por . Essa distância está relacionada com a altura por meio da inclinação do plano por meio da equação abaixo

No ponto 1, tem-se apenas a energia potencial gravitacional, uma vez que o bloco encontra-se em repouso. Já no ponto 3, o bloco possui apenas a energia potencial elástica, pois ele para momentaneamente. Dessa forma, pelo princípio de conservação da energia mecânica

Colocando em evidência

Para , , e

Assim, a distância total percorrida será