131- Prenda uma das extremidades de uma mola vertical no teto, prenda um repolho na outra extremidade e baixe o repolho lentamente até que a força para cima exercida pela mola sobre o repolho equilibre a força gravitacional que atua sobre ele. Mostre que a perda de energia potencial gravitacional do sistema repolho-Terra é igual a duas vezes o ganho de energia potencial da mola. Por que as duas grandezas não são iguais?
Passo 1
Vamos desenhar o nosso sistema com o repolho:
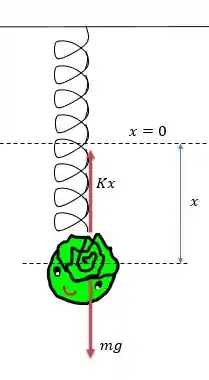
Considerando como o alongamento da mola temos como posição de equilíbrio desse sistema.
Passo 2
A somatória de energias nesse sistema pode ser considerada igual a:
Onde é a energia potencial elástica e a energia potencial gravitacional.
Já a perda de energia gravitacional vale:
E a energia potencial elástica:
Com isso vemos que:
Passo 3
As duas energias não são iguais pois o repolho foi descida lentamente até a posição de equilíbrio da mola, isso faz com que tenha sido aplicada para cima para compensar essa força peso do repolho (com a mão tentando segurar esse repolho) se não fosse essa força a mola e o repolho estariam em sistema harmônico produzindo uma oscilação em torno desse ponto de equilíbrio. Se não existir atrito no sistema o sistema oscilaria pra sempre.
Resposta
Ei, a resposta está no passo a passo :)