Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.5 - Ex. 33

Na Fig. 8-44, uma mola com k = 170   N / m está presa no alto de um plano inclinado sem atrito de ângulo θ = 37,0 ° . A extremidade inferior do plano inclinado está a uma distância D = 1,00   m da extremidade da mola, a qual se encontra relaxada. Uma lata de 2,00   k g é empurrada contra a mola até a mola ser comprimida 0,200   m e depois liberada a partir do repouso. (a) Qual é a velocidade da lata no instante em que a mola retorna ao comprimento relaxado (que é o momento em que a lata perde contato com a mola)? (b) Qual é a velocidade da lata ao atingir a extremidade inferior do plano inclinado?

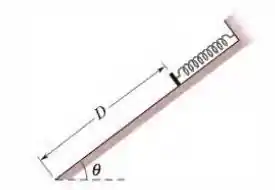
Figura 8-44 Problema 33

Passo 1

a) Primeiro tomemos a base do plano como nosso referencial para o cálculo da energia potencial gravitacional.

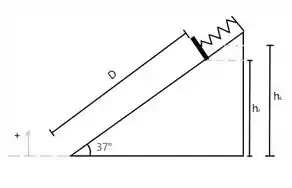
A altura da mola relaxada ( h r ) é dada por

s e n θ = h r D

h r = D s e n θ

E para a altura da mola comprimida ( h c )

s e n θ = h c D + x

h c = D + x s e n θ

Aplicando a lei de conservação de energia para os pontos onde a mola está comprimida e para a mola relaxada, temos

U e c + U g c = K r + U g r

1 2 k x 2 + m g h c = 1 2 m v 2 - m g h r

1 2 m v 2 = 1 2 k x 2 + m g h c - m g h r

Multiplicando toda a equação por 2 m

v 2 = k x 2 m + 2 g h c - 2 g h r

v 2 = k x 2 m + 2 g h c - h r

v 2 = k x 2 m + 2 g D + x s e n θ - D s e n θ

v 2 = k x 2 m + 2 g x s e n θ

v = k x 2 m + 2 g x s e n θ

Para k = 170   N / m , x = 0,200   m , m = 2,0   k g , g = 9,81   m / s 2 e θ = 37,0 °

v = 170.0,2 2 2 + 2.9,81.0,2 . s e n 37 °

v = 2,4   m / s  

Passo 2

b) Pela Lei de conservação de energia entre o ponto da mola comprimida e a base do plano inclinado, temos

U g c + U e c = K b

m g h c + k x 2 2 = m v 2 2

Multiplicando toda a equação por 2 m

v b 2 = 2 g h c + k x 2 m

v b = 2 g D + x s e n θ + k x 2 m

Para D = 1,00   m

v b = 2.9,81 1 + 0,2 s e n 37 ° + 170.0,2 2 2

v b = 4,19   m / s  

Resposta

a)   v = 2,4   m / s  

b)   v b = 4,19   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 8-34 mostra uma pedra de 8,00k g em repouso sobre uma mola. A mola é comprimida 10,0c m pela pedra. (a) Qual é a constante elástica da mola? (b) A pedra é empurrada mais 30c m para baixo e libe
Uma bola de gude de 5,0g é lançada verticalmente para cima usando uma espingarda de mola. A mola deve ser comprimida de exatamente 8,0c m para que a bola alcance um alvo colocado 20m acima da posição
Um bloco de 700g é liberado a partir do repouso de uma altura h 0 acima de uma mola vertical com constante elástica k = 400N / m e massa desprezível. O bloco se choca com a mola e para momentaneamente
Um bloco de 20k g sobre uma superfície horizontal está preso a uma mola horizontal de constante elástica k = 4,0k N / m . O bloco é puxado para a direita até a mola ficar distendida 10c m em relação a
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d