Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 8.Problemas Adicionais - Ex. 133
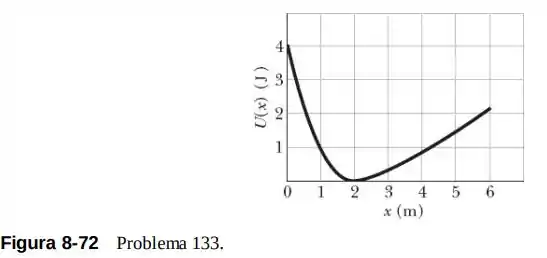
133- Uma força conservativa age sobre uma partícula que se move ao longo de um eixo x. A Fig. 8- 72 mostra a variação da energia potencial associada a com a posição da partícula.
(a) Plote F(x) no intervalo 0
(b) Se a energia mecânica E do sistema é 4,0 J, plote a energia cinética K(x) da partícula no gráfico da Fig. 8-72.
Passo 1
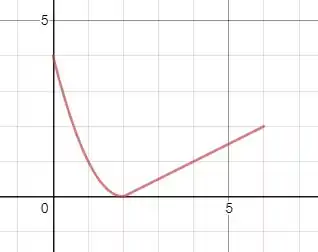
Para fins de aproximação vamos aproximar o gráfico de para uma parábola que vai de até uma reta que vai de até .
Como precisamos de três pontos para encontrar uma parábola podemos pegar os pontos , e e se substituirmos na equação genérica de uma parábola.
Nós encontraremos:
Já para a reta podemos pegar os pontos e com isso encontraremos a reta:
Isso nos dará uma curva bem próxima se respeitarmos os limites de para essas duas funções.
Passo 2
Agora para encontrar o gráfico basta aplicar a seguinte teoria:
Com isso temos que no intervalo de temos a seguinte equação de modelo para :
Já para o intervalo de teremos:
Isso nos dará o seguinte modelo de :
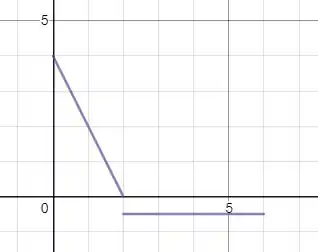
Basta ligar as duas retas e embarrigar as duas retas para conseguir uma resposta mais exata. Mas ela decresce antes de e tende a ser constante depois.
Passo 3
b) Como nos foi fornecida a energia mecânica basta fazermos:
Plotando esse gráfico temos:
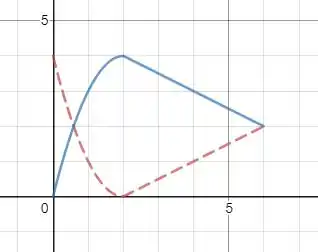
Onde é a curva azul
Resposta
Ei, a resposta está no passo a passo :)