Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 7.Problemas - Ex. 77
Você está projetando um pêndulo para uma feira de ciências. O pêndulo é feito a partir da conexão de uma esfera de bronze com massa m à ponta inferior de um longo fio de metal leve de comprimento (desconhecido) . Um dispositivo próximo ao topo do fio mede a tensão no fio e a transmite para seu notebook. Quando o fio está na vertical e a esfera está em repouso, o centro da esfera está acima do piso e a tensão no fio é igual a . Mantendo o fio esticado, você puxa a esfera para um lado (usando uma escada, se for preciso) e o solta suavemente. Você registra a altura do centro da esfera a partir do piso no ponto onde a esfera foi liberada e a tensão no fio à medida que a esfera passa por seu ponto mais baixo. Os resultados são estes:
Suponha que a esfera possa ser tratada como uma massa pontual, ignore a massa do fio e considere que a energia mecânica é conservada durante cada medição. Desenhe o gráfico de em função de e use-o para calcular . Se a resistência de ruptura do fio for , de que altura máxima a esfera pode ser liberada se a tensão no fio não puder ultrapassar metade da resistência de ruptura? O pêndulo está balançando quando você saiu ao final do dia. Você tranca as portas do local e ninguém entra no prédio até que você retorne na manhã seguinte. Você encontra a esfera pendurada em repouso. Usando as considerações de energia, como poderia explicar esse comportamento?
Passo 1
Vem comigo que essa questão vai ser dominada!
O que temos aqui acaba sendo um caso de pêndulo simples onde temos a conservação de energia.
Para encontrar o comprimento pedido no item vamos usar a conservação de energia, onde vamos considerar o momento inicial quando a esfera é solta e o momento final quando ela passa pelo ponto mais baixo.
E vamos usar a segunda lei de Newton, já que a força resultante nesse caso é a força centrípeta e ela depende de .
Para achar a altura que a bola pode ser solta e que não ultrapasse a tensão de (metade da resistência de ruptura) vamos usar a expressão para que podemos encontrar usando a segunda lei de Newton.
Vamos nessa então!
Passo 2
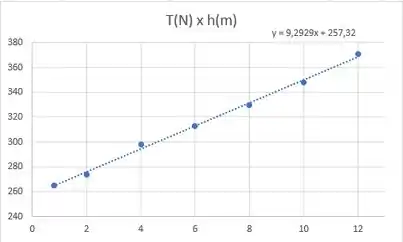
O grafico de em função de é mostrado abaixo.
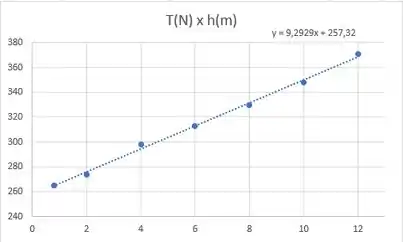
Agora usando a conservação de energia temos:
Onde nesse caso teremos , assim:
Aplicando a segunda lei de Newton para o pêndulo na posição mais baixa, temos:
Passo 3
Substituindo essa última equação na equação que chegamos da conservação de energia, temos:
Agora vamos isolar , temos:
Agora se compararmos essa equação com a equação do gráfico, podemos ver que é o e o é o , então:
Passo 4
O enunciado fala que a tensão do fio quando ele está na vertical e parado é igual a , quando ele está nessa situação temos que:
Logo:
Então temos que:
Passo 5
Agora para a letra .
Através da segunda lei de Newton e da conservação de energia, chegamos em:
Da equação do gráfico podemos tirar que:
Então:
Queremos saber o valore de para que seja igual a , assim:
Essa é a altura máxima pedida em
Passo 6
Agora o último item! O item .
O fato do pêndulo parar acontece pela perda de energia que ele sofre devido ao atrito com o ar (já que o atrito é uma força dissipativa) e o atrito no suporte onde ele oscila.
Resposta
Explicado acima.