Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 7.Problemas - Ex. 71
Um pequeno bloco com massa de desliza em um círculo vertical de raio no interior de uma pista circular. Não há atrito entre a pista e o bloco. Na parte inferior de sua trajetória, a força normal exercida pela pista sobre o bloco tem módulo de . Qual é o módulo da força normal que a pista exerce sobre o bloco quando ele está
no topo de sua trajetória?
Passo 1
Vem comigo que a gente se livra dessa juntos!
A trajetória que bloco segue é bem dizer essa aqui:
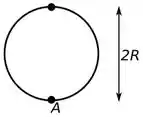
Para encontrar a força norma no ponto mais alto da trajetória vamos usar a segunda lei de Newton ao nosso favor.
Lembrando que a força resultante sobre o bloco é igual a força centrípeta por conta do movimento circular.
E as únicas forças que agem sobre o carrinho na vertical é a força normal e a força peso.
Mas para seguir nesse caminho temos que conhecer a velocidade do bloco no ponto mais alto, já que a força centrípeta depende da velocidade.
Vamos então usar a conservação de energia para achar essa velocidade, temos que:
Considerando o ponto como sendo o ponto onde temos o zero de energia potencial gravitacional, ficamos com:
Mas para essa conta precisamos conhecer a velocidade do bloco em e para isso vamos usar a segunda lei de Newton ao nosso favor aqui também.
Passo 2
Vamos primeiro encontrar a velocidade no ponto , usando a segunda lei de Newton, temos:
Isolando , temos:
Substituindo os valores que conhecemos, temos:
Passo 3
Agora que temos a velocidade em , podemos calcular a velocidade em . Temos:
Substituindo os valores que temos, ficamos com:
Passo 4
Agora podemos calcular a força normal no ponto mais alto. Usando a segunda lei de Newton:
Isolando , temos:
Substituindo os valores que temos, ficamos com:
Com isso temos que:
Essa é a normal sobre o carrinho no ponto mais alto!